Physics Laboratory Experiment on Acceleration Report

Introduction

The purpose of the experiment was to study the relationship that exists between an object using a uniform circular motion to move and the force that is required to cause that acceleration. The conical pendulum was used to examine the mathematics and physics associated with uniform circular motion (Minkin, L., & Sikes, 2021). The conical pendulum moves at a constant spend in a circular horizontal plane and when the bob is attached to a string, it forms a cone and so it is used to illustrate uniform circular motion.

Objective

This experiment enables one to acquire information on uniform circular motion since many have problems relating to it. This helps in sorting out some of these problems.

Materials

• Pendulum
• Motor
• Telescope
• Bob
• String
• Support

Preliminary set up

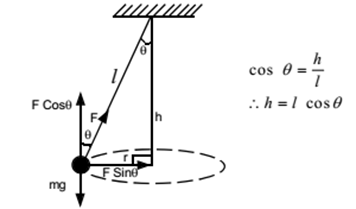
The pendulum used in this case moves in a horizontal circle and so a bob with mass m is connected to a string with length L with its other end attached to firm support. That bob rotates with an angular velocity ω that completes a horizontal orbit with radius r. The vertical distance between the plane of the orbit and the support is assumed to be h with an angle θ between the string and the descending vertical. The string has tension supporting a stationary mass M and a mass m that keeps moving in a loop.

Therefore FT=Mg

Procedure

1. A pendulum with length L was connected to a shaft containing a motor whose rotational speed could be changing by altering the voltage.
2. The speed of the motor and length L was adjusted to allow the period of several revolutions to be measured by observation with values of the angles of rotation.
3. The height h of the pendulum was measured by focusing the telescope on the rotating pendulum while noting down the values on the scale while considering the point of suspension. Whenever the revolution speed increased, it made it difficult for the plane of revolution to keep track of the pendulum path in the telescope.

Data and Calculation

Observation and Analysis

From the results, gravity was fairly constant with few experimental errors and it was close to the standard value of gravitation acceleration which is 980 cm/s2 since the average value from the table is 988 cm/s2(Giacometti, 2020). After computing centripetal force and tension which are physical quantities that relate to circular motion, tension value was bigger than that of centripetal force when the bob was rotating at lower frequencies. When the speed of rotation was increased, both of the values increased similarly. The rotating horizontal plane of the bob was getting lifted in the direction of where it is suspended and the conical path of the string became circular. This shows that tension and centripetal force are similar when it comes to circular motion. Tension is what was causing centripetal force, velocity could increase every time the radius of the circle was increased and decreased when the mass stopped moving.

Conclusion

The conical pendulum well illustrates circular motion and with simple arrangements, gravitational acceleration can be determined. Different ways have to be found to improve the measurements of height h and period in as much as the present measurements are accurate to some extent. Motion can be easier when a string is replaced with a solid rod since a rod has a negative tension and its rigidity helps in supporting the object at its position. Changing different factors in such an experiment affects the results. From this, a relationship of different entities can be verified since I could see velocity change at each trial and so I was able to understand the relationship between variables.

References

Giacometti, J. A. (2020). The motion of a conical pendulum in a rotating frame: The study of the paths, determination of oscillation periods, and the Bravais pendulum. American Journal of Physics, 88(4), 292-297.

Minkin, L., & Sikes, D. (2021). Demonstrating Conical Pendulum Stable and Unstable States. The Physics Teacher, 59(6), 474-476.