Introduction
Research studies that have been carried out do not give conclusive results on the ideal number of stocks required to have a fully diversified portfolio. Some studies indicated that between 30 and 40 stocks while others showed that between 8 and 20 stocks are adequate. Therefore, this paper seeks to carry out a test to verify the optimal number of stocks required to fully achieve the gains of diversification. The study will use the stock of 20 different companies that are listed on the Saudi Stock Exchange (Tadawul). Calculation of the daily returns, average returns, standard deviation, correlations, and covariance will be made to ascertain the minimum number of stocks that are required to attain full diversification.
Portfolio theory and diversification
Before the Markowitz portfolio theory, investors were advised to select stocks that presented the greatest opportunity to gain with a low amount of risk (Markowitz, 1952). This advice was formalized in the portfolio theory after carrying out extensive research and estimations. The portfolio theory provides an approach to analyzing the extent to which a portfolio is good. This is achieved by comparing the variances of different portfolios. A risk-averse investor expects to earn high returns with a low amount of risk. With this, an investor should select a portfolio that gives a combination of the desired standard deviation and expected return in the efficient set. Markowitz emphasized that the selection of a portfolio should be based on the overall risk-reward attributes and not individual risk-reward characteristics (Markowitz, 1952). Thus, out of all possible portfolios, there exist those that create an optimal balance between risk and reward. Such portfolios create the efficient frontier of portfolios. “Markowitz indicated that an investor should select a portfolio that lies on the efficient frontier” (Markowitz, 1952). The Markowitz portfolio theory laid a strong foundation for the modern portfolio theory. For instance, James Tobin added the concept of the risk-free asset to the analysis and this led to the creation of the capital market line and super-efficient portfolio (Tobin, 1958). Further, Sharpe (1964) came up with the capital asset pricing model (Sharpe, 1964). In the model, “the author created a relationship between beta, risk-free assets and expected return” (Sharpe, 1964).
The concept of diversification allows an investor to have several assets in the portfolio. The different classes of assets will enable the investor to maintain the same level of return, as in the case of a single asset, but with a much lower risk. Thus, a combination of risk, return, efficient frontier of portfolios, and diversification assist investors when selecting securities to invest in. The significance of diversification is validated by the modern portfolio theory. However, it is important to establish the number of stocks that will yield adequate diversification. A study carried out by Newbould and Poon (1993) showed that a portfolio that consists of between 8 and 20 stocks was viewed as properly diversified (Newbould & Poon, 1993). However, other research studies indicated that 30 stocks were adequate. Further, studies indicated that the use of more stock in a portfolio led to a reduction of risk. However, not all risks can be eliminated through diversification. For instance, systematic risk is external and cannot be eliminated.
Methodology
The daily stock prices for the twenty companies were collected from the Tadawul website from January 1st, 2014 to January 31st, 2015. Once the prices have been obtained, the daily returns, average returns, standard deviations, correlations, and covariances for the stock were calculated. The correlations and the covariances were estimated by starting with the stock of two companies and adding until all the stocks are exhausted. After carrying out the calculations, a line graph of standard deviation and correlation was drawn.
Findings
The table presented below shows a summary of the calculated standard deviation of the portfolios.
In the graph presented below, the values of standard deviation are plotted against correlation.
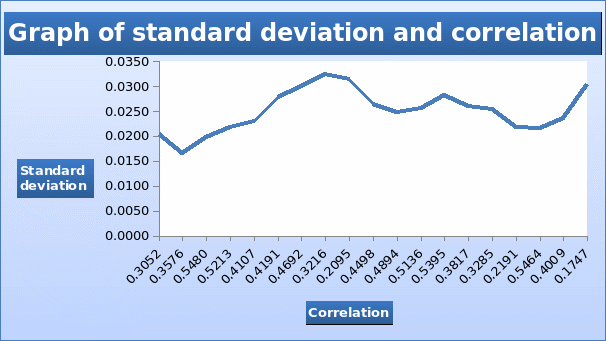
The results show that as more stocks are added to the portfolio, the standard deviation levels off. This can be attributed to the reduced value of the covariance between two stocks. Thus, in the case of Tadawul, 20 stocks are adequate.
Conclusion
The research studies that have been carried out and the analysis carried out in the paper show that the number of stocks required to have a fully diversified portfolio varies across various countries. In the case of Tadawul, 20 stocks are adequate.
References
Markowitz, H. (1952). Portfolio selection. Journal of Finance, 7(1), 77-91
Newbould, G., & Poon, S. (1993). The minimum number of stocks needed for diversification. Financial Practice and Education, 3(3), 85-87.
Sharpe, W. (1964). Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance, 19(3), 425-442.
Tobin, J. (1958). Liquidity preference as behavior towards risk. The Review of Economic Studies, 25(2), 65-86.