Similarities and Differences
Principal components analysis (PCA) and exploratory factor analysis (EFA) have some similarities and differences in the way they reduce variables or dimensionality of a given data sets. One key similarity of PCA and EFA is that both are methods of reducing variables or data based on exhibited variances (Hahs-Vaugh, 2016). The assumptions that underlie PCA and EFA are similar because both require variables to be on ratio or interval scale, exhibit linear relationships, follow the normal distribution, have large sample sizes, and show paired variables with bivariate normal distribution. The steps of their analysis are also similar because they involve selection of variables, extraction of variables, interpretation, rotation, and selection of components or factors that account for most variation (Elliott & Woodward, 2015). However, the main difference between PCA and EFA lies in the way data reduction process occurs. While PCA reduces a set of variables using a linear combination to create principal components with optimal weights that explain most variation, EFA reduces a set of variables using an indirect linear combination of latent variables to develop factors that explain commonality of the variance in data (Hahs-Vaugh, 2016). An additional difference is that whereas PCA decomposes a correlation matrix, EFA decomposes an adjusted correlation matrix with latent factors.
Exploratory Factor Analysis
EFA aids in reducing data by collating variables that have common correlations and grouping them into themes, factors, or components, which effectively account for most commonality in a variable of interest. In exploratory data analysis, EFA uses univariate descriptive statistics, which show patterns and trends of individual variables regarding means, standard deviations, and a valid number of cases assessed. The initial solution offers a percentage of variance explained, eigenvalues, and communalities, whereas KMO and Bartlett’s test of sphericity determines adequacy of a sample used.
As an extraction procedure, EFA uses unweighted least squares (ULS), which gives a common variance that is less than the total variance as in the case of PCA (Meyers, Gamst, & Guarino, 2013). EFA then applies a fixed number of factors in extraction procedure to produce factor correlation matrix and total variance explained by extracted variables. The focus of commonality is significant for the overall analysis for it provides the sum of all correlation values in the component matrix, and thus, it indicates the extent to which the component matrix captures each variable. Meyers, Gamst, and Guarino (2013) explain that the component matrix significantly captures variables with communality values of 0.5 or greater. Hence, communality values help in the extraction of variables that EFA captures in the component matrix as substantial.
Replicated Tables
Principal Component Analysis
Descriptive statistics (Appendix A) display means, standard deviations, and valid cases for each variable. Evidently, the sample size is adequate for each case has 301 valid cases out of 310 cases in the data, which means that only nine cases are missing. Specifically, the mean scores ranged from 2.60 to 8.46 while the standard deviations range from 1.079 to 2.448, which imply that the values of variables are highly diverse.
KMO and Bartlett’s test (Table 1) indicates that the data is sufficient for PCA because it has a coefficient of 0.853 whereas Bartlett’s test of sphericity shows that there is no sufficient correlation (p = 0.000) to hinder PCA.
Table 1.
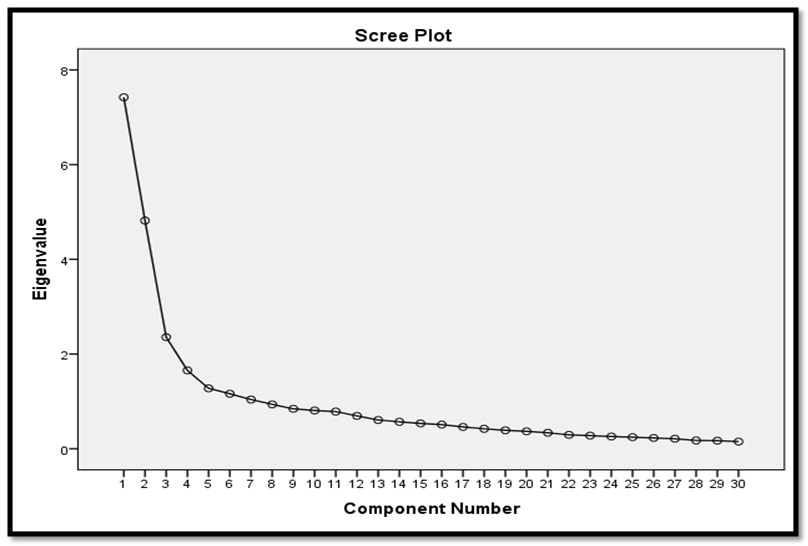
Table 2 below depicts that PCA managed to extract seven principal components with eigenvalues greater than one, and they cumulatively account for 65.8% of the variance. The first and the second principal components have eigenvalues of 7.422 and 4.819, which accounts for about a third of variance (40.8%/65.8%), because each explains 24.8% and 16.1% of variance respectively. The third through the seventh principal components accounts for the remaining a third for each explains 7.9%, 5.5%, 4.3%, 3.9%, and 3.5% of variance respectively.
Table 2.
The scree plot illustrates that the seven components explain most of the variation for the plot begins to regress gradually at the elbow. McCormick, Salcedo, Peck, Wheeler, and Verlen (2017) explain that the elbow of a scree plot sets a threshold of eigenvalues that accounts for most variation. In this view, the scree plot supports the extraction of the seven components in PCA.
Exploratory Factor Analysis: Six-Component Analysis
EFA shows that the unweighted least squares (ULS) procedure explain 53.6% of variance. The first and the second factors account for most variance because they explain 23.4% and 14.5% of variance correspondingly. The third through the sixth factors accounts for minor variance for they explain 6.5%, 4.1%, 3.0%, and 2.1% of variance (Table 3).
Table 3.
Structure Matrix (Appendix B ) shows that the first factor comprises 5, 11, 17, 18, 23, and 29 variables that represent the appealing appearance of the extrinsic orientation whereas the second factor constitutes variables 3, 9, 15, 21, and 27 that represent community feeling aspect of the intrinsic orientation. The third factor representing the affiliation aspect of the intrinsic orientation has 2, 8, 14, 20, and 26 variables while the fourth factor has 4, 10, 16, 22, and 28 variables that represent social recognition aspect of extrinsic orientation. In the fifth factor, 6, 12, 24, and 30 are variables that belong to the financial aspect of the extrinsic orientation whereas the sixth factor has 1, 7, 13, 19, and 25 variables that measure the self-acceptance aspect of the intrinsic orientation.
Evaluation
A strength of PCA and EFA shows that they are effective in reducing variables and grouping them into similar themes that measure a common construct using a linear combination procedure. Another strength is that eigenvalues generated quantifies variance while a scree provides a visual way of selecting components or factors. However, the weaknesses are that PCA and EFA are prone to over-factoring and under-factoring due to the heuristic and arbitrary selection thresholds (Field, 2013). In this view, the analysis using PCA and EFA requires the inclusion of an adequate number of factors or components into the model.
Conclusion
PCA and EFA have significant benefits to projected study for they aid in the development of a Likert scale through the selection of related Likert items, which accounts for most variation in the construct of interest. In this case, PCA and EFA group 30 items into six groups and six groups respectively, which have common themes regarding social orientations of individuals. These groups reveal the existence of subscales in the 30 items used in the study of orientation among individuals.
References
Elliott, A. C., & Woodward, W. A. (2015). IBM SPSS by example: A practical guide to statistical data. Thousand Oaks, CA: SAGE Publications.
Field, A. (2013). Discovering statistics using IBM SPSS statistics (4th ed.). Los Angeles, CA: SAGE Publications.
Hahs-Vaugh, D. (2016). Applied multivariate statistical concepts. London, United Kingdom: Taylor & Francis.
McCormick, K., Salcedo, J., Peck, J., Wheeler, A., & Verlen, J. (2017). SPSS statistics for data analysis and visualization. Indianapolis, IN: Wiley.
Meyers, L. S., Gamst, G., & Guarino, A. J. (2013). Applied multivariate research: Design and interpretation. Los Angeles, LA: SAGE.