Introduction
Quantum tunneling effect is a study that has attracted the attention of many scientists and physicians across the globe. In fact, the application of the quantum effect in daily life events has made various people develop an interest in the study of physics. The Quantum effect has been illustrated using a case where an individual puts a globe in a container. For instance, when a globe has placed a container, in which place should one anticipate getting the globe? Without any doubt, the globe would be found anywhere in the container. However, the Quantum tunneling outcome states that there is hardly any opportunity that the globe could be found somewhere external to the container.
In fact, the Quantum tunneling effect takes place provided a sub-atomic element travels via an obstacle, which ought to be difficult to travel through during any process. In order to discern the assertion correctly, the atoms trying to move through the impending obstructions may be associated with a globe struggling to climb a mountain. Standard physics articulates that when the globe hardly has sufficient dynamism it might be impossible for it to arrive at the next destination. Therefore, the globe lacking adequate dynamism to get through the mountain may be forced to reel backward. Using quantum physics, the sub-atomic elements could pass with minimal likelihood through to the next destination, therefore, passing the obstruction.
Case illustration and derivation
Quantum tunneling appears to be likely to happen due to the tendency appearance of the substance. Perplexing as it appears, within the quantum domain, atoms regularly behave similarly to the marine surfs as opposed to billiard globes. According to Ali and Pham claims, this implies that an electron does not exist in a particular place at a particular time, but rather as a wave of probabilities (p. 23).
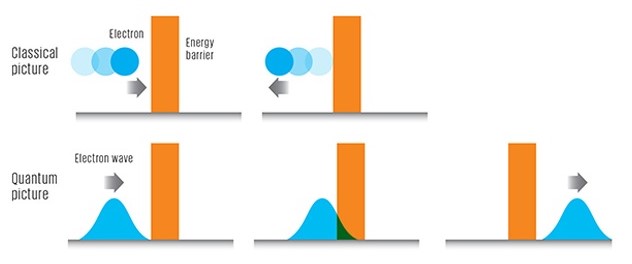
The case illustrates a situation where a particle with energy E is on one side of a one-dimensional potential wall denoted by V. If analyzed using classical physics, if E is less than V, the particle would not pass through the wall. If E is larger than V, then the particle can pass through the wall. Nevertheless, this is not the case for the Quantum system given that the atoms may leak past the blockage even if its energy E is smaller than V. There is a probability that the particle will tunnel through the potential barrier wall and still have the same amount of energy E as before.
Quantum tunneling effects solely relies on probability. However, several variables that affect the probability are the mass of the particle, thickness of the barrier, as well as the difference between the particle’s kinetic energy, and the barrier height (Freiberger 38).
In the “real” world where humans sense by sight and touch, objects physically exist where you can actually sense, see or touch them. In a secretive quantum domain of particularly minute and modest substances (such as electrons), the physical position of these petite matters is “indistinct” and is just a matter of possibility. In quantum physics, it is possible (albeit rarely) to find the particle inside the wall or after the wall in the same location as before as if the wall simply did not exist.
Equation Derivation
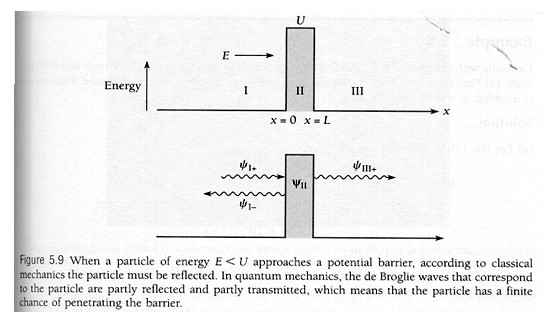
The transmission coefficient abbreviated T is the probability of a particle to tunnel through a barrier or a fraction of the particle wave that makes it move to the other side (Freiberger 36). It is projected through the Schrodinger equations in region I as illustrated below:
Whereby the general equation is
In the above equation, A and B are constants. For we are in the region I where x < -L < 0, thus the exponent of the second term would ever increase for x to -∞. Therefore, to normalize the wave function, constant A should be zero. Then we finally have the equation
For region III, the general equation:
However, in order to keep the wave function normalized we have to set G=0, otherwise the corresponding exponent would ever increase to ∞. Therefore:
Transmission coefficient (t)
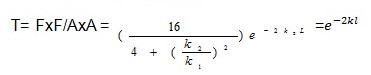
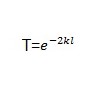
whereby ‘L’ represents the breadth of the obstacle while ‘K’ represents the wavelength integer
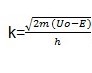
and m is the quantity of the object that we want to tunnel.
The Uo is the potential energy of the barrier wall. In this equation, E is the energy of the tunneling particle (usually kinetic) and h is Plank’s Constant divided by 2*pi (approximately 1.06×10-34 J*s). Therefore, from the equation, since the exponent of the probability function is proportional to the mass and barrier length, we can see that the probability of tunneling decreases exponentially as you increase the mass and barrier length (Cao and Yin 109).
A particle does not have a definite position or momentum prior to measurement. In that case, it seems that a particle prior to measurement is only potentially right here or right there, but it cannot be anywhere and has a definite motion or energy.
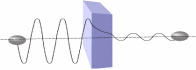
It has been proven that tunneling does not happen in a manner that many people understand. The electron crosses through the barrier by drilling a hole. Nevertheless, the truth is that they merely emerge on the opposite area. Subsequent to channeling the surf, the force becomes frailer and the surf-span appears to be similar to the initial tendency.
Whereas the likelihood of channeling could be disregarded at macroscopic intensities of the “material domain”, it happens often on the Nano gage phases. For example, during radioactive decay, the alpha particles try to escape from the unstable nuclei (Auletta and Fortunato 152). The atoms appear to be seized in the nuclei by the atomic bonds, which according to standards ought not to be capable of escaping. Nevertheless, the alpha particles do escape using the phenomena of Quantum tunneling occurring via the use of wave-like property of the particles.
The same happens in the sun given that the production of light is essential to our universe. Two-light atomic light nuclei fuse from collision to form a new element and in the process, light is produced. Nevertheless, given that both these nuclei are positively charged, they tend to repel one another (Griffiths 67). In classical physics reasoning, they can only break their potential barriers and fuse (collide) if they have enough energy to overcome that potential barrier named U. Unfortunately, the nuclei in the sun do not have enough energy to break the barrier, but the sun still shines and that happens based on Quantum tunneling.
Conclusion
In conclusion, Quantum tunneling effect draws sub-atomic particles crosswise over boundaries, but they cannot cross naturally. The sum of particles that moves across the barrier lowers exponentially with the increment in the barrier width. In addition, the number of particles that moves across the barrier rises with the kinetic energy of the particle. One astonishing yet genuine aspect of quantum tunneling is that the sub-nuclear particles that cross the barrier do so literally instantaneously (Beth and Leuchs 163). The particles hardly need time in order to pass through the obstacle since they merely bounce above the available area within a twinkle of an eye. The occurrence appears to be an additional, but strange fact about quantum process. Particles can intently go from one spot to another without passing through the space in the middle.
References
Ali, Mohammad and Pham, Yvonne. Quantum Tunneling: SRJC PHYS43. New York, NY: Sage, 2014. Print.
Auletta, Gennaro and Mauro Fortunato. Quantum Mechanics. London, UK: Cambridge University Press, 2009. Print.
Beth, Thomas and Gerd Leuchs. Quantum Information Processing. Hoboken, New Jersey: John Wiley & Sons, 2006. Print.
Cao, Zhuangqi and Cheng Yin. Advances in One-Dimensional Wave Mechanics: Towards A Unified Classical View. Springer Science & Business Media, 2014. Print.
Freiberger, Marianne. Schrödinger’s Equation: In Action. University of Cambridge: Foundations of Quantum Physics, 2012. Print.


