Introduction
Projectile motion is an example of motion in two dimensions with a constant velocity of the object in one dimension and constant acceleration in the transverse direction. A very common example of such a motion is that of the cannonballs fired from a canon. Cannonballs can be fired from cannon at different velocities and different angles θ with respect to the ground. The horizontal velocity of the cannonballs then remains vCosθ throughout the motion, while its vertical velocity remains vSinθ – gt; where g is the acceleration due to gravity and remains constant throughout the motion. At any point in time t, the horizontal displacement is given by
x = vCosθ *t; and vertical displacement is given by y = vSinθ *t – (1/2)*g*t2.
Eliminating t from the expressions of x and y gives a relationship between y and x or the equation of path and this equation is a parabolic equation. Thus the path of a projectile is a parabola. To investigate the motion of a projectile the following experiment can be designed.
Experiment Design
To investigate projectile motion one would need a steel ball of say 100 g mass, a hammer to hit the ball, a platform with provision to change its height (h) and slope (θ), a stopwatch to measure the time of flight (t) and a measuring tape to measure range (R) of the projectile. The ball will be hit from different heights and inclinations (of the platform) and the range of the projectile (R) and time of flight will be measured. The measured values will then be used to calculate the initial velocity of the ball and the height of the platform. The calculated value for the height of the platform and the set value of the same must confirm to prove the hypothesis of projectile motion. Any error shall be attributed to an error in measurement of the range of the projectile, time of flight, and the fact that the air resistance was neglected in these calculations.
Objective
A virtual experiment was carried out to understand some of the aspects of the projectile motion. In these experiments for the sake of simplicity, the angle of inclination was kept zero, and the height of the projectile was varied. This was done to understand the effect of the height on projectile motion. In another set of the experiment, the height was kept constant and velocity was varied to understand the effect of initial velocity on the projectile motion.
The data from these experiments are presented below in Tables 1 and 2.
Data and Results
Table 1: Effect of height on the projectile motion.
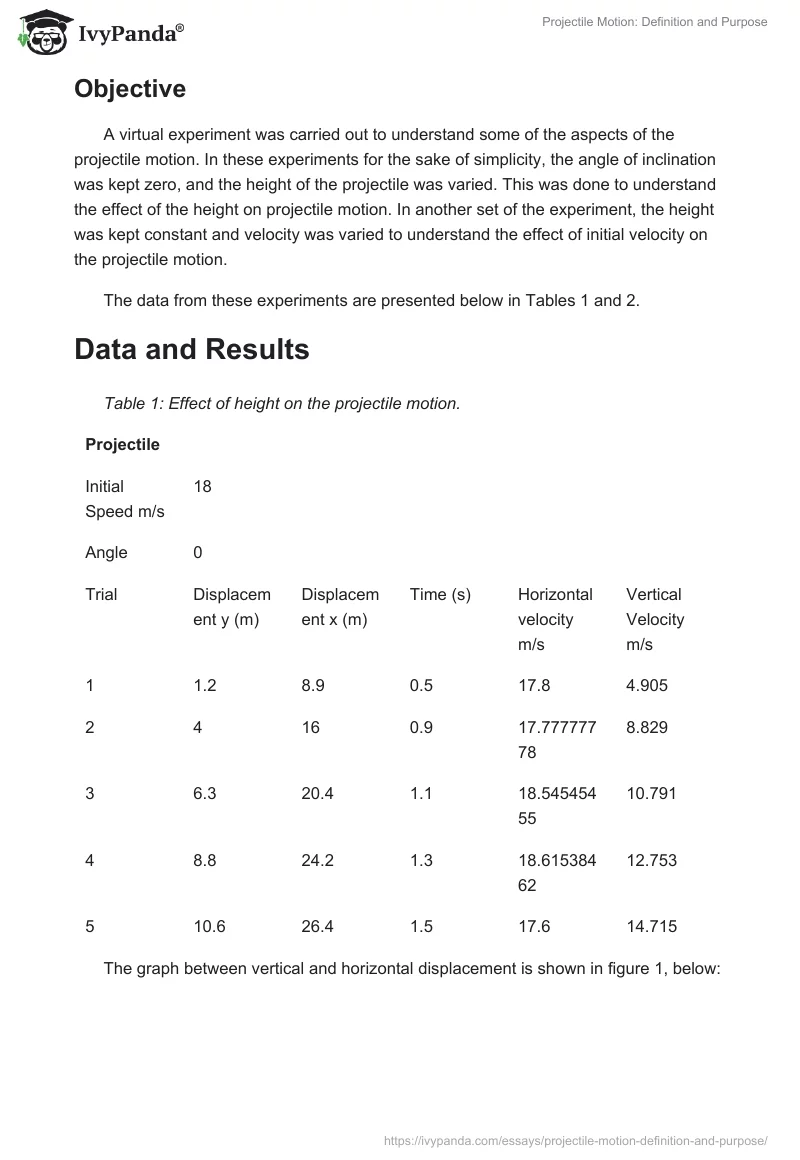
The graph between vertical and horizontal displacement is shown in figure 1, below:
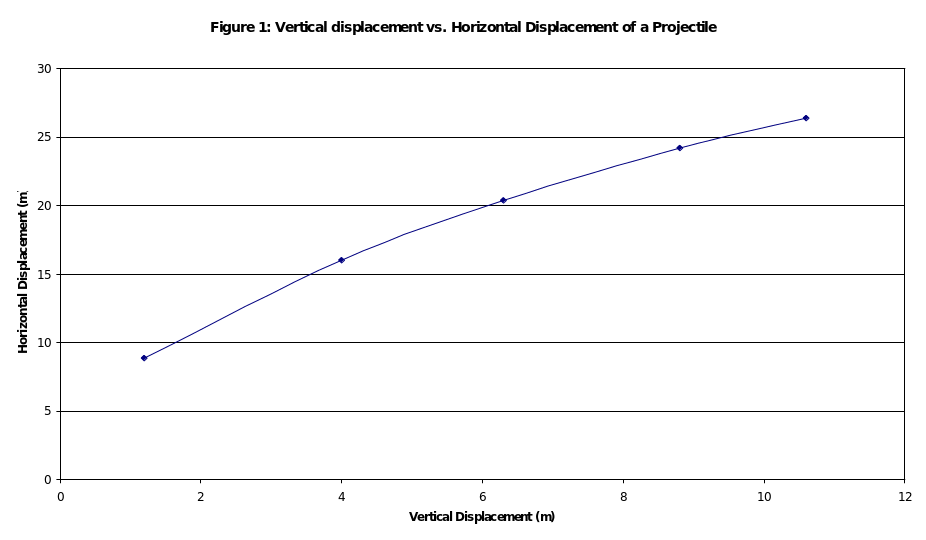
The graph between vertical displacement and time is shown in figure 2, below:
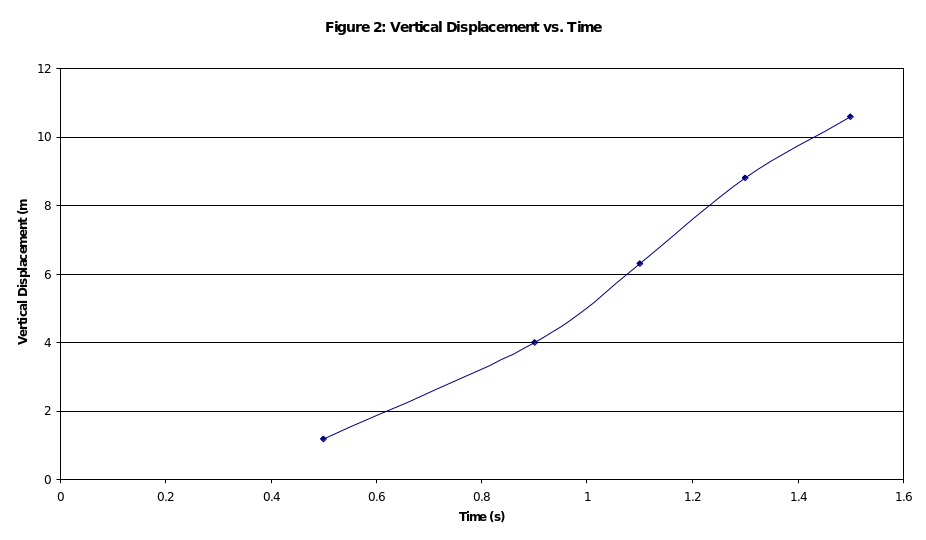
Table 2 below presents the effect of initial velocity on projectile motion.
The graph between time and initial speed is shown in figure 3, below:
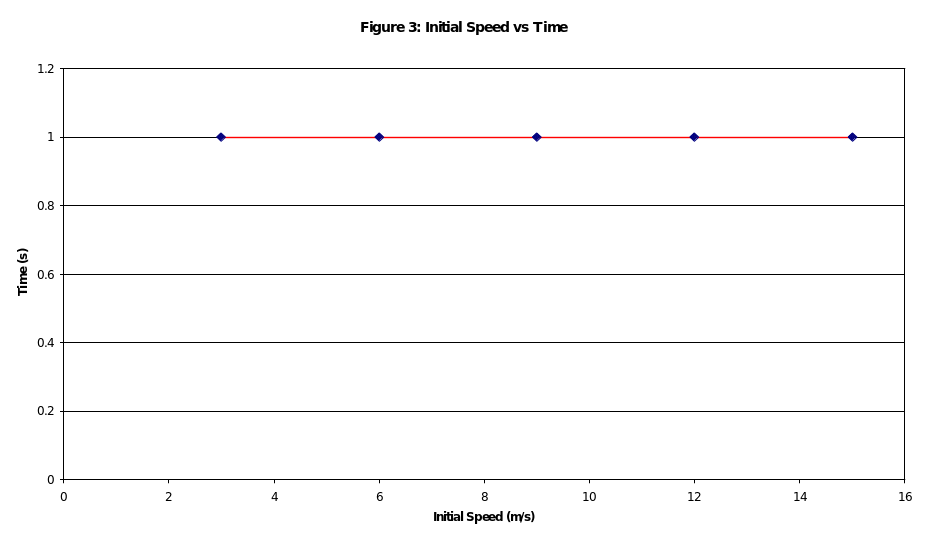
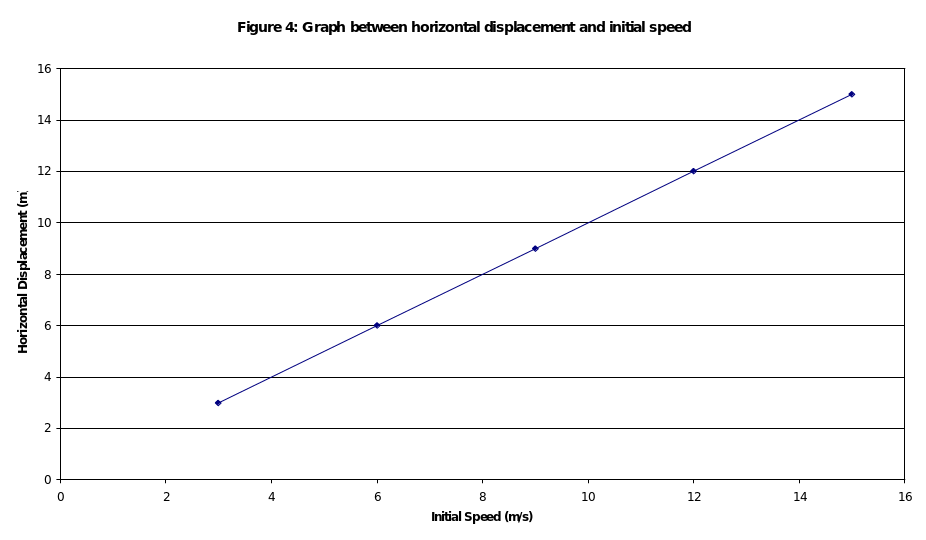
The graph between time and initial speed is shown in figure 4, below:
Conclusions
Time of motion increases with increasing vertical displacement as acceleration in the vertically downward direction is constant. This is a parabolic relationship as a time of flight is related to vertical displacement by y = (1/2)gt2; this relationship is also clearly visible in figure 2.
As horizontal velocity remains constant throughout the motion; therefore, increasing vertical displacement, which increases the time of flight leads to an increase in horizontal displacement as well. This relationship is also parabolic in nature as depicted in figure 1.
Increasing initial velocity leads to increasing horizontal displacement and this relationship is linear (figure 4).
Time of motion is not at all related to the initial velocity (figure 3). This is because the angle of the projectile is 0 deg. Had this angle been non-zero there would have been non-zero vertical velocity and this would have then impacted the time of flight.
Calculations in table 1 and table 2 show a very good match between the initial velocity and the calculated horizontal velocity. There is a small mismatch between the set value and the calculated value. Despite the experiment having been done in a virtual setting the small mismatch is due to the truncation error of time measurement. It should be noted that the time measurement is limited to a certain number of decimal places and this requires truncation and leads to truncation error and the observed mismatch between the initial velocity and the calculated horizontal velocity in table 1.
The projectile thrown from the greatest height will have the greatest total velocity as the vertical velocity increases with increasing height and horizontal velocity remains constant; therefore the total velocity which is the vector sum of the horizontal and vertical velocity will also be greatest with the greatest height.