Introduction
Steel is a valuable metal in civil engineering processes. The application of steel in these applications is attributed to its physical, chemical, electrical and mechanical properties (El-Reedy, 2017). Some of the mechanical properties of steel that determine its specific uses are hardness, tensile strength, elasticity, weldability and machinability (Bhaduri, 2018).
The mechanical properties of steel are determined by the chemical composition and manufacturing procedures. Therefore, steel may be processed differently to suit the requirements of various civil engineering applications that involve welding, drilling, forging, heat treatment and machining.
The expected Young’s modulus of steel should range between 190 and 210 GPa (Rao, 2017). Conversely, the maximum allowable value of yield strength is 650 MPa. Yield strength can be described as the tensile stress value where at least 95% of steel samples have a 90% likelihood of high yield strength.
Experimental Method
A piece of steel bar was provided for tensile testing. The sample was mounted in the grips of a Zwick Roell z250 testing machine that was controlled by the testExpert II software. An extensometer was mounted on the specimen to monitor the extension of the specimen. The test was continued until the specimen fractured. Load, extension and crosshead deflection were recorded by the software during the test and were converted by the software into stress and strain values. The outputs were used to compute parameters such as yield strength, ultimate tensile strength, 0.1% proof stress and Young’s modulus.
Results
Figure 1 shows the stress-strain curve that was obtained from the experiment. The yield strength was visualised on the curve as maximum stress just before a slight reduction. Its value was 540 MPa. The maximum strength recorded represented the ultimate tensile strength and was 622 MPa. The stress at the end of the experiment gave the breaking strength and was 504.56 MPa.
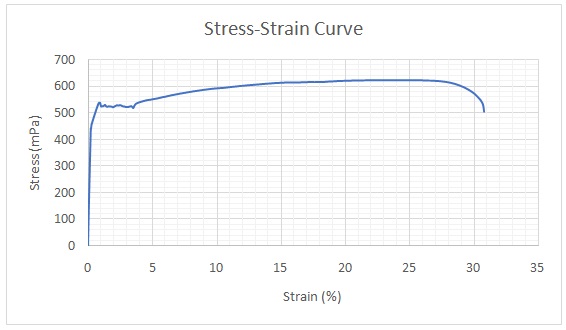
The stress-strain curve was re-plotted in the range of 0 to 1% strain to calculate Young’s modulus and 0.1% proof of stress, which is represented in Figure 2.
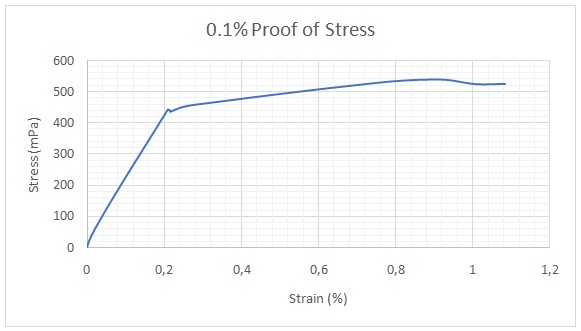
From figure 3, it is evident that the stress-strain relationship was linear to a strain of approximately 0.21%. Therefore, any two points between zero and this point could be used to compute Young’s modulus using the following equation:
Young’s modulus= Gradient of the straight-line section of the stress-strain curve
= y2-y1/x2-x1 where (x1, y1) and (x2, y2) are coordinates of two points on the straight line.
= (188.313- 18.3887)/ (0.0814096- 0.0042)
= 169.9243/ 0.0772096
= 2,201.04 MPa
= 2.201 GPa
The proof of stress was found by determining the point of intersection of the breaking strength point with the curve, which was approximately 435 MPa. A summary of the overall outcomes is provided in Table 1.
Table 1: Tensile stress outcomes.
Discussion
The observed value of Young’s modulus was 2.201 GPa, which was lower than the expected range of 190 and 215 GPa. This observation means that it had low elasticity and susceptible to distortion at low forces (Chen, Gandhi, Lee, & Wagoner, 2016). The observed yield strength was 540 MPa, which was within the expected limits given that the maximum allowable value is 650 MPa (Hajibagheri, Heidari, & Amini, 2019).
The experiment tested only one steel sample. Hence, the outcomes are not representative of the consistency of the entire batch from which the sample originated. There is a need to analyse more than one sample, conduct statistical evaluations of the outcomes before concluding whether or not the tensile properties are within the expected range.
Conclusion
Only one steel specimen was tested. The observed Young’s modulus was lower than expected. However, other tensile strength parameters matched the requirements of reinforcing steel. Additional testing should be done using more samples to ascertain the tensile properties.
References
Bhaduri, A. (2018). Mechanical properties and working of metals and alloys. Gateway East, Singapore: Springer Nature Singapore.
Chen, Z., Gandhi, U., Lee, J., & Wagoner, R. H. (2016). Variation and consistency of Young’s modulus in steel. Journal of Materials Processing Technology, 227, 227-243.
El-Reedy, M. A. (2017). Steel-reinforced concrete structures: Assessment and repair of corrosion. Boca Raton, FL: CRC Press.
Hajibagheri, H. R., Heidari, A., & Amini, R. (2019). Experimental relationship of yield and tensile strengths with hardness in high strength APIX70 steel pipes. Modares Mechanical Engineering, 19(1), 85-93.
Rao, P. D. (2017). Strength of materials: A practical approach (Vol. 1). Hyderabad, India: Universities Press.