Abstract
The capacity of stainless steel to withstand fire conditions can be determined from the stress-strain relationships. This report analyses the mechanical properties of EN 1.4301 and EN 1.4462 stainless steel types in order to explain how these properties affect the stress-strain relationships. It also reviews past studies into the material properties of steel under fire conditions and examines the various models proposed for steel fire designs. The analysis bases on two tests, the steady state and transient-state tests, which can explain the behavior of steel at elevated temperatures. Stress-strain relationships provide an accurate prediction of the properties of stainless steel under fire conditions. Engineers and studies have conducted many studies involving both transient-state and steady state tests to determine the material properties of steel under fire conditions.
This work explores the mechanical attributes data of stainless steel at sublime temperatures. Accurate predictions of the material properties including yield strength, elastic modulus and ultimate strength at elevated temperatures, of between 20◦C to 900◦C, proposed by different studies compare with the European, American, and British standards. Furthermore, other studies propose a strain-stress model of stainless steel at elevated temperatures. The stress-strain relationship is important in evaluating the capacity of stainless steel to withstand fire conditions.
Introduction
In fire design models of various materials, factors such as yield strength of the material, the shape and dimensions of cross-section and reduction factors for yield strength and elastic modulus provide relevant data for designing fire resistant material. Buchanen, Moss, Seputro, and Welsh (2004) posit that, the stress-strain relationship of a material “at elevated temperatures is important in assessing the load-bearing level of the structure when in fire condition” (p.1505). For a steel structure to exhibit mechanical resistance to fire, its load-bearing function should be high in exposure to relevant fire conditions. In addition, in order to study the deformation processes during high rate strain deformation, the analyst should apply deformation modes of the load bearing structure, micro-twins, and micro-bands, for both carbon and stainless steels.
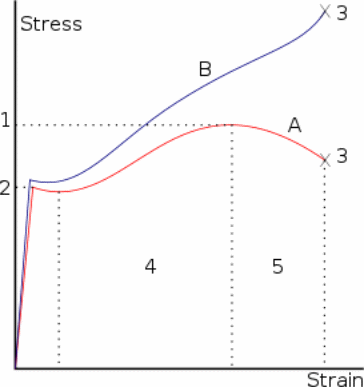
In most structural applications, Engineers use austenitic and duplex steels. Austenitic steels have a combination of good qualities including a high design strength of 220N/mm2, corrosion resistance and fabrication properties. The commonly used austenitic stainless steel grades include 304/304L and 316/316L while the most commonly used duplex stainless steel is grade 1.4462. Steady-state tensile tests and transient states determine the stress-strain relationships at high temperature conditions for stainless steel (Drysdale 1999, p. 87).The stress-strain relationship for carbon steel is different from that of stainless steel (figures 1 and 2).
From a stress-strain curve, structural engineers determine the mechanical properties of stainless steel such as elastic modulus, yield strength, ultimate strength, and strain. The non-linear stress-strain relationship of stainless steel is an indication that its behavior is sensitive to elevated temperature and yield stress. As a result, to establish a non-numerical model for steel structures, the stress-strain relationship is important. The stress-strain relationship and the mechanical properties of stainless steel at elevated temperatures are important in fire design models for steel.
Literature Review
The Steady-State test
To study the behavior of stainless steel at elevated temperatures, the material data of the steel obtained through testing is important. ca Steady-state tensile tests and transient-state procedures determine the stress-strain relationships of stainless steel at high temperature conditions. Steady-state tests are of two types; strain controlled tests, whereby strain is maintained as a constant while the load is varied or load-controlled tests, where the load rate is maintained at a constant level. To generate data for fire design guidance of stainless steel, the steady state tests are therefore important. Outinen, Kaitila, and Makelainen (2000) conducted isothermal material tests (steady-state tests) for cold worked materials at elevated temperature (p. 6). They used three types of austenitic stainless steel: the Polarit 761, Polarit, 731 and Polarit, 711 in these tests. In steady-state tests, they heated the test material to a specified temperature before applying the tensile load. In their experiment, they maintained constant temperature as they varied the loads. The temperature in steady-state tests is maintained at a specified level while the load is continually changed. This means that only the load rate has an effect on the results, as the temperature is a constant. The stress at a particular strain normally decreases with the load rate (Sakumoto, Nakazato, & Matsuzaki 1996, p.399).
In contrast to carbon steels, stainless steel stress-strain relationship is non-linear with no clear yield point (Figures 1 and 2). As a result, engineers define the yield stress/strain (point) for stainless steel in reference to a 0.2% proof strain (Eurocode 2001, p. 3). Outinen, Kaitila and Makelainen obtained stress values in relation to different proof strains including 0.1%, 0.2% and 2%, measured the values of modulus of elasticity and tensile strength of the material before comparing these values with pr EN 1993-1-2 [1] values (2000, p. 11). The three test materials behaved differently with regard to stress-strain relationships. Outinen and Makelainen carried out steady state tests on stainless steel grade EN 1.4301 using a tensile testing machine (2001, p. 3). The stress-strain values for cold formed material compared to those of the base material. In both tests, they obtained the modulus of elasticity values, which is the stress-strain ratio at a single point, from the stress-strain curves and compared with standard values.
The Transient State Tests
Transient state tests involve subjecting the test material to constant tensile stress and increasing temperature. The gradual increase in temperature is due to two reasons; firstly, in load-controlled tests, there is a rapid loss of tensile strength, which the loading machine cannot measure when the temperature rapidly increases. Secondly, for each specified temperature, the analyst needs the strain data for the conversion of the transient test results into stress-strain curves (Rhodes 1991, p. 231). This test involves temperature and strain measurement to generate temperature-strain curves. Such curves provide important strain properties of the material at elevated temperatures. The analyst deducts thermal elongation, the expansion due to heating, from the total strain. The analyst then converts the resultant results to stress-strain curves before establishing the mechanical attributes of the stainless steel. The transient-state method, in comparison to the steady-state method, gives a more realistic technique for determining the behavior of stainless steel under fire situations.
Chen and Young, in carrying out transient tests for stainless steel, placed the specimen under a constant tensile stress levels while increasing the temperature systematically from 100 0C to 9000C at equal intervals of 100oC (2005, p. 229). They used these transient test results to construct stress-strain curves, which give the elastic modulus values at different temperatures for any given specimen. To determine the expansion level of the specimen after exposure to conditions of fire, Chen and Young measured the thermal elongation of the material at 2MPa tensile stress level and then compared these values with the BS 5950-8 and EC3-1.2 thermal elongation values for EN 1.4462 stainless steel. In comparison to European Code 3 and the British Standard 5950-8, their thermal elongation values were lower than the predicted values. They used the reduction factors, which represent the ratio involving the yield strengths of the stainless steel to normal room temperature of 22 0 C for stainless steel types EN 1.4301 and EN 1.4462 at proof strains of 0.2%, 0.5%, 1.5 % and 2 %. Plotting the reduction factors against different temperatures indicated that, for the two types of stainless steel tested by Chen and Young, the steady state values were equivalent to transient state values at 0.2% yield strengths (2005, p. 232).
Outinen and Makelainen conducted the transient tests for stainless steel EN 1.4301 different stress levels with the temperature rate maintained at 200C, 100C and 300C (2001, p. 2). In addition, they subjected some test material, base material and cold-formed material to high temperature rates in order to determine the behavior of the material at high temperatures. The cold-formed material had higher yield strength in this experiment (almost twice) compared to the base material. The mechanical properties other than “yield strength such as modulus of elasticity, yield stress, and thermal elongation were also higher in cold-formed material compared to the base material” (Outinen & Makelainen 2001, p.4). Again, the stress-strain curves for transient state tests and steady-state tests were almost similar in this experiment, showing a clear uniformity of the results obtained from different tests.
At elevated temperatures, the stress-strain curve of the stainless steel is important in the design of stainless steel for fire. Most of the stress-strain models bases on hot rolled stainless steel. Chen and Young proposed a stress-strain curve model for cold formed stainless steel at elevated temperatures (2005, p. 235). The model bases on steady-state results for EN 1.4462 and EN 1.4301 types of stainless steel.
The Mechanical Properties of Stainless Steel at Elevated Temperatures
Different stainless steel types exhibit different mechanical properties at elevated temperatures. To understand the behavior and the stress-strain relationship of stainless steel in fire conditions, the mechanical properties such as elastic modulus, yield strength and proportional limit are important (Rasmussen 2003, p. 47). The European standard for the structural design of steel structures provides a reference for examining these properties. The stress-strain curves converted from both steady and transient test results present these stainless steels’ mechanical properties: elastic modulus, ultimate stress, and yield strength (Ramberg, & Osgood 1973, p. 47).
Elastic Modulus
The modulus of elasticity (E) is the modulus tangent at a point in the linear curve relative to the initial section of the curve, where the curve is linear. For steel, “the elastic modulus is a constant over a range of strains” (Myllymaki 2001, p. 8). In Chen and Young tests, they first converted the transient-test results into stress-strain curves from which they obtained the elastic modulus. The data obtained for each stainless steel specimen is normalized by comparing it with the initial elastic modulus in order to eliminate the minor variations in elastic modulus (2005, p. 236). Chen and Young’s repeated the transient tests to minimize the variations in the elastic modulus.
In determining the modulus of elasticity of EN 1.4301 stainless steel, Outinen and Makelainen used both the transient state and the steady state results and compared each specimen to the values obtained at the initial part of the stress-strain curves (2001, p. 5). The results from the different tests varied greatly hence the need to compare the results from various tests. After comparing the different tests, Outlinen and Makelainen found that the modulus of elasticity for stainless steel EN 1.4301 dropped with increase in temperature (2001, p. 5).
To determine the reduction factor for elastic modulus, Outinen and Makelein in their tests, used the transient-test results obtained from base material and strain-hardened material to construct stress-strain curves. It is also possible to determine the reduction factors for elastic modulus from steady-state tensile tests (Ala-Outinen, & Oksanen 1997, p. 21). Since the proportional limit of austenitic stainless is not clear, it is difficult to determine the reduction factor and the elastic modulus from their stress-strain curves. Therefore, a linear regression analysis of the transient-test results enhances the determination of the reduction factor for the elastic modulus. Outinen, Kaitila and Makelainen carried out an extensive experiment aimed at determining the mechanical properties of structural steels S355 and S460 with yield strength (fy) =355 N/mm2 and fy =460N/mm2 respectively (2000, p. 13)
The Yield Strength
To determine the yield strength of stainless steel, analysts usually use the 0.2% non-proportional strain. The yield strength refers to the level of stress that can cause permanent deformation. It is the point beyond which permanent deformation occurs. It is normally determined from the early portions of stress-strain curves. In Eurocode 3, the yield strength bases on 2% strain (EC3, 2007, p.2). Outinen and Makelainen determined the yield strength from stress-strain curves derived from the transient-test results (2001, p. 7). They compared the base material of EN 1.4301 and cold formed material of the same stainless steel at 0.2% strain. The yield strength of EN 1.4301 base material was lower than that of the cold-formed material at moderate temperature (22oC). Using stainless steel types EN 1.4301 and EN 1.4462, Chen and Young on the other hand, involved four strain levels; the 0.2%, 0.5%, 1.55, and 2.0% at different temperatures. They obtained reduction factors for yield strength in the tests, which was expressed as a ratio between various yield strengths relative to room temperature.
The Australian Standard (AS 4100) provides the standard for predicting the yield strength for steel types EN 1.4301 and EN 1.4571 within 400oC and 900oC range of temperatures. On comparing the yield strengths obtained, Chen and Young found out that the ASI 4100(4) prediction was only conservative between 600oC and 900oC and did not predict well the yield strength for temperatures below 400oC. However, the yield strengths results obtained by Chen and Young were close to Ala-Outinen and Oksanen results for both transient and steady test results.
Therefore, they found AS 4100 prediction inapplicable for temperatures less than 400oC. Chen and Young proposed a new equation for predicting the yield strength for cold-formed stainless steel at elevated temperatures. Using the new equation, the values of the reduction factor for yield strength correspond to the stainless steel test results. The reduction factors of 0.5%, 1.5%, and 2%, for both hot-formed and cold-formed stainless steel types EN 1.4462 and EN 1.4301, the yield strength predicted by the British standard applies within the temperature range of 550oC to 960oC. In other words, the reduction factor for yield strength of cold-formed stainless steel is much higher than the values provided in the ASI 4100. Chen and Young found that the yield strength values for cold-formed material were higher, on average, to the nominal values provided in the Eurocode 3 at a temperature beyond 600oC.
One of the most important factors in modeling of stainless steel mechanical properties at elevated temperatures is the yield strength. According to Eurocode 3, the achievement of yield limit for hot rolled steels is possible at 2% total strain at room temperature conditions (EC3, 2001, p. 2). However, Ala-Outinen proposed the use of 0.2% proof stress for those structural members (columns) affected by buckling modes and 1.5% proof stress for those may fail due to bending (beams) (1996, p. 12).
Ultimate Strength/strain
Ultimate strength is the maximum stress that the stainless steel can withstand (Cheaitani, & Burdekin 1993, p. 21). Chen and Young using the steady-state results for the ultimate strength for stainless steel type EN 1.44262 and type EN 1.4301, found out that the reduction values for type EN 1.44462 were higher than that of EN 1.4301 for all test temperatures. Chen and Young propose an equation that can predict the ultimate strength of stainless steel. The unified equation predictions correspond with the test values obtained for stainless steel type 1.4462 and EN 1.4301. The ultimate strength of stainless steel measures the maximum capacity of temperature that the steel structure can bear, beyond which it can withstand no additional temperature.
Caldwell (1965) attempted to evaluate the ultimate strength of a steel ship structure by using a rigid plastic mechanism analysis (p. 411). To evaluate the ultimate strength of stainless steel and structural members, structural analysis is important. When performing the structural analysis, the engineer must consider the buckling effect and yielding of the steel. Experts refer this technique to as electro-plastic large deflection analysis.
Fire Resistance Design
Fire design for stainless steel forms an essential component of the design procedure of steel structural members. The methods used for fire design of stainless steel ensure that the structure designed to operate in the normal room temperature (22oC) can further withstand the additional increase in temperature. The engineer subjects the material to fire, for a certain duration set for a specific structural steel component. There are three ways to perform an effective design for fire: computationally, use of tabulated data or by use of both methods. The steel design should incorporate fire protection materials to protect the structures from fire and enhance their stability in case of fire. The fire resistance time is a common criterion used to test for fire resistance of a steel structure. The fire resistance time refers to the time from the start of a fire to the time when the load bearing capacity of the steel decreases to the level of the loads (Iso-Mustajärvi, & Inha 1999, p. 59). The fire design criterion is important in determining the resistance of the steel structure with regard to the highest temperature attained and the loads the fire subjects to the structure. Steel structures fall into four different groups based on the required fire resistance time: the R15-, R30-, R60- and R90-classes, with R15 representing the ‘resistance’ of the material followed by the fire resistance time in minutes.
The Eurocode 3 part 1.2 provides simple calculation models for fire design of stainless steel structures. The calculation applies c to Class 1 and 2 cross-sections.
However, under certain restrictions the rules can also apply to Class 3 and 4 cross-sections. The buckling effect is more significant in thin-walled cross-sections, particularly in class 4 cross-sections (Hautala, & Schmidt 1998, p. 71). Since the fire design methods are limited, standards recommend that the engineers should not subject the cold-formed stainless steel to a temperature exceeding 350oC at any given time, otherwise, they should use a thick layer of an insulator with steel, which is often uneconomical and a difficult fire design. Eurocode 3 specifications allow a partial safety factor of 1.0 for all load combinations in fire conditions (EC3, 2001, p.3).
Among the important studies carried out to determine the behavior of cold formed stainless steel under fire conditions was that by Ala-Outinen. The study involved experimental and numerical analysis of buckling effect of rectangular hollow sections (RHS). Engineers commonly use the RHS materials as building and roofing materials. In his study, Ala-Outinen subjected columns of RHS, 90mmm long, to transient state tests at an elevated temperature of 300oC for duration of three minutes (Ala-Outinen 1996, p.16). Subsequently, he increased the temperature at the rate of 10oC per minute. The study found out that local buckling led to the columns losing their load bearing capacity at mid-length for concentrically loaded columns and near the top of the column for eccentrically loaded columns.
Based on the equations of the Eurocode 3 part 1.3, Ala-Outinen proposed a calculation method for a room temperature design. To determine the width of the columns, he recommended that the values of the modulus of elasticity and yield strength be reduced in line with the Eurocode 3, part 1.2 (1996, p. 21). In this particular study, the set stress values were equal to the yield strength at 0.2% strain. The Eurocode 1, part 2.2 provides guidelines for determining the load reduction factor, which usually lies in the range of 0.6-0.7. The load reduction factor helps to construct a load bearing capacity curve. The curve provides for calculation of the critical temperature of the material. Ala-Outinen found that the critical temperature for the columns tested at load reduction factor, 0.7, to be around 400oC using this procedure (Ala-Outinen 1996, p. 24). The critical temperature, thus obtained, is significantly higher than the 350oC contained in the Eurocode 3, part 1.2.
Structural Fire Design Models for Stainless Steel
There exist many models for predicting the failure temperature of steel wall studs. Gernlich proposed a method for determination of the level of resistance of steel wall studs (Ranby 1999, p. 31). This model employs equations for reduction of the modulus of elasticity and the yield strength as recommended in the AISI standard. The method involves first determining the stresses at the cross-section due to eternal loads before the calculation of the critical temperature. The critical temperature in this case is the temperature at which yield strength of steel is equivalent to the stress applied (Guedes, Gordo, & Teixeira 1998, p.179). The next step involves calculation time of failure as a function of temperature rise. This model considers the deflection that arises due to bending. However, the model neglects the buckling effects.
Alfawakhiri and Sultan (2000) model involved use of load bearing lightweight steel framed (LSF) walls exposed to fire on a single side (p. 73). The authors tested six different configurations of the LSF walls each containing cold-formed steel wall studs sandwiched with two layers fire-resistant gypsum board each12.7 mm thick. Materials used as insulators included wool, glass, and cellulose. They suggested a fire resistance model for load-bearing LSF walls based on steady state and transient-state tests. The major limitation of this model is its assumption that fire prevents buckling.
Another fire design model is the one proposed by Feng, Wang and Davies (2001, p. 65). The authors conducted preliminary tests and compared their results to the European, British and American design models. They subjected the test material to steady-state tests, where they first exposed the test material to elevated temperature before subjecting it to a load. Using reduced modulus of elasticity values at 0.2% proof stress- as suggested in the Eurocode 3 part 1.2, engineers can make analytical predictions. The authors concluded that the critical temperature of thin-walled steel walls at load ratio of 0.7 is significantly higher than the 350oC as suggested by Eurocode 3. In addition, the study concluded that the reduced material properties extend the temperature beyond the 350oC. However, the study failed to include the temperature gradients and buckling modes in the analytical predictions.
In contrast to Feng et al. study, Lee, Mahendran, and Makelainen (2001, p. 17) involved the buckling behavior of thin walled test material. Lee et al. used 400mm sections of test material just as Feng et al study revealed. Lee et al then subjected these materials to steady state tests. Lee at al. then used the test results obtained and finite element analysis results to calculate the buckling coefficient, kT, at elevated temperatures. This study found out that finite element analysis could model the behavior of steel in fire conditions. However, the use of small lengths of the test specimens limited the buckling modes in this study.
During a fire situation, the inner and the exposed sides of the steel wall studs normally experience different temperatures causing a steep temperature gradient within the cold-formed steel studs. Typically, the exposed side can have an average of 300°C higher than the external side (Young, & Rasmussen 1998, p. 140). This means that the mechanical properties of steel subjected to fire are highly affected at the side exposed to fire compared to the external side. At the same time, thermal elongation is much higher on the fireside than on the external side, which makes the steel studs to deflect towards the fire source (Buchanan and Klippstein 1978, p. 89). As a result, the axial compression forces acting on the steel studs produce bending that leads to flexural buckling directed towards the fire. In practice, therefore, the flexural buckling is the relevant buckling mode. However, the use of insulation material such as gypsum board prevents flexural, torsional, and flexural-torsional buckling (Chen, & Young 2004, p139).
Flexural-Torsional Buckling
Eurocode 3 provides equations for evaluating the ultimate strength, the flexural, and the torsion-flexural buckling strength. When stainless steel undergoes compression, it experiences lateral bending and deflection occurs (Uy, & Bradford 1995, p. 53). The material then buckles. When the axial load increases, lateral deflections also increase causing the material to collapse. Steel under compression may buckle in three different ways: torsional buckling, flexural buckling, or a combination of both flexural and torsional buckling (Nylander 1956, p. 7).
Flexural buckling occurs when the material buckles in a cross-section by bending in the plane of symmetry whereas torsional-flexural buckling occurs in cruciform sections whereby torsional buckling (twisting) occurs before flexural buckling (bending) at symmetrical or unsymmetrical cross sections. Ranby (1999, p. 34) presents a method of evaluating the yield and the buckling strengths. Both torsion and flexure can occur at a single symmetric section leading to buckling at the line of symmetry. For steel, “the flexural buckling is more in symmetrical sections than in non-symmetrical sections…Torsion-buckling mode is common in non-symmetrical sections regardless of the dimensions or shape of the section” (Thonton 1993, p.485). However, steel beams exhibit torsion resistance to compression at elevated temperatures.
Uy and Bradford (1994, p. 259) used a geometrically non-linear finite element analysis to evaluate the torsion resistance of steel beams at elevated temperatures based on the mechanical properties of steel provided in Eurocode 3, part 1.2 (EC3 2001, p. 3). In their study, the fact that stress-strain relationship is different at elevated temperatures compared to room temperatures affected the lateral-torsion buckling curve of steel at elevated temperatures. In addition, the elastic modulus decreases faster compared to the yield strength at elevated temperatures. The study found out that residual stresses at elevated temperatures do not highly affect the buckling resistance of steel beams. This arose due to smaller difference between residual and yield stresses at elevated temperatures (Mirambell, & Real 2000, p. 109).
Based on the design procedures contained in Eurocode 3, part 1.3, Ranby (1999, p. 35) developed a method for determining the buckling resistance in steel fire designs. In this method, the designer applies the equations of Eurocode 3 for the calculation of buckling resistance in fire designs after considering the reduction of mechanical properties of the material and the buckling performance of the material in the finite element analysis (Young, &Yan 2000, p. 11). Ranby’s study involved steel wall studs.
Conclusion
Unlike carbon steel, the stress-strain relationship of stainless steel is non-linear with no clear yield point. To establish the stress-strain relationship of stainless steel, engineers use the steady state and transient-state tests. These tests evaluate the mechanical properties of steel such as the elastic modulus, the yield strength, and the ultimate tensile strength. The properties enable the structural designers to understand the behavior and the stress-strain relationship of steel under fire conditions.
Different studies have proposed various models for predicting the failure temperature and the buckling modes of steel at elevated temperatures. Using the stress-strain curves, the analysts can model the behavior of steel under fire conditions to determine the mechanical properties of steel at such elevated temperatures in order to predict whether it can withstand additional increase in temperature. Engineers usually use insulation materials to protect Steel structures from fire. The stress-strain relationship provides for determination of the steel’s ability to withstand elevated temperatures, which is important in designing fire design models of stainless steel.

Reference List
Ala-Outinen, T., 1996. Fire resistance of austenitic stainless steels Polarit 725 (EN 1.4301) and Polarit 761 (EN 1.4571). VTT research notes. pp. 14-25
Ala-Outinen, T., & Oksanen, T., 1997. Stainless steel compression members exposed To Fire. VTT research notes, pp. 21.
Alfawakhiri, F., & Sultan, M., 2000. Fire resistance of load-bearing LSF assemblies. Fifteenth International Specialty Conference on Cold-Formed Steel Structures, pp. 73
Buchanen, A., Moss, P., Seputro, J., & Welsh, R., 2004. The effect of stress–strain Relationships on the fire performance of steel beams. Engineering Structures, 26(11), pp.1500-06.
Caldwell, J., 1965. Ultimate Longitudinal Strength. Trans. RINA, 107, pp. 411-14.
Cheaitani, M., & Burdekin, F., 1993. Ultimate strength of cracked tubular joints. Proc. 5th International Symposium on Tubular Structures, pp. 21-23.
Chen, J., & Young, B., 2004. Effects of elevated temperatures on the mechanical Properties of cold-formed steel. Engineering Structures, 25(16), pp.138-41.
Chen, J., & Young, B., 2005. Stress–strain curves for stainless steel at elevated Temperatures. Engineering Structures, 28 (5), pp. 229-239
Drysdale, D., 1999. An Introduction to Fire Dynamics. London: John Wiley and Sons.
Eurocode 3 (EC3), 2001. Design of steel structures – Part 1.2. General rules – Structural fire design. Brussels: European Committee for Standardization.
Feng, M., Wang, Y., & Davies, J., 2001. Behavior of cold-formed thin-walled steel short Columns under uniform high temperatures, Proceedings of the International Seminar on Steel Structures in Fire, pp. 65.
Guedes, C., Gordo, J., & Teixeira, A., 1998. Elasto-plastic behavior of plates subjected To heat loads. Journal of Constructional Steel Research, 45(2) pp. 179-83.
Hautala, K., & Schmidt, H., 1998. Buckling of Axially Compressed Cylindrical Shells Made of Austenitic Stainless Steel at Ambient and Elevated Temperatures. Bericht 76: Universität Essen.
Iso-Mustajärvi, P., & Inha, T., 1999. The fire protection of load-bearing steel structures. Journal of Constructional Steel Research, 53(6), pp. 59-62.
Klippstein, K., 1978. Strength of Cold-Formed Steel Studs Exposed to Fire. Proceedings Of the Fourth International Specialty Conference on Cold-Formed Steel Structures, pp. 89.
Lee, J., Mahendran, M., & Makelainen, P., 2001. Buckling Behavior of Thin-Walled Compression Members at Elevated Temperatures. Sixth Pacific Structural Steel Conference, pp. 17.
Mirambell, E., & Real, E., 2000. On the calculation of deflections in structural stainless Steel beams: an experimental and numerical investigation. Journal of Constructional Steel Research, 54(1), pp. 109-14.
Myllymaki, J., 2001. Fire tests on cold-formed bare and protected SHS compression Members. VTT Building and Transport, Fire Research, p. 8.
Nylander, H., 1956. Torsion, Bending, and Lateral Buckling of I-Beams. Transactions of The Royal Institute of Technology, pp. 7.
Outinen, J., Kaitila, O., & Makelainen, P., 2000. A Study for the Development of the Design of Steel Structures in Fire Conditions: Structures in Fire. Proceedings of the First International Workshop, pp. 6-15.
Outinen, J., & Makelainen, P., 2001. Effect of High Temperature on Mechanical Properties of Cold-Formed Structural Steel Tubular Structures IX. Proceedings of the Ninth International Conference on Tubular Structures. pp. 1-5.
Ramberg, W., & Osgood, W., 1973. Description of stress–strain curves by three Parameters. NACA technical note, pp. 17.
Ranby, A., 1999. Structural Fire Design of Thin Walled Steel Sections. Division of Steel Structures, pp. 31-35.
Rasmussen, K., 2003. Full-range stress–strain curves for stainless steel alloys. Journal Of Constructional Steel Research, 59(1), pp. 45-49.
Rasmussen, K., 2006. Full-range Stress-strain Curves for Stainless Steel Alloys. Advanced structural engineering, 81, pp. 1-41
Rhodes, J., 1991. Design of Cold Formed Steel Members. London: Elsevier Science Publishers Ltd.
Sakumoto, Y., Nakazato, T., Matsuzaki, A., 1996. High-temperature properties of Stainless steel for building structures. Journal of Structural Engineering, 122(4), pp. 397-99.
Thonton, E., 1993. Thermal buckling of plates and shells, Applied Mechanics Revue, no 10. American Society of Mechanical Engineers, 6, pp. 485.
Uy, B., & Bradford, M., 1994. Inelastic local buckling behavior of thin steel plates in Profiled composite beams. The Structural Engineer, 72 (16), pp. 258-62.
Uy, B., & Bradford, M., 1995. Local Buckling of Cold Formed Steel in Composite Structural Elements at Elevated Temperatures. Journal of Constructional Steel Research, 34(5), pp. 50-55.
Young, B., & Rasmussen, K., 1998. Design of Lipped Channel Columns. Journal Of Structural Engineering, 124(2), pp. 139-141.
Young, B., &Yan, J., 2000. Finite Element Analysis of Cold-Formed Channel Columns. Fifteenth International Specialty Conference on Cold-Formed Steel Structures, pp. 11-16.