Background
This research was conducted to provide detailed information on system development with special emphasis on queuing theory. The introduction is an overview of interactive processes to system development, system efficiency, and the Markovian distribution model. Theoretical and practical approaches to system design and in particular practical situations where customers waited for long in a queue to be served formed the basis of the research.
Of interest was the waiting time a customer spent in a queue to be served in the post office. Customers who called in at the post offices experienced the problem of staying for many hours in long queues before they were served. In particular, the focus was on service provision by post office clerks. The time taken by a clerk to serve a customer determines a customer’s contribution to the business.
Despite the fact that several factors determined customer service rates, the basic ones included customer arrival time, customer service time, the state of the queue whether empty or occupied and the number of servers. The possibility of designing a system that works efficiently by maximizing available resources while improving system performance was key to conducting the research. A cost-effective model could be recommended based on the research for performance enhancement and resource optimization.
Problem
The researcher identified the problem of time spent by customers waiting in a queue to be served to be too long translating to a loss of time and income. This translated to customer dissatisfaction, inefficient resource utilization and allocation, poor system performance, and loss in profits due to reduced customer and clerk contributions to the business.
Objectives
The main objective was to identify system variables that could be manipulated to achieve the following:
- Effective resource allocations
- Resource optimization
- Improved system performance
- Increased employee contributions
Introduction
System engineering is an interdisciplinary approach to system development incorporating interactive activities in system development. These activities provide an overview of the scope of system engineering activities. System scope activities include system life cycle integration, planning lifecycle, development phases, system baselines, system engineering processes, integrated teaming, and system engineering management. System elements interact to achieve a system’s objectives. System efficiency, therefore, counts on the ability of a system to optimize its resources in minimizing service time spent on a job or customer.
Customer arrival times are distributed randomly, but waiting and service times can be analyzed based on data collected from the post office case study. To efficiently provide services for customers, customers are served in a queue. This research is based on analyzing queuing systems with special emphasis on M/M/1 queuing model (M/M/1 Queueing System 1).
Systems can be designed after several models, but the M/M/1 model is the simplest model which relates to practical aspects of life and provides sufficient information on decision making on the best method to adopt. The model provides a mathematical approach to understanding system performance. The diagram below illustrates the nature of interactions and parameters integrated into system development and the flow of data or interaction from one system element to another.
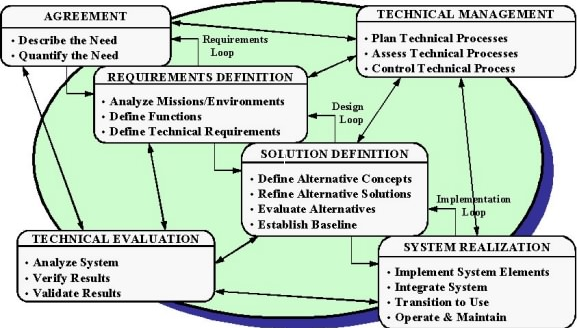
Queuing Theory
This mathematical approach to using the M/M/1 model is based on the Poisson distribution where a customer joins the back of a queue, waits in the queue as it advances, then gets served and leaves the queue at the front. This approach provides critical information on how to model an efficient system while bearing in mind system performance and resource optimization. Poisson distribution is a discrete event distribution with singly distributed events separated by discrete time intervals.
According to the article, M/M/1 Queueing System (1) independent events occur randomly with the same probability distributions. The Poisson distribution is mathematically expressed as: P(x) = µx · e-µ ÷ x! (Where x is the number of times an event occurs).
Theoretically, suppose on average customers arriving at the post office at a point in time are 60 and the interarrival time is one minute, in a space of one hour, then the probability that the interarrival two customers arrive simultaneously is given a by the mathematical solution: Values assigned are, µ = 1(interarrival time), and x = 2 (the number of customers), then P (2)=e-1/2!=0.3679÷2=0.1839.
In this case, the researcher first focused on an M/M/1 model. According to the article M/M/1 Queueing System (1), a single severs assumptions include:
- Time spent on servicing any individual customer was negligible compared to the number of customers in the queue.
- No customer influenced another customer in using a particular queue, therefore, events were independent
- Customer population in the queue was always big.
Assumptions
- Customers came and joined the queue from the back.
- Customer arrival time was modeled after a Poisson distribution
- Service time can be accurately measured
- There is the probability that a queue can be empty or full
- Data provided about customer service time is accurate
- The efficiency of the server remains the same all through the study
- No customer will jump the queue (no priority queues)
- The service time has an exponential distribution
- No stochastic variables
Data Collection and Validation
Data collection formed an important component in conducting the research. The researchers considered two sources of data, primary data and secondary data. Qualitative and quantitative aspects of the collected data were considered. Quantitative data was randomly collected as it fits a Poisson distribution (M/M/1 Queueing System 1). Quantitative data collection using this technique depended on the situation on the ground. Situational factors included customer behavior, number of servers, average arrival time, average waiting time, the length of the queue, and system performance.
Primary data collection
The researcher identified data collection through observations as the best viable method among the many alternatives available. The researcher did the work of collecting actual data using appropriate data collection instruments. This data was quantitatively based on the fact that numbers were generated from the research study. The observations were well-defined occurrences. Borysowiech (1) sees the advantage of this data collection method as a first-hand way of obtaining information. Document reviews formed a qualitative approach to data evaluation.
Observations formed an important part of the research. Several advantages were identified with this data collection approach. The researcher provided detailed information about the elements to be observed during the research study based on a structured approach. The research method was characterized by personal observations. However, the researcher could not manipulate system variables to a great extent. In addition, the researcher played the role of participant-observer at some point in time in the process of data collection.
The research required long-term data collection. This was an important aspect of the research since long-term data was one of the methods of verifying the validity of data collected during the research study by performing validity tests. In addition, varieties of data could be analyzed to determine system behavior with different sources of data. In addition, observation was identified as a cost-effective method of data collection and was identified to be within the financial capabilities of the researcher.
Data was easily obtained from the post office clerks on previous researches on the topic in question and the clerks positively cooperated on the issues of data collection and timing. Customers who participated in the study were informed about the need to collect and the data in relation to queuing which could form an essential part in analyzing service time distributions and system performance. Customers were very supportive of the event and were non-obstructive.
Secondary data collections
In addition to using primary data, secondary data was a vital component in influencing the results of the research study. Secondary data could be made available upon request from post office authorities, journals and books.
Data recording
The researcher planned beforehand on appropriate methods of recording collected data to ensure that data was entered accurately as these data could be relied upon in decision making and for future research.
Data Validation Techniques
Data made available from the observations must be reliable and be the actual data needed for the research study in question. The researcher undertook to ensure the validity of the data and whether the data actually reflected on the research study in question. Emphasis was placed on the validity and reliability of the data. A triangulation test was conducted to identify the degree of reliability of the data.
Data validation and verification were also based on the degree of accuracy of definitions provided by the researcher. These data had to be consistent with the definitions provided by the researcher. This was confirmed by checking and counter-checking the collected data and identifying corrupt and missing data.
Reliability checks
Reliability checks were done on the data to determine if other researchers could obtain the same results using the same instrument of data collection. In this case, the data collection instrument was observations. Consistency tests were done on the collected data for reliability.
Validity
Validity checks provided accurate information on whether the researcher obtained the right data to address the research problem. In addition, validity checks were tools that helped determine whether the researcher had access to system variables. For the research in question, system variables included queue length, customer service time, customer inter-arrival time, customer waiting time, system state, and a number of servers.
According to Wolff (2) validation and verification checks conducted were based on batch and interactive methods where data was double-checked and double data entry checks were key in determining the degree of accuracy and reliability of the collected data. This method ensured that errors could be traced and corrections could be done on the data.
Models and Analysis
Different queuing models are used to provide practical solutions in designing systems and enhancing system performance. They provide approximate solutions to practical problems which reflect on real-life situations which are expressed mathematically. These models depend on a number of steady-state system variables which determine the efficiency of a system commonly referred to as system performance.
These variables include the number of customers in a queue waiting to be served, the time spent in a queue by a customer, statistical distribution of the number of customers and the total time spent waiting for a service, the system state based on the probabilities of being full or empty, and the probability of the system being in a particular state (full or empty) at any time when a customer calls in.
Several notations can be used to denote a system. One such is Kendall’s notations in which standard letters represent particular states. Kendall’s notation can be expressed as A/B/S/K/N/Disc where each letter represents a particular state.
- Time between arrivals
- Time spent in servicing customers
- Number of clerks servicing customers
- Number of customers the system can accommodate
- Number of customers who call in
Disc. Service discipline based on system design and system transition states.
According to Borysowiech this model narrows down to an A/B/S model. Of interest was the emphasis on the M/M/S model where the letters A/B/S are represented by letters M/M/S for a Markovian exponential model. Other system state elements are assumed to take infinity values (K and N) and Disc is assumed to be on a first come first out algorithm.
M/M/1 Queueing System (1) identified service discipline which signifies a situation where customers are served one at a time and the number of clerks at the counter are more than one and the waiting room is assumed to have an infinity capacity. Should the researcher find it expedient to design another queuing model, extra letters must be added to the M/M/S model to accommodate the new model upon which calculations can be based.
Consider a model with a single server and a single queue. Let the customer arrival rate be µ and the average service time be E (B), then work done is equivalent to the product of arrival rate and the average service time (µ E (B). In order to avoid a scenario where the queue grows infinitely long, there was a need to design a system characterized with µ E (B) <1. This could to improved system performance
Maintaining a small occupation rate is generally referred to as server utilization, signifying the time spent by the clerk to serve a customer.
Sensitivity Analysis
Sensitivity analysis provides practical information on the effects of altering system variables and noting the resulting system behavior. These variables include queue length, customer service time, and system capacity (Wolff 34). Of special importance was the behavior of the system with changes in system variables. These variables included queue length, customer service time or time spent for the customer to wait in a queue, and other variables already mentioned.
Wolff (37) adds that another important system variable is the number of servers. The researcher wanted to determine the effect on system performance when the number of servers was adjusted upwards or downwards. The effects of upward and downward adjustments were noted.
Conclusions
System engineering is an interdisciplinary approach to system development consisting of interacting elements which work together to achieve system goals and objectives. Efficient systems can be designed after a variety of system models designed to address real-world problems are analyzed. One such system is the queuing and service provisions in the post office. The problem associated with waiting for long in a long queue for service was a problem of much concern for the researcher.
Queuing models depend on system variables which include customer occupational rate (inter-arrival time and service time), number of customers in a queue, number of servers (number of serving clerks at the counter), the probability of a certain system state (queue empty or occupied), length of a queue, average service time in addition to elements which characterize a queue. These elements include customer arrivals, customer behavior, customer service time, system capacity, waiting for space, and service discipline.
Recommendations
Much detailed research needs to be conducted on various system designs and queuing models besides the M/M/S model by the researcher to compare various system performances under different queuing models. This could yield more information which could enhance decision-making in efficient resource allocations and system optimization.
P = (ù/µ) where ù= mean, µ= average service rate, p= occupancy or service rate.
N=p/ (1-p) where N= average no of customers in a queue, (time in minutes)
Works cited
Borysowiech, Craig: Observations from a Tech Architect: Enterprise Implementation Issues & Solutions. 1998-2010. Web.
M/M/1 Queueing System. 2000-2009. Web.
Wolff, Ronald, W. Stochastic modeling and the theory of queues, Prentice-Hall, London, 1989.