Investigating Number Systems Report

Prior to comparing Hindu-Arabic and Babylonian numeral systems, it is of the crucial importance for us to give the definition to such notion as number, because it can be interpreted from several points of view. In this case, we should discuss it as a symbol, which is used to represent quantitative characteristics of any phenomenon, such as for instance, amount, size, weight, speed etc(Corbett, 200). Thus, number system is a set of such symbols.

However, its role should not be limited only to representation, number system also include certain operations: addition, subtraction, multiplication, division etc. It should be taken into consideration that not all of them allow these operations most due to the complexity, which makes any them practically impossible or time-consuming. In this report, we will try to compare decimal and sexagesimal numerical systems.

Overall, we can say that there is a great variety of numerical systems, though all of them were practically replaced by Arabic digits that are now considered the most convenient not only for representation, but for mathematic operations as well. Among the ancient nominal systems, we can single out the following ones: first, unary number system (which was once used in ancient China and Japan. If we want to represent a certain number, for example 7 and we need to take a certain digit or probably it would be better to say symbol and repeat it seven times. With help of such system, we can easily add or subtract, however, division or multiplication are very difficult.

Furthermore, we should mention the so-called sign-value system (especially Roman Numerals). Babylonian numeral systems can be classified as position-value notation, which means that the value of the value of the symbol or digit depends upon its position in the number, for example, it may represents units, tens, hundreds etc. Among such systems we should mention Babylonian and Hindu-Arabic digits, though there is a considerable difference between them(Georges Ifrah, 2000).

In this report, we will focus on Babylonian numerals and their peculiarities. First, it is worth mentioning that it is based on the relationships between the position of the digit and its value, in other words it is a position value system. At some point in history, such form of numerical representation was almost a breakthrough because before the arrival of Babylonian numeral, people had to employ original symbols for each number, which made any form of calculation almost impossible or they had to use unary system, which was also very impractical. Nevertheless, we should say that Babylonian numbers are not entirely original in, because they employ the principles of older systems, for instance, we can take such number as four, it can be represented in such way:

. In this respect, it is necessary to mention that Babylonian equivalent of Hindu-Arabic digit 1 (one) looks like this:

The remnants of the most ancient unary system are still very noticeable in Babylonian digits. Unlike it, Hindu-Arabic numeral system does not require these unnecessary symbols, which makes it much more applicable for mathematical operations(Feferman, 2003).

Babylonian numerical system is based on the so-called cuneiform script, which consists of wedge-shaped symbols. Probably it would be better for us to illustrate it, for instance the number thirty four looks in the following way in Babylonian digits:

. This sign represents tens; it can be observed that it is tripled. Naturally, in comparison with some other ancient systems, Babylonian digits are relatively simple; however, they are no longer applicable, if we are speaking about large numbers. For instance it we take such number as two thousand three hundred and nine. In Babylonian numeral system may look in the following way:

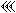
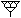
In sharp contrast with Babylonian numbers, Hindu-Arabic numeral system employs only ten digits, while its counterpart has sixty symbols. On the one hand, we can speak of certain similarities between these two systems. First of all, the position of digit also determines its value. However, it is much easier than Babylonian system. First, one should bear in mind that at the core of Babylonian numerical system lays the number sixty (Corbett, 2003); Graphically, it looks like this: for instance, if we use these digits, the number two hundred and thirty nine (239), will be presented in this way:

.

While analyzing the components of this number, we should pay extra attention to the peculiarity of Babylonian numerical system. First, as it has been mentioned before, it is sexagesimal, which means that at its core is the number 60. The main problem is that 1 and 60 are represented in an identical way; this is the main cause of confusion. In our case, the combination of symbols denoted

sixty, multiplied by three, plus 10 multiplied by fiveand plus nine.

It is now considered that the main disadvantage of Babylonian numerical systems that it could both decimal and sexagesimal which means that it could be based on 10 and on sixty. Perhaps it is necessary to illustrate this statement. We can take such number as thirty one. It is interesting that thirty two or thirty three differ from its predecessor only by one symbol. At the core is the number 10, However, we take such number as 81, Babylonian digits become sexagesimal, for example. It can be interpreted as 60 plus twenty and plus one.

It should be also pointed out that Babylonian numerical system did not have any representation for zero. Naturally, such notion as nothingness or absence of any quantity was known to them, but it was not shown seen only as the absence of any digit or merely space. The main problem is how to differentiate between numbers for instance in Hindu-Arabic numeral system, this digit show the difference between units and tens, for example, 6 and 60. It is impossible to see it in Babylonian number system. Overall, we can say that this system has left some trace in the modern system of measuring, though we often fail to see it. For instance, it is still widely used in geometry, especially in trigonometry. Apart from that, the measurement of time is still based on sexagesimal numerical system.

Thus, having compared Hindu-Arabic and Babylonian number systems we arrive at the following conclusions: first, Babylonian numerical system is based on sixty elements, whereas Hindu-Arabic has only 10 digits at its core. Secondly, it does not have any representation for zero (or nothingness), which also presents us with some difficulties. Furthermore, in its core, the Babylonian number system is still based on unary measuring or simply repetition of the same symbol. Nevertheless, the main problem is that Babylonian numerical system can be both sexagesimal and decimal, which was probably the main reason why it was substituted by Arabic digits.

Bibliography

Georges Ifrah (2000). The Universal History of Numbers: From Prehistory to the Invention of the Computer. John Wiley & Sons.

Greville G. Corbett (2000). Number. Cambridge University Press.

John Derbyshire (2001). The Unknown Quantity: A Brief History of Algebra. National Academies Press.

Solomon Feferman (2003). The Number Systems: Foundations of Algebra and Analysis. AMS Bookstore.

Terence Hugh Jackson (1975). Number Theory. Routledge.