Introduction
The modern high-tech world allows humankind to receive and practically use the most progressive solutions, which were scientific and engineering consciousness development products for many centuries. Although the current academic community issues are becoming narrowly focused, a more detailed study of already known concepts is fundamentally important, as it allows to preserve and transmit useful information through generations. Moreover, even in spite of the apparent development of fundamental mathematics, many of its models reveal an intriguing presence in nature, and thus additional analysis can be classified as interdisciplinary research of the world order.
The deep study of mathematical patterns allows the student not only to gain new knowledge about scientific concepts and expand the available information but also to systematize and structure the already known information. Thus, thanks to the written works, the student has the opportunity to collect divided data on mathematical models — be it progressions, arithmetic operations, or the laws of algebra — into a single whole, conducting reflexive activities. In other words, works in which it is necessary to parse the selected problem in detail are useful for both the reader and the author at the same time. This is especially important if the research topic is directly related to the material that was disassembled during the semester: it will allow using skills of critical and logical thinking to collect new useful information.
The topic of the Fibonacci sequence, which is a recursive set of numerical data, was chosen as the focus of the research in this paper. The choice of a specific question was primarily due to the increased interest in the concept since it is known that Fibonacci numbers are not only used in arithmetic mathematics but also in art, construction, and biology. Thus, it was important to perform a critical analysis and determine the features and properties of this sequence, including to justify its presence in various, amazing spheres of life. Moreover, it was necessary to introduce a classification of known mathematical sequences and determine what their recursiveness proved. Finally, an important question of this research paper was a brief description of the life and work of Leonardo of Pisa, known in science as Fibonacci, who became a central figure in the mathematics of medieval Europe. For this reason, this work aims to collect and summarize useful data on the Fibonacci sequence and related mathematical concepts.
Fibonacci Sequence: The Definition
Turning to terminology, it is worth determining that the Fibonacci sequence is called a recursive numeric series of data, each of the subsequent terms of which is dependent on the previous one. In other words, there is a mathematical connection between all the elements of the series, which means that one can expect that there is a certain formulaic pattern that allows determining a specific member of the sequence, knowing only some of the necessary and sufficient data. Thus, given the Fibonacci sequence’s infinity, it is possible to identify the hundredth, thousandth, or even millionth number using formula models.
It should be recognized that historically this sequence was discovered by the European mathematician Leonardo of Pisa, who simulates the development of a population of rabbits isolated from the environment (Sweet 2017). It follows that the nature of this concept is not originally purely mathematical but cross-profile. Thus, the medieval mathematician studied the dynamics of the idealized animal population — since biologically, such models are unlikely — assuming several important conditions. First of all, a pair of rabbits, male and female, were placed in an isolated environment on January 1 so that a month later (on February 1), they make a new pair of rabbits, but never die. When trying to assess the progress of pairs of rabbits during the year, the scientist received the following sequence.
1,1,2,3,5,8,13…(1)
Herein, each of the terms described the number of actual pairs of rabbits for a particular month. Therefore, if there were only two rabbits (or one pair) in January, then by the third month, the number of animals in the population will reach four, which is equivalent to two pairs, as shown in Figure 1. Consequently, at the end of month n, the number of pairs of rabbits will be equal to the number of pairs in the previous month plus the number of newborn pairs, which will be the same as the number of pairs two months ago. Formally, this can be written as (2): Fn=Fn-2 + Fn-1 (2)
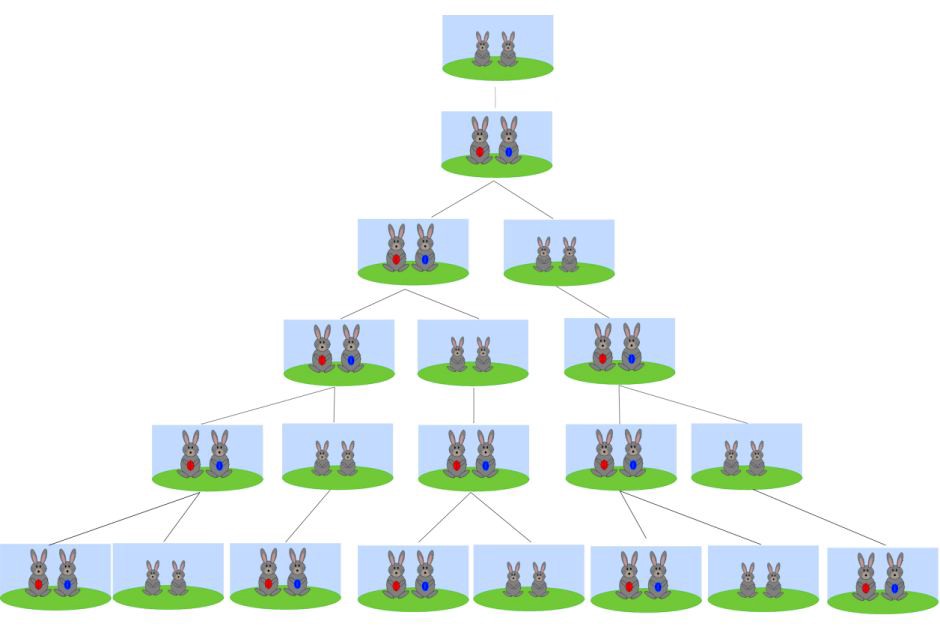
Summarizing the above information, it should be specified separately that using zero at the beginning of a sequence is optional because some authors may recognize this necessity while others do not. In the second case, the sequence should start with one. Conversely, if one considers the classical Fibonacci sequence standard, the first term is zero, as shown in equation (3).
0,1,1,2,3,5,8,13,21,34,55,.. (3)
1=0+1 (3.1)
2=1+1 (3.2)
3=2+1 (3.3)
As can be seen, each subsequent term was obtained by adding the two previous ones. It is important to clarify that although the numerical sequence initially indicates a quantitative measure of pairs of rabbits in an isolated environment, it may theoretically contain negative values too. They can be determined by using an equivalent form for calculation, as indicated in equation (4). In this case, each odd negative term of the sequence, due to the peculiarities of the exponential formula, will have a positive sign, while the even term has a minus sign.
F-n = (-1)n+¹Fn
Consequently, the general numerical sequence with both negative and positive values is symmetrical concerning zero and can be written in the form of Table 1.

In the ongoing research, it was found that this numerical sequence has a number of remarkable properties, including the ability to predict a specific member of the series, using the function of value from the number of the element. As already mentioned, it is possible to identify specific numerical values standing in the specified places of the series using the formula (5). In general, this pattern is called the Binet formula, known in the mathematical community as a scientist who contributed to matrix algebra, equation algebra, and rotating-body mechanics (Webb 2017; Krishnan 2020). In this formula, it is also interesting to note that the first in the fractional numerator expression is commonly referred to as the Golden Ratio.
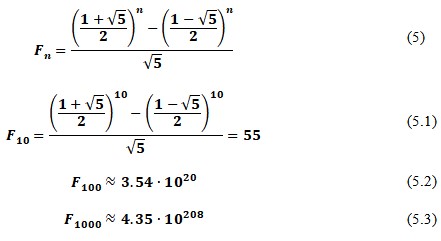
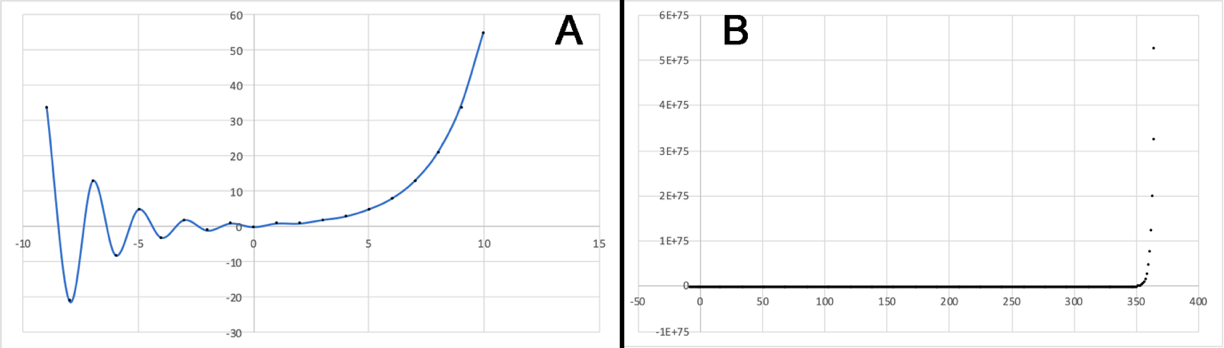
The rapid growth of numerical values within the first thousand members is a confirmation of the hypothesis that this sequence is exponential. The detailed representation of the first members of the numeric sequence as a function of the element number shows the rapid growth in the area of positive numbers and oscillations with increasing amplitude for negative numbers. Scaling the graph to several hundred allows estimating that starting from the 350th elements of the row, the sequence’s values significantly progress (Fig. 2).
However, some additional mathematical properties of the Fibonacci sequence must also be marked. Since this numerical series is a classical progression, standard arithmetic operations such as summation or subtraction can be performed. For example, equation (6) shows the sum of the first terms of a sequence, and equation (7) shows the sum of only the odd members. The sum of even terms is shown in equation (8). It is also interesting to note that each previous term’s ratio to the subsequent one always tends to be 0.618: equation (9).
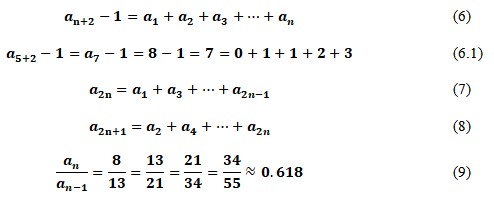
Identification of Recursive Sequences
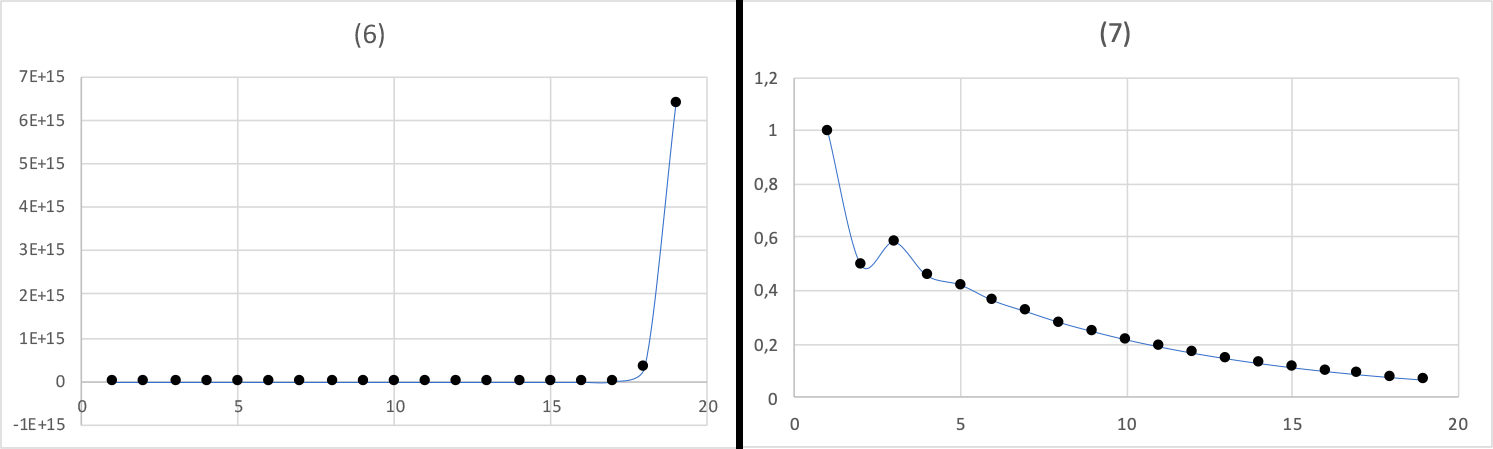
Recognizing the Fibonacci number series as a recursive sequence, special attention should be paid to a particular explanation of this term. Encyclopedically, recursive refers to any phenomenon in which there is a return to the past or previous (Dean 2020). In the context of mathematical models, recursive functions are those in which the value of the next argument depends on the previous one. The values of the arguments standing on specific numbers can be predicted using a formulaic dependence. However, for the calculations to be successful, it is necessary that for some arguments (usually, the first members), the function is set non-cursively. Equations (10)-(11) give two examples of recursive dependencies that are not a Fibonacci sequence. The graphical representation of recursive functions does not necessarily have to be subjected to any trend, as shown for the equations in Figure 3 below.
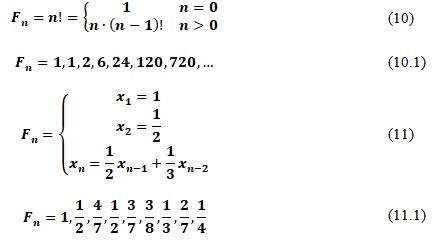
Practical Application of Fibonacci Sequence
It is fair to note that this numerical series pattern was discovered even before Leonardo and was actively used by the ancient Greeks and Egyptians in solving applied problems. It follows that mathematical reopening of a sequence actually means finding symbolic dependencies that would satisfy a sequence occurring in natural phenomena. Indeed, in nature, architecture, fine arts, mathematics, physics, astronomy, biology, and other fields of knowledge, regularities described by Fibonacci terms were found (Palazzo 2016). It is significant to determine in advance the nature of the association between the Fibonacci sequence and the Golden Ratio. The second is usually characterized as a two-value relationship where the larger value refers to the smaller value, as shown in equation (12).
a/b=a+b/a
The geometrical idea of such a concept consists of the division of the AB segment by point C into two parts that satisfy the condition presented in figure 4. Numerically solving this equality, one obtained the expression (13), which is called the Golden Ratio (Mann 2019). It is interesting to note that this ratio is also related to the Fibonacci sequence: each successive term divided by the previous one quantifies the Golden Ratio, while the reverse procedure gives the opposite value. In addition, the graphical arrangement of Fibonacci numbers on a rectangle as a sum of squares, so that each side is equal to the sum of the sides of two smaller squares (fig. 5), gives the sequence the form of a harmonious spiral.
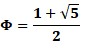
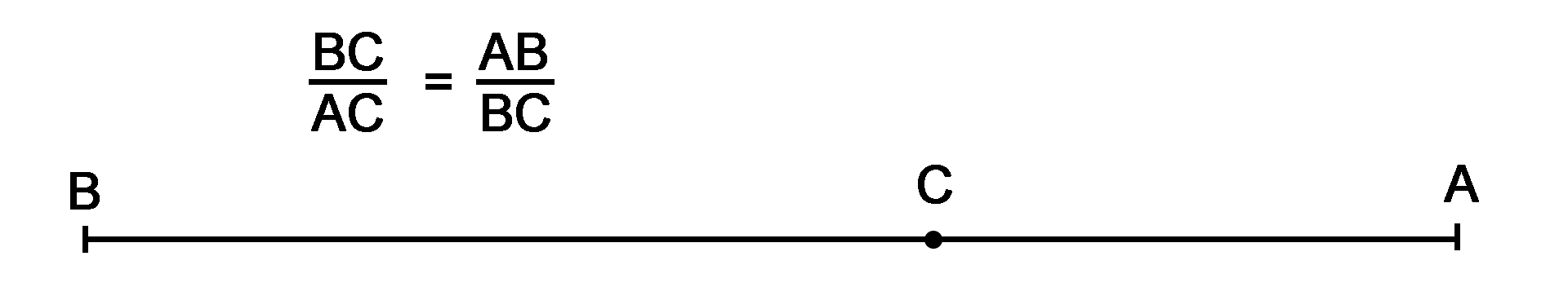
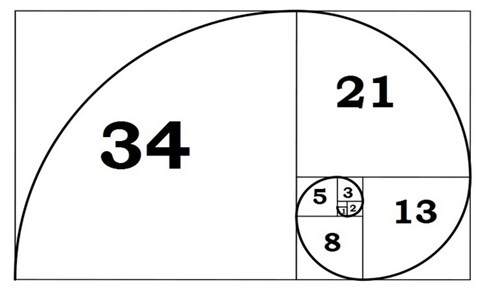
As it was said, amazing examples of the combination of the Fibonacci sequence and Golden Ratio can be found in many different areas of life. In order to simplify the organization of submitted information, it is reasonable to place the examples in Table 2.
Tab. 2. Examples of application Fibonacci numbers.
Brief Biography of Leonardo of Pisa
The mathematical description of the Fibonacci sequence’s amazing nature was made possible thanks to Leonardo of Pisa, an Italian mathematician from the Middle Ages. The name of Fibonacci was invented in 1838 by the historian Guillaume Libri. Leonardo was born in about 1170 to a family of merchants, so from childhood, the man became acquainted with the skills of Arabic account (Gies 2020). In his perhaps most famous mathematical work, Liber Abaci, he first described a numerical sequence, using an example of a population of rabbits. Thus, the man was able to popularize his discoveries, for which the Italian authorities awarded him.
The first of the developed sequences is tied to the biological principle of division of the protozoa microorganisms under favorable conditions. The standard of such reproduction is mitosis, a process that results in two daughter cells from one single-celled animal. Knowing this, it is possible to create the following sequence (A):
F=1,2,4,8,16,32,64 (A)
An attempt to write a given number series of numbers in a formula leads to a pattern presented in equation (B), where d is an increase in the number of strains per unit of time:

Therefore, using this formula, it is possible to predict the population’s development during a certain number of divisions. For example, calculations of the number of microbial individuals for 2, 10, 100, and 1000 divisions are presented in equations (C)-(F).

Another amazing example of sequences is the decay of a radioactive substance as a function of time. It is known that every certain period — half-life — the number of cores of the matter is halved. So, if the original number of Uranium-238 nuclei in nature was, for example, 1,000,000, then the following dynamics are characteristic:
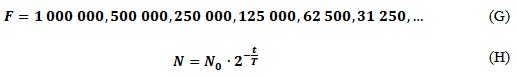
So, using the formula of half-life (H), it is possible to estimate how much Uranus will remain after ten consecutive divisions (one half-life takes 4.5 billion years):
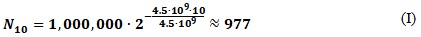
References
Dean, Walter. 2020. “Recursive Functions.” Stanford Encyclopedia of Philosophy.
Gies, Frances Carney. 2020. “Fibonacci.” Britannica. Web.
Krishnan. 2020. “Deriving and Understanding Binet’s Formula for the Fibonacci Sequence.” Medium.
Mann, Adam. 2019. “Phi: The Golden Ratio.” Live Science. Web.
Palazzo, Benedetta. 2016. “The Numbers of Nature: the Fibonacci Sequence.” School Energy.
Sweet, Sarah. 2017. “The Rabbit Hole of Fibonacci Sequences, Recursion and Memorization.” Sarah Sweet. Web.
Webb, Chris. 2018. “Calculating any Term of the Fibonacci Sequence Using Binet’s Formula in C.” Code Drome.