Introduction
Panel data is a two-dimensional array in which one dimension is “spatial” (1 < i <N) and the other is temporal (1 < t <T). Thus, panel data has two indices (i, t). Similar arrays occur when collecting data on a given set of objects over a period (Mummolo & Peterson, 2018). For example, when conducting a survey, there may be “exhaustion” of the sample: someone moved, someone died, someone refused to participate in the survey. In general, the panel data regression follows: xit = Zitαit + εit, i = 1,…, N; t = 1,…, T, where i is the index, t is time, αit is the vector coefficient of the unifying variables Zit in period t for the sample unit i (Xu et al., 2018).
Importance of Panel Data Regression
The main feature of static-dynamic information is the dependence of observations. Dependency is not only the levels of the dynamic series but also the rows (both spatial and temporal) since the membership of the standards to a row is fixed (Zyphur et al., 2019). Yet, the dependence between the series of dynamics is the result of spatial variation, which, because of the inertia of the processes, is stored for a specific time (Das, 2019). Spatial row dependency reflects the synchronous dynamics of the metrics across individual objects, driven by common development conditions. Ignoring these features of the database model leads to erroneous conclusions.
In panel data over a long period, you can identify trends in the development of individual objects and the totality. When the objects are differentiating, but the individual features are stable over the observation period, a fixed-effect model is applied to such an information base (Shi & Lee, 2016). The specific set of such a model is supplemented by the dummy variables of the individual objects u and j, the regression coefficients for these variables characterize the special effects (Zyphur et al., 2019). The pattern of the function y inherent in all objects is considered in the model by the variable t (Okui & Yanagi, 2019). However, due to the uneven development of individual aggregates along with a common trend, different trends may appear significant. Therefore, object periods only extend the model’s information base.
Types of Panel Data Regression
POLS (pooled ordinary least square)
POLS, because of its broad scope, holds an exceptional place among mathematical statistics methods. The POLS task is to evaluate the patterns observed in the background of random fluctuations and to use them for further calculations for forecasts (Ott & Longnecker, 2016). A unique role is played by POLS in geophysics, determining the concept and methodology of solving the inverse problem of geophysics (Balazsi et al., 2015). The POLS problem is solved by parametric estimation of the regression function, which describes the dependence of one quantity Y, whose values (yi) are observed with random errors (θi), on the group of non-random variables X1, X2,…, Xk The regression function is a function of k variables x1 , x2,…, xk, which is the mathematical expectation of Y at X1 = x1, X2 = x2,…, Xk = xk:
f (x1, x2,…,xk) = M(Y/X1=x1, X2=x2,…,Xk = xk).
Fixed-Effect Model
In the fixed-effects model, the unobservable individual effects were correlated with the variables included in the model (Galvao et al., 2020). However, sometimes there are reasons to believe that special effects may not be associated with regressors (Baltagi & Liu, 2016). In this case, individual results can be considered as one component of the error. The formula is:
yi = β0 + β1 xi +εi, if γi −1 < yi ≤ γi ,
where γ0 = −∞, γ1 = 0, γm = +∞, other γj unknown (Shi et al., 2019).
Fixed-effects estimation subtracts time averages from the corresponding variables, and the transformation for a model with random effects subtracts from them the fraction of these time averages, where the proportion depends on σ “, σΕ, and the number of periods T. As a result, the model transforms into Eq (Allison et al., 2017). The regressions remain constant over time, explaining the variables, and this is an advantage of the random effects model over the fixed effects model. The first difference transforms, if the parameter 0 = 1, then the random effects model coincides (Baltagi & Liu, 2016). If the setting 0 = 0, this means that there are no uncorrelated individual variance components in the model, that is, σ “= 0, and the random effects estimate will be reduced to the meaning of the combined model (Cleophas et al., 2018).
Random-effect Model
The random-effects model assumes that special effects do not correlate with the regressors. It is essential to check whether the assumption is valid for such a correlation, which can lead to the failure of most estimates of the model with random effects (Asparouhov et al., 2017). The only exception to this is the intrinsic group estimates of β-coefficients since they are based on a transformation that eliminates the special effect in the model (Cleophas et al., 2018). As a result, the assumption that they do not correlate with the regressors is not related to the unbiased and inability of intragroup estimates. A random-effect model or a random component model looks like:
yit = µ + x’it +αi +εit ,
εit ~ i.i.d. (0,σ2ε);
αi ~ i.i.d.(0, σ2ε),
while αi + εit,
where sit can be considered as a component of a regression error that has two parts: the individual component and i the remaining term sit (Asparouhov et al., 2017). The element i represents an error (random deviation) that is constant over time for the Nth object (Li, 2015). In a random-effects model, the assumptions are made based on the random components i.
Difference Between Types
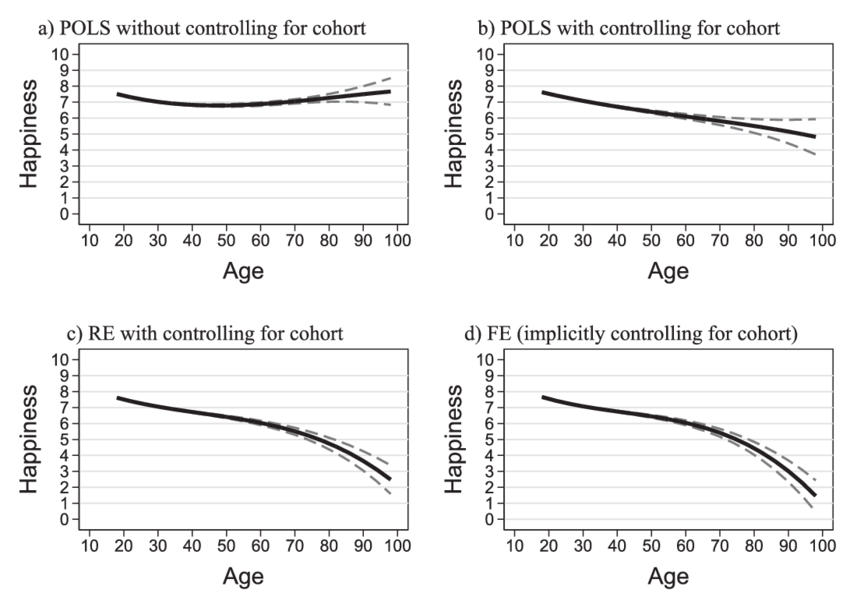
References
Allison, P. D., Williams, R., & Moral-Benito, E. (2017). Maximum likelihood for cross-lagged panel models with fixed effects. Socius: Sociological Research for a Dynamic World, 3. Web.
Asparouhov, T., Hamaker, E. L., & Muthén, B. (2017). Dynamic structural equation models. Structural Equation Modeling: A Multidisciplinary Journal, 25(3), 359–388. Web.
Balazsi, L., Matyas, L., & Wansbeek, T. (2015). The estimation of multidimensional fixed effects panel data models. Econometric Reviews, 37(3), 212–227. Web.
Baltagi, B. H., & Liu, L. (2016). Prediction in a generalized spatial panel data model with serial correlation. Journal of Forecasting, 35(7), 573–591. Web.
Best, H. & Wolf, C. (2015). Fixed-effects panel regression In J. Brüderl, & L. Volker (Eds.). Sage handbook of regression analysis and causal inference (327-356). Sage.
Cleophas, T. J., & Zwinderman, A. H. (2018). Modern meta-analysis. Review and update of methodologies. Springer.
Galvao, A. F., Gu, J., & Volgushev, S. (2020). On the unbiased asymptotic normality of quantile regression with fixed effects. Journal of Econometrics, 216(2). Web.
Das, P. (2019). Econometrics in theory and practice: Analysis of cross section, time series and panel data with Stata 15.1. Springer.
Li, G. (2015). Consistency in estimation and model selection of dynamic panel data models with fixed effects. Econometrics, 3(3), 494–524. Web.
Mummolo, J., & Peterson, E. (2018). Improving the interpretation of fixed effects regression results. Political Science Research and Methods, 6(4), 829–835. Web.
Okui, R., & Yanagi, T. (2019). Panel data analysis with heterogeneous dynamics. Journal of Econometrics, 212(2), 451–475. Web.
Ott, L., & Longnecker, M. (2016). An introduction to statistical methods & data analysis. Cengage Learning.
Shi, J., Boehnke, M., & Lee, S. (2019). Trans-ethnic meta-analysis of rare variants in sequencing association studies. Biostatistics. Web.
Shi, J., & Lee, S. (2016). A novel random effect model for GWAS meta-analysis and its application to trans-ethnic meta-analysis. Biometrics, 72(3), 945–954. Web.
Xu, X., Šarić, Ž., Zhu, F., & Babić, D. (2018). Accident severity levels and traffic signs interactions in state roads: A seemingly unrelated regression model in unbalanced panel data approach. Accident Analysis & Prevention, 120, 122–129. Web.
Zyphur, M. J., Voelkle, M. C., Tay, L., Allison, P. D., Preacher, K. J., Zhang, Z., Hamaker, E. L., Shamsollahi, A., Pierides, D. C., Koval, P., & Diener, E. (2019). From data to causes II: Comparing approaches to panel data analysis. Organizational Research Methods. Web.