Introduction
In today’s supply chain systems wrought with competition, minimal costs and efficient delivery and inventory replenishments should characterize any supply chain system. The proposed system is a multi-echelon multi-period inventory model with the objective of minimizing the overall supply chain cost. In this model, the supply chain is typically defined by a number of network nodes linked together and characteristically defined by a dynamic supply and demand relationship covering a wide geographic location. The dynamism of the supply chain is characterized by varying inventory levels with time at each node.
Here, orders are generated in the most downstream echelon with supply being replenished externally in the most upstream echelon. The main problem is to control the inventory level by optimizing the objective functions in relation to the number of orders in a given period of time. In this case, a robust multi-echelon model provides the most optimal solution to the problem. The rationale of a multi-echelon multi-period inventory system is cost effectiveness, efficiency, and reliability to optimize on the use of nodes.
The Problem Description
The three variables, what should be ordered, the quantity to be ordered, and order period, at each node critically influence the efficiency of a supply chain in a multi-echelon, multi-period, and multi-location or geographically dispersed inventory system (Love, 22). Different nodes play different roles in different supply chains. A comparative analysis of different supply chains reveals several options may be supplied upstream by one or several nodes, or where a series of nodes are supplied upstream and downstream (34) and (Sterman, 55). Typically, in the latter, the series consists of a last node which is subjected to external demand and external supply.
The latter is a description of a typical serial chain. Whitin argues that a network design that optimizes inventory in the current supply chain environment to optimize supply by determining in real time the strategic location and specific inventory levels and requirements in the supply chain is a viable solution (45). However, Cachon, Taylor, and Schmidt argue that multi-echelon multi-period suffer from typical problems such as the degree of uncertainty in customer demands which is strongly correlated with specific methods of determining an accurate size of orders for every echelon in the supply chain for a given period to benefit from an optimum objective function (34) and (Simchi-Levi, Kaminski & Simchi-Levi, 34).
Therefore, uncertainty, time, demand process, and geographic distributions determine to a large extent the optimality and minimization of inventory cost (Cachon and Lariviere, 56). Overly, these are typical control problems that demand due attention and techniques to solve them to optimize the whole supply chain system (Ben-Tal, Boyd, Nemirovski, 35) and (Sterman, 21).
Problem statement
A network of nodes or echelons are geographically distributed in a potential supply chain whose set of supply points are defined as i ∈ I with distribution sites defined by j ∈ J. Suppose the geographic zones for distribution in the supply chain are each defined by k ∈ K, borrowing from the fact that distribution centers can be installed as proposed in the model to include retailing outlets, geographically distributed demand zones, and well defined separation distances between the centers, a cost function is determined and expressed for establishing the points of distribution in the network of nodes (Leemis, 4). Tijms emphasizes that the cost function, as one of the most critical elements in the supply chain is fixed (9).
Wong, Kranenburg, van Houtum, and Cattrysse argue that the whole network is characterized by retailers with a periodic demand distribution using a single sourcing technique where retailing is characteristically defined by a normal distribution defined by I, a mean of i μ, whose variance is φ (10). The nature of the distribution channel is illustrated below in fig 1.

In the above model, the customer demand zone is satisfied by a single distribution point typically characterized by a linear transportation costs (Ben-Tal and Nemirovski, 44). Distribution centers i and j incur linear transportation costs with unit costs C1 and C2 respectively targeting the demand zone, k. In the model, time for demand zones for each customer in the network is well known while deterministic processing time are t1 and t2 respectively. In addition to that, the level of safety stock is defined by safety factors that are α1 and α2 respectively (Tijms, 34). The variables strongly correlate with the standard deviation as noted earlier elsewhere.
The main objective is to determine and design a multi-echelon multi-period inventory model with the objective of minimizing the overall supply chain cost by identifying and determining an optimum number of decision centers, geographically distributed centers, the best linkage or cost effective network between the centers, typical network design to achieve and to meet the main objective, specific service points or plants for specific to meet customer needs and satisfaction, review period, service time, and the safe stock levels meant to optimize efficiency and minimize cost and service time (Lee, Padmanabhan & Whang. 19).
Challenges
Managing a multi-echelon multi–period inventory is a difficult task especially when nodes are distributed across a large geographic location. It has largely been noted that such supply chain systems demand that a regional distribution center be established before other tiers or nodes are replenished for forward distribution. However, the supply chain system is faced with a number of challenges. These include the appropriate level of demand with the correct forecasting to satisfy the demand, the stochastic characteristics of demand, appropriate replenishment frequency to satisfy the demand, and the number of controls for each specific echelon (Terwiesch, Ren, Ho & Cohen, 25).
Approaches
Two approaches were studied to inform the process of creating the model. A multi-echelon approach where the replenishment is split into two sequential replenishment lines was studies. However, it was evidently clear that the approach suffered from critical demerits (Disney, Towill, Van de Velde, 56). These demerits were characterized by lack of visibility when the demand was viewed in the upwards. Thus an inherent weakness included lack of lead time in the nodes. In addition to that, the replenishment lacked the element of clear inventory balance. In addition to that, the system lacked a visibility in the downward demand, was inherently characterized by demand distortions, and difficulties in evaluating network costs (Saab & Corr^ea. 20).
Therefore, it was noted that the proposed model should be inherently characterized by an ability to focus on a single forecasting and avoid multi-forecasting for each specific echelon, lead time variations should be accounted for besides accounting for lead times for each echelon, clear and manageable visibility of the downward and upward demands, and work with clearly synchronized placing of orders (Lee, Padmanabhan & Whang, 19).
Objectives
In modeling the system, a series of objectives were formulated to satisfy the needs for the proposed system. These included:
- To optimize the supply chain system to meet customer needs at minimum inventory.
- To forecast demand and demand variations with near precision.
- To optimize lead times for all echelons in the downstream supply chain.
- To incorporate strategic techniques to minimize the bullwhip effect.
- To ensure that all echelons have completely visible.
- To ensure that minimal costs are incurred at each echelon.
The Proposed System
The proposed model integrates several aspects of a multi-echelon multi-period system. A theoretical and practical analysis of the system will afford to explain the proposed model. In addition to that, it is worth noting that current trends in modeling use computing as a tool in modeling simulations of the supply chain. The proposed system will be analyzed theoretically and a typical case study will be analyzed culminating in a computational view of the simulation.
Multi-Echelon Inventory
Theoretically, upstream and downstream nodes’ inventory levels are influenced by the inventory level of each of the echelons while affecting the lead time of the downstream node. When the inventory of the downstream node is varied, the inventory level of the upstream echelon is equally varied. Thus, the lead time of the downstream node is influenced by the inventory levels of the upstream node and the level of uncertainty in demand.
In the proposed model, stochastic and guarantee service approaches are used to model the system. The stochastic model is a probabilistic approach of dealing with uncertainty and a linear programming problem which characterizes a typically robust optimization model (Ben-Tal, Boyd & Nemirovski, 46). However, it is worth noting that both approaches are quite challenging to model and compute. In addition to that, the proposed model integrates the guarantee service model due to the unique attribute of the approach that allows tactical and strategic decisions to be made in any topological representation.
Typically, the guarantee service model overrides the stochastic model in modeling the system due to its applicability and flexibility for use in a practical setting.
The main idea about the Guarantee service model
Zhang argues that each node, j, in the model is characterized by a guarant tee time T, which combine to by a guarantee time, T, with the aggregate effect of satis fying the demand by downstream customers (34). In order for the model to be efficient, the response time to customer demands will be defined by the relation t + T. Implying that once a customer places a demand for certain goods, and if the time guaranteed for delivery is 1 day, then, the delivery time to optimize customer satisfaction should be at most one day, totaling up to t + T. Typically, efficiency will result from optimization of internal variables that affect the aggregate image and confidence on a supply chain system (Holt, Modigliani & Shelton, 12).
However, exogenous variables that are influenced by market place variables will influence the service time guarantee. In this model, the time t, is the deterministic time for each node in the system and is not influenced by the size of the placed order. In addition to that, the model assumes that the aggregate time for processing an order, processing all materials necessary for the whole handling process, the period spent in transporting the customer’s order, and time for reviews, is input variables in the model before satisfaction for a specific demand is met. It will, however, be possible to determine the replenishment lead time that is strongly related to the aggregate time to make the shipment for a specific demand ready.
The aggregate time will be determined in the model by direct processor time tagged as T-1. The direct processor time in the model is the aggregate of the processing time for the order from the time it was placed and the processing time (Niranjan, 55). The processing time, t, is the sum total of the review transportation, and service or handling period. It is possible to model the net lead time for a specific echelon, for example, node 1.
Therefore, the net lead time for node 1, from the above description is defined in relation to and in terms of the safety stock levels and the varying levels of demand. In that relation therefore, the difference between the guarantee service time and the replenishment time is defines the net lead time for the earmarked node, a concept applicable throughout other nodes in the whole system. It is imperative to note that the each demand by the customer at any specific period should be satisfied promptly during the specified time. In the proposed model, one notes that the changes in demand over the whole lead time period needs not be covered. Therefore, the net lead (NLT) time can be mathematically modeled as illustrated below:
NLT= {(T-1)} + t-T. According to the model, node one is preceded by node T-1.
One assumption about the model is that when the replenishment lead time for node one is equal to that of the predecessor node, then no safety stock will be necessary at that time since replenishment from the predecessor node is within the parameters of the guaranteed service time. It is also assumed that when the guarantee service time is registered to be zero, then, the highest safety replenishment stock is held at the designate node (Ben-Tal, Goryashko, Guslitzer & Nemirovski, 34).
Periodic reviews are done under the base stock policy within a single time period throught the whole system for all nodes in the system. It is important to note that under the model, the assumption is that the behavior of demand is mathematically modeled under a normal distribution. That assumption is based on the fact that the parameters of the standard deviation (φ) of the distribution and the mean (µ) are bounded. Therefore, the demand levels the company can afford to economically satisfy given a specific inventory level are influenced by the latter factors. Research from other quarters and in a similar discipline has shown a consistent practice where stocking levels are used to replenish inventory given stochastic demand variations.
The proposed model will accommodate specified inventory levels, meet specific demand variations, and market demand in a specific period to afford customer demand satisfaction. In addition to that, the assumptions are that when demand rises in volume to overwhelm the proposed system, then, different approaches for satisfying the demand are implemented. Such measures include altering order scheduling besides relying on the safety of the available stock.
The Model
The typical model or proposed model is characterized by an inventory system that consists of a three-echelon assembly. The model is characterized by a sequence of activities, product demands that are external and intermediate for any of the upper echelons. The model is tailored to supply fully assembled components to the customer or the supplier. Each stage of the process is defined by a lead time that is associated by activities such as production and assembly. Inherently, the system is characterized by a level or degree of uncertainty.
In creating the model, a number of assumptions are made. It is assumed that demand occurs singly or per unit product, backordering occurs for products that do not meet customer needs, and a first come first served basis will be the strategy to employ in serving customers.
Typically, the model is as illustrated in fig 2 below.
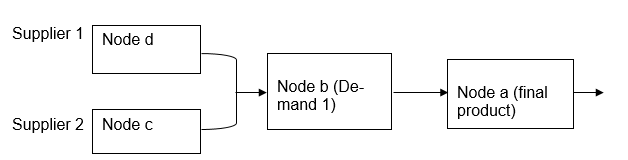
In Blanchard’s consideration of the downstream, the nodes are typically organized in a mathematical relation where each node in the series is identified by N. Therefore, the ith node is identified by any letter or designate number (76). Therefore, i=0, 1, 2,….N-1. It is proposed that each component in the echelon are bought from and supplied by an external supplier and assembled at the subsequent nodes identified in the system as nodes d and c. Further processing of the components provides the final product at node a. In the system, a lead time, l for ordering, and a lead time for manufacturing k, for all the nodes in the echelons for further processing.
Uncertainties are associated with each echelon due to the fact that decisions made at each echelon at any specific period rely on the demand for each echelon and the supply forecasts (Zipkin, 33).
Handling Uncertainty in the multi-period echelon
Many methods and approaches of dealing with uncertainty have been analyzed elsewhere. In the typical environment of the proposed model, the multi-period uncertain linear programming mathematical approach is used (Lin, Wong, Jang, Shieh & Chu, 33). According to Forrester, the main assumption specific to the LP model is that variable used in decision making are determined prior to the actual decision while in other multi-period systems where periods are dynamic, each echelon has decisions made on t>1, where the period is greater that one (9). In the proposed model, historical data will be used in decision making (Kirkwood, 78).
In each of the echelons, the historical data µ will be a function of the decisions of the vectors at each time, t, as argued by (Chen, Drezner, Ryan & Simchi-Levi, 45). Lee, Padmanabhan and Whang assert, therefore, that the most appropriate expression for the matrix P expresses the objective function as shown expressed below (99).
Therefore, µ=µt (Pt), where decision variables are either adjustable or not adjustable. Variables that are not adjustable have are defined by (Pt) not equal to zero and (Pt) equal to zero as argued by (Arrow, Karlin & Scarf, 25).
Conclusion
The multi-echelon multi-period model proposed above is characterized by a supply chain which is typically defined by a number of network nodes linked together and characteristically defined by a dynamic supply and demand relationship covering a wide geographic location. The system consists of a three echelon assembly with periodic replenishments. Precision is achieved by incorporating a linear model for forecasting demand and supply and ensuring that minimum inventory costs are incurred due to the precision used in the forecasting. However, further research will, need to be conducted to determine the behavior of similar models under other variables and with specific multi-echelon systems that have more than three tiers in the system.
Works Cited
Arrow, K.J., Karlin S., Scarf H. Studies in The Mathematical Theory of Inventory and Production. Stanford University Press, Stanford, California. 1958.
Ben-Tal, A., S. Boyd, A. Nemirovski. “extending the scope of robust optimization : Comprehensive robust countairparts of uncertain problems“. 2005. Web.
Ben-Tal, A., A. Goryashko, E. Guslitzer, A. Nemirovski. “adjustable robust solu tions of uncertain linear programs”. Mathematical Programming 99 351-376. 2004.
Ben-Tal, A., A. Nemirovski. “A robust optimization – methodology and application”. Mathematical Programming (Series B) 92 453-480. 2002.
Blanchard, O.J. “the production and inventory behavior of the american automo bile industry”. Journal of Olitical Economy 91.1983.
Cachon, G.P., M.A. Lariviere. “supply chain coordination with revenue-sharing contracts: Strengths and limitations”. Management Science 51(1) 30{44. 2005.
Cachon, G.P., R. Taylor, G.M. Schmidt. “in search of the bullwhip e®ect”. 2005. Web.
Chen, F., Z. Drezner, J. Ryan, D. Simchi-Levi. “quantifying the bullwhip e®ect in a simple supply chain: The impact of forecasting, lead times and information”. Management Science 46 436-43. 2000.
Disney, S.M., D.R. Towill, W. Van de Velde. “variance ampli¯cation and the gol den ratio in production and inventory control”‘. International Journal of Production economics 90 295-309. 2004.
Forrester, J.W. Industrial Dynamics. 8th ed. MIT Press, Cambridge, Massachu setts. 1973.
Hammond, J. Barilla spa (a). Harvard Business School case # 9-694-046.1994.
Holt, C.C., F. Modigliani, J.P. Shelton. “the transmission of demand °uctuations through distribution and production systems: The tv-set industry”. Canadian Journal of Economics 14 718-39. 1968.
Kirkwood, C.W. System Dynamics Methods: A Quick Introduction. Arizona State University. 1998.
Lee, H., V. Padmanabhan, S. Whang. The bullwhip e®ect in supply chains. MIT Sloan Management Review 38 93-102. 1997
Lee, H., V. Padmanabhan, S. Whang. “information distortion in a supply chain:the bullwhip e®ect”‘. Management Science 43 546-58. 1997.
Lee, H., V. Padmanabhan, S. Whang. “comments on information distortion in a supply chain: The bullwhip e®ect”. Management Science 50 1887-93. 2004.
Leemis, L. M. Building credible input models. In Proceedings of the 2004 Winter Simulation Conference, ed. R. G. Ingalls, M. D. Rossetti, J. S. Smith, and B. A. Peters, 29–40: Winter Simulation Conference. 2004.
Lin, P.H., D.S.H. Wong, S.S. Jang, S.S. Shieh, J.Z. Chu. “controller design and reduction of bullwhip for model supply chain system using z-transform analysis”‘. Journal of Process Control 48-499. 2004.
Love, S. 1979. Inventory Control . McGraw-Hill.
Niranjan, Suman. A study of multi-echelon inventory systems with Stochastic capacity and intermediate product Demand. Write state University, 2008.
Saab, J., E. Corr^ea.. “bullwhip eefect reduction in supply chain management: one size ¯ts all?”. Int. J. Logistics Systems and Management 1(2/3) 211-226. 2005.
Simchi-Levi, D., P. Kaminski, E. Simchi-Levi. Designing and Managing the Supply Chain. McGraw-Hill. 2000.
Sterman, J.B. “modeling managerial behavior: Misperceptions of feedback in a dynamic decision making experiment?”. Management Science 35 321-39. 1989.
Sterman, J.B. 2000. Dynamics: Systems Thinking and Modeling for a Complex World. Irwin-McGraw-Hill, New York.
Terwiesch, C., Ren J., T.H. Ho, Cohen M. 2005. “forecast sharing in the semiconductor equipment supply chain”. Management Science 51 208-20.
Tijms, H. C. 1972. Analysis of (s,s) inventory models. Amsterdam, Mathematisch Cen trum.
Whitin, T.M. 1957. The Theory of Inventory Management. 2nd ed. Princeton University Press, Princeton, New Jersey.
Wong, H., B. Kranenburg, G.-J. van Houtum, and D. Cattrysse. 2007. Efficient heuristics for two-echelon spare parts inventory systems with an aggregate mean waiting time constraint per local warehouse. OR Spectrum 29 (4): 699–722.
Zhang, X. 2005. “delayed demand information and dampened bullwhip e®ect”. Operations Research letters 33 289-294.
Zipkin, P. H. 2000. Foundations of inventory management. Irwin Professional Pub. Web.