Project Rules
The trebuchet is a powerful propulsion tool used to launch projectiles of over 500 kilograms in weight through a distance of several meters using a counterweight equivalent to 30 tones. Trajectory projectiles of a trebuchet are precise to the intended target. When designing and constructing a trebuchet, a number of rules are applied in the process specific to a specific project as typically discussed below. In this typical project, the rules include using a counterweight of 4 kilograms that is detachable from the parent machine for the purpose of determining its weight. The project is designed with a center of mass equivalent to 350 mm measured vertically from the base of the projectile. The diameter of the projectile is 66 mm with a weight of 90 grams. The potential energy that is utilized in launching the projectile is from the hanging weight. No other external forces or component part of the system will be mobilized in throwing the projectile except the trebuchet. Each lever shall be on a fulcrum and the number of arms shall not be limited to a specific value (Siano, 5).
Every task performed by the machine shall remain the same to establish its performance and the degree of precision of the projectile. It is important to note that the number of parts to be replaced is limited to one in the period of the completion and part that are replaced should have the same technical specifications as the replaced part. Any contact with the machine is when reloading takes place and the machine must be equipped with a reliable triggering mechanism that is operated by a designated individual. Triggering can only take place prior to launch and after a start order has been issued. In addition to that, the device shall be designed to be easily moved to the launch pad and a layout of the test area shall be clearly stipulated. Material selections, payment for materials, safety regulations such as the inability of the launch to occur in the event the counterweight has been removed, and other rules will have to be adhered to in the design and development process of the project.
Project grading criteria
The project grading criteria are based on a number of rules. These include meeting preliminary design requirements and inbuilt optimality of the system, detailed trebuchet design, and creativity of individual participants (Siano, 5).
Design Considerations
For optimal efficiency, a number of design considerations have to be made. Parametric considerations include dividing the lengths involved in the structure by a constant value, 11(Siano, 5). In addition to that, the masses are divided by a constant value of m 2, and the use of a free sling is another parametric method while continuously varying these parameters and documenting results on a graph. Propping weights in the design to accomplish higher distances has been disputed, but it has been shown to influence the total length of the achieved projection.
Design Process
A problem definition and defining project objectives form the initial step in the design and construction process. Problem identification and description for the typical project are detailed above.
The design process includes identifying moving components of the structure, identifying joints and other parts, modeling the project using computer simulations and other simulation software, performing design simulations, establishing and measuring specific parameters, refining the design by establishing new parameters and sizing them down, and iteratively testing the design parameters against established standards. The final design is optimized to accomplish the best performance of the design.
A new Trebuchet game
One such game includes several others that can be found hosted on different websites. These include where the king has given express orders to an individual to totally destroy his enemies so as to preserve his kingdom. A trebuchet has to be designed to enable the commissioned individual to totally destroy the enemies of the king (Jahed, & Tajik, 3).
Algorithmic beauty of the Trebuchet
The algorithmic beauty of the trebuchet is illustrated in the laws of physics that were exploited at the time of the design. One such expression is in matrix form as illustrated below.
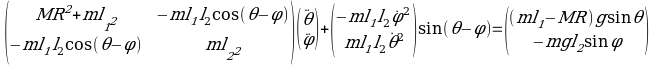
The matrixes expression leads to the equation here defined as,
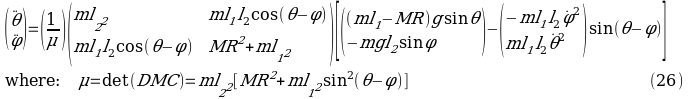
Perhaps it is worth noting that a device with gigantic throwing powers could be developed with time to provide far greater propulsions the future.
Projectile Motion Simulation
The projectile of the trebuchet is discussed as follows. A number of simulations such as the Monte Carlo simulation can be used to simulate the movement of the projectile with air resistance and when there is no air resistance.
Horizontal distance
The Grey Company Trebuchet Page
This page is characterized by a number of pages that contain information about leverage artillery, a number of strange machines commonly referred to as warwolves, and other strange-looking equipment. These machines are historical and detailed information on the design, construction, and operation of the trebuchet machines (Jahed, & Tajik, 65).
The Virtual Trebuchet
The virtual trebuchet can be simulated using a suite of software applications designed to mechanically simulate the trebuchet. Thus, virtual prototypes can be produced using software that dramatically reduces the cost incurred on mechanically physical trebuchets. One of the salient applications used in this industry d the MSC.ADAMS and a family of similar products (Jahed, & Tajik, 2).
Trebuchet Simplified Distance Formula
(X1, y1)
here the following formula defines the mathematical relation of the range efficiency that can be attained by the trebuchet, (Μ/m)(2 v² sin a cos a)/gh = eR = R (2 m1/m2 h where h is the distance descriptive of the fall distance of the counterweight used in the project, and a is the angle of inclination of the horizontal plane to the inclination of the projectile at the time of launch. In addition to that, the distance the counterweight can fall can be analytically obtained as defined in the relation, h = l1(1 – cos (qz)) = l1(1 + sin(yz)).

The geometry of the trebuchet is defined by the horizontal and vertical axes and the forces that act on the projectile. Typically, the origin is pivoted at the beam of the structure, with a specific center of mass indicated by the flow lines (Siano, 5).
Once the trigger has been released from its position it causes the counterweight under the influence of gravity falls. That causes sliding the projectile in the sling along the trough lying horizontally. The accelerating counterweight forces the projectile to cruise from the trough following a projectile motion defined as an arc. Then, o a sling is released in the process allowing the projectile to fly towards the intended target.
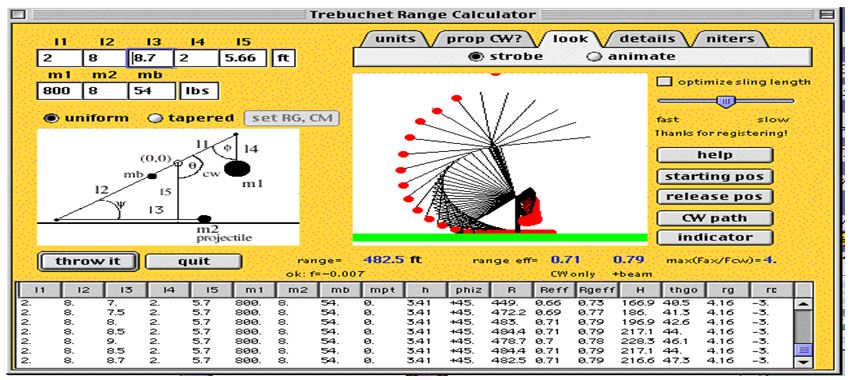
Trebuchet Size Calculator
The calculator consists of an interface where the projectile weight is entered, the counterweight, arm ration, efficiency, required range, and all other detailed information are entered and the required output is generated in real time.
References
Jahed, Hamid. & Arash Tajik. Trebuchet Design. ME380 Project Manual Mechanical Engineering Design Workshop. Department of Mechanical Engineering, University of Waterloo University. University of Waterloo 200 University Ave West Waterloo, ON N2L 3G1, 2006.
Siano, Donald, B. Trebuchet Mechanics. 2001. Web.