Bank A offers to pay you a lump sum of $20,000 after 5 years if you deposit $9,500 with them today. Bank B, on the other hand, says that they will pay you a lump sum of $22,000 after 5 years if you deposit $10,700 with them today. Which offer should you accept, and why?
Solving
The problem here is to determine the bank that will provide the highest value for my money. The value of the money is determined by the rate of return that the bank will offer. Therefore, this question requires that the rate of return that the two banks offer to be determined and the highest rate of the two be used as the basis of determining the bank to choose. Hence, this case will require the application of the future value formula. This assertion holds because the formula entails determining the rate of return being provided by each bank and then choosing the highest of the two. The future value of the two banks is $20,000 and $22,000 for bank A and bank B respectively. On the other hand, the present single cash flow is $9,700 and $10,700 for bank A and bank B respectively. In addition, the period for achieving the targeted amount for both banks is 5 years. Using the following formula, I need to determine the rate of return:
FV= PV (1+r)ⁿ
(1+r)ⁿ = FV/PV
1+r = ⁿ√FV/PV
r = [ⁿ√FV/PV) -1
Where:
- Bank A
- FV= Future value of a single cash flow= $20,000
- PV= Present value of a single cash flow = $9,500
- r= rate of return=?
- n= period of the returns=5 years
Therefore,
r = [⁵√$20,000/$9,500] – 1
I need to determine the ⁵√ of $20,000/$9,500 using an excel worksheet. Here, I will look at the power of this ⁵√$20,000/$9,500, where $20,000/$9,500 is the number and ⁵√ is the power and converted to ¹̷₅

r =1.161 – 1
r =0.161
r =16.1%
FV= Future value of a single cash flow= $22,000
PV= Present value of a single cash flow = $10,700
r= rate of return=?
n= period of the returns=5 years
Therefore,
r = [⁵√$22,000/$10,700] – 1
I need to determine the ⁵√ of $22,000/$10,700 using an excel worksheet. Here, I will look at the power of this ⁵√$22,000/$10,700, where $22,000/$10,700 is the number and ⁵√ is the power and converted to ¹̷₅

r =1.155 – 1
r =0.155
r =15.5%
Decision: The rate of return for bank A is 16.1% while that of bank B is 15.5%. Therefore, I will get a higher return to my money if I invest in bank A. In an absolute term, it would seem worthwhile to invest in bank B since an extra profit of $2,000 ($22,000 – $20,000) will be made. However, one will have to invest an extra amount of $1,200 ($10,700 – $9,500). Prudently, I will invest $9,500 in bank A and then look for another investment that can raise a higher return than 15.5% to invest the extra amount of $1,200 or even invest in Bank B. This move will fetch me some extra returns.
Case 2: You have decided that you will sell off your house, which is currently valued at $300,000, at point when it appreciates in value to $450,000. If houses are appreciating at an average annual rate of 4.5% in your neighborhood, for approximately how long will you be staying in the house?
Similar to the first case, this case will utilize the future value formula to determine the period that I will stay in the house until it appreciates to a value of $450,000 for me to sell it. Therefore, the future value of the house is equivalent to $450,000. The current value of the house of $300,000 will be used as the present value. The rate of return in this case is equal to 4.5%, but I will have to determine the period of the appreciation to the target figure as follows:
FV= PV (1+r)ⁿ
(1+r)ⁿ = FV/PV
1+r = ⁿ√FV/PV
n = {[ln(FV/PV)]/[ln(1+r)]}
Where;
- FV= Future value of a single cash flow= $450,000
- PV= Present value of a single cash flow = $300,000
- r= rate of return=4.5% or.045
- ln= returns the nature logarithm of number
- n= period of the returns=? Years
Therefore;
n = {[ln($450,000/$300,000)]/[ln(1+ 0.045)]}
n = {[ln1.5]/[ln1.045]}
Finding the natural logarithm (ln) of 1.5 and 1.045, and n using excel worksheet
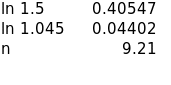
n = 0.40547/0.04402
n = 9.21 Years
Decision: The time required to lapse until the house appreciates to $450,000 is 9.21 years. Therefore, I will sell the house after 9.21 years since it will have appreciated to $450,000.