Introduction
The term Traveling Salesman Problem (TSP) refers to the difficulties associated with determining the path that is both the quickest and most cost-effective for a single person to take when traveling to a series of predetermined locations. The traveling salesman problem is an algorithmic problem that aims to discover the shortest route between a collection of locations and points that need to be visited.
When examining the supply chain, the ‘places’ that need to be visited are the various cities and towns (Cacchiani et al., 2020). During sales operations, a salesperson’s primary mission and priority are to reduce unnecessary travel time and expenses as much as possible. People have access to a wide variety of pathways, but it is the primary goal of computer scientists and mathematicians to identify the one that provides the most significant benefit.
The Traveling Salesperson problem has been utilized to locate the most expedient method for a traveling salesperson to arrange specific locations they are required to visit before returning home. On an occasion where one or more people desire to travel to a location most quickly and least expensively possible. In that case, the TSP can be utilized virtually every facet of daily life.
Within the context of the supply chain, TSP contributes to determining the ideal geographic route that salespeople may take to visit specified sites and then return to the starting point, all while minimizing the amount of time spent driving and the amount of money spent on gas. It is always difficult for delivery agents responsible for the last mile to discover the quickest path to get products to customers while spending the least time and money on travel (Di Pretoro et al., 2021).
TSP is now a complicated problem made worse by the endless delivery-based constraints, such as traffic inspections and congestion. The traveling salesman problem is one of the most challenging platforms to assess algorithms’ performance. This is because of the intricacies that are involved in solving the problem. For example, there are 181,440 routing possibilities between just ten locations.
Companies utilize two essential factors to achieve commercial success and set themselves apart from their contemporaries. They are more concerned with maximizing the delight of their customers and expanding their surplus than with the return on their investments. When factors such as customer happiness and the supply chain’s effectiveness are considered, operations scheduling algorithms such as the traveling salesman issue to contribute to an organization’s value proposition.
TSP can increase the supply chain’s effectiveness by reformulating logistical processes that accelerate product delivery to customers. The idea of meeting and exceeding the expectations of one’s customers helps contribute to eight different logistical rights. The “right way” is one of the rights, and it maximizes the effectiveness of the route traveled to reduce the amount of money and time spent on transport and company activities.
Model
There is a varied range of models that might help analyze and find solutions to TPS issues. On the other hand, a model selection is contingent on a hypothetical viewpoint that is network- and representation-specific. In the logistics model, operations managers often consider locations and destinations network nodes or edges that comprise a transportation network (Sahana, 2019).
If a company’s logistics covers particular nodes in a given geographical region, then those particular nodes are places that salespeople are required to visit. Modern navigation technology can be considered one of the models that can be utilized to generate a solution for the best potential path to reach all destinations at the minor cost and distance achievable (computer simulation model).
Current navigation knowledge can handle transportation tasks by casting them as integer problems and then applying linear programming to those problems. This must be done under certain methodological constraints. In addition, the model uses apparent linkages to find solutions to specific issues that arise during the production and distribution planning processes (Zakharov et al., 2017).
For illustration’s sake, the decision variable that connects the nodes of the network XIJ, where both I and J can take on just two values. In the event that the proposed route IJ does not receive authorization from the relevant transportation authorities, the CIJ equation can be rewritten so that the XIJ variable always equals zero. Therefore, the traveling salesman issue can be expressed as a function of the form Z = ∑I ∑J XIJ*CIJ, where I denotes the integers 1, 2, and 3… The Nth value and ∑I XIJ have the same value, which is one.
∑J XIJ equals one when J = 1, 2, 3…Nth value
XI1, J1 + XI2, J2 + XI3, J3…+ XIN, JN = N
In the function, J1 = I2, J2 = I3, J3 = I4…JN = I (N + 1)
As a result, one can express the model for the Traveling Salesman Problem as shown below.
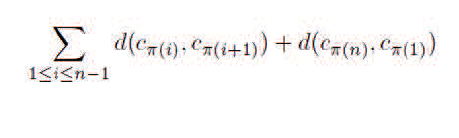
This constraint organizes the required routes to make a single stop at each destination. The following methods can create a closed circuit that begins and ends at the same spot. The routes are represented by the edges, while the nodes represent the places or destinations (Cacchiani et al., 2020). It is essential to remember that the length of the arrows does not correspond to the distance. Simply enough, the distance matrix was not drawn to scale when it was created.
Many different ways can be utilized to resolve problems associated with transport salespeople; however, the amount to which those methods are useful depends on the efficiency of the models’ processes. Models include the computer simulation model, the entire listing method, the branching and bound method, the efficient algorithm developed by Clarke and Wright, the genetic algorithm, and the ant colony optimization algorithm (ACO).
Other models include the effective algorithm established by Clarke and Wright and the generic algorithm (Zakharov et al., 2017). Because it enables the production of simulation models and contributes to the growing power of programs, the computer simulation criteria have become the TPS model that is most frequently utilized. The simulation power of such a tool helps resolve difficult traveling salesperson problem values. The fact that the computer simulation model can accept random computer sampling on a vast scale is one of the advantages of using that model.
Solving an Example
To demonstrate that TSP is applicable in practice, the following scenario can be used
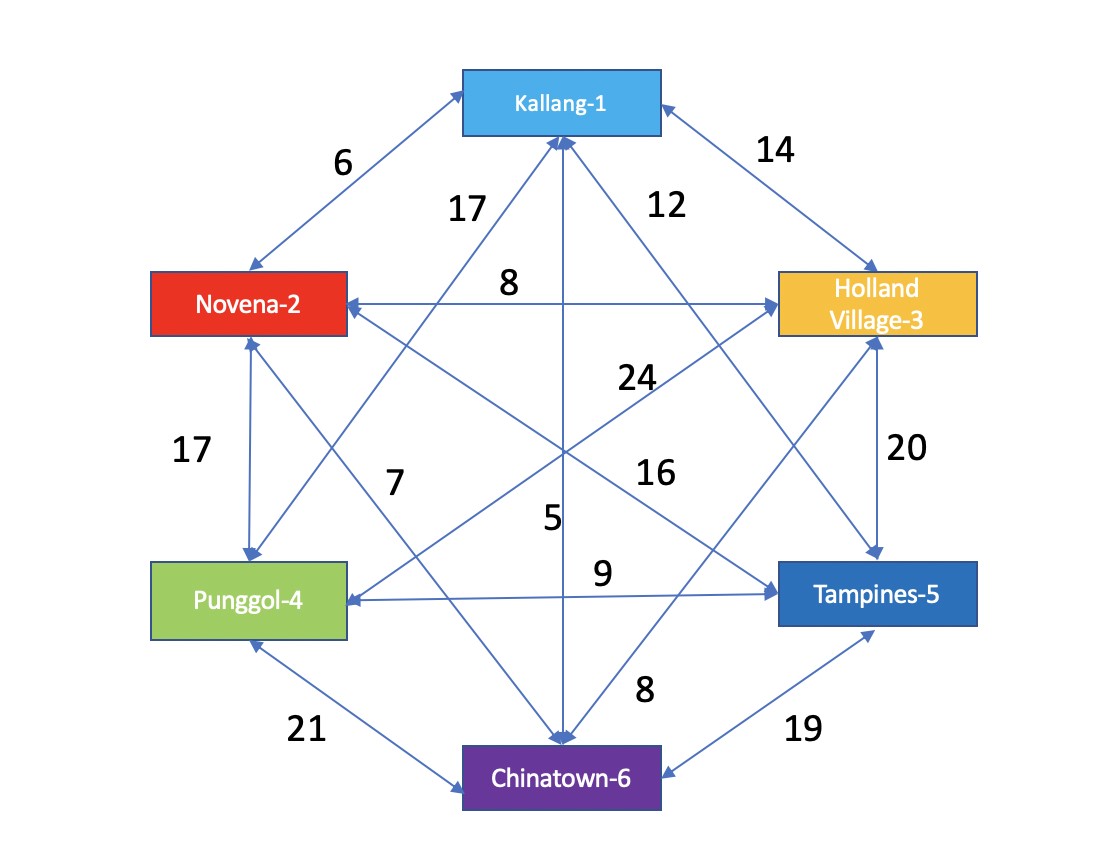
The figure shows a network design to deliver all customer orders to all five stores before returning to the main distribution center in Kallang as efficiently as possible. The first node is both the beginning and the end. Objective function selection is a mathematical model that can assist in reducing the amount of distance that must be traveled in traveling salesperson difficulties.
An objective function determines whether or not an optimization procedure is successful when solving the traveling salesman dilemma (Zakharov et al., 2017). When defining an objective function, selecting a target allows one to choose either a single design response or a group of design answers. For example, in a traveling salesman problem, the target may be to minimize the number of miles traveled.
Use of Solver Equation
Using the solver equation, which functions according to the idea of the generic algorithm, it is straightforward to find the route that will result in the best possible outcome. According to the table that can be found below, there are many different ways to get to the locations that are being shown. The selection of the objective function, on the other hand, is what determines the optimal route by looking at the shortest outcomes in the shortest route. This means that the optimal model depends on the objective function selection. For instance, the method that takes up a considerable amount of time is 857 minutes. As a result, it can be determined that optimizing time for 756 minutes is the quickest duration, yet this results in the most time-consuming route.
Raw Minimization
The lowest possible score in the first row is a 4.
Row Minimization
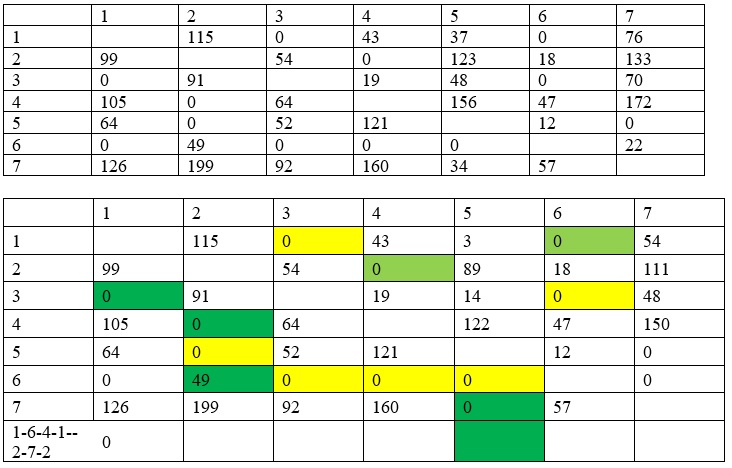
Findings and Interpretation
A salesman is only allowed to use 558 minutes at the very minimum. As a result, the most efficient path takes 558 minutes. Therefore, the solution for getting from town 1 to town 7 is found in the most efficient route. A programming language that uses mathematical modeling can be used to check whether or not the findings are accurate in this instance.
Literature Review on the Application of Travelling Salesman Problem in Supply Chain Design and Analysis
Problems in the Supply Chain Addressed by the Travelling Salesman Problem
The TSP is one of the optimization methods used most frequently in supply management chains and logistics. The sequence of picking an issue in warehouses, planning routes, and cutting circuit boards are the three most common challenges in the supply chain that TSP could handle. TSP’s primary value addresses the problem associated with warehouse order picking. Customers’ desired stock-keeping units (SKUs) are gathered during the order-picking process (Yakoob, 2017). When a consumer orders a specific number of things stored in a warehouse, the vehicle will get them all to ship them out. In this way, the TSP connection is made official.
The stock-keeping units (SKUs) must be kept within easy reach, so the warehouse must be laid out to facilitate efficient picking and vehicle routing. The SKUs are often kept in the longitudinal picking aisle of modern warehouses, which is part of a conventional multi-parallel aisle layout. Similarly to how nodes in TSP represent storage locations, the time it takes to travel between two storage locations is a measure of their relative distance. As a result, the computer could calculate the fastest path for the car to pick up the fewest people.
The planning of routes is another issue that arises in the supply chain and might be resolved with the help of TSP. The goal of route planning is to reduce the overall distance covered by transportation by determining the most efficient path for delivering goods (Baniasadi et al., 2020). However, many other factors, such as time and capacity limitations, need to be considered in real-world scenarios, making the problem difficult to address. As a result, heuristics algorithms are typically the ones that are utilized to solve problems of this nature since they can tackle problems involving a moderate to the high number of nodes.
Similarities
Both ‘The Travelling Salesman Problem and its Application in Logistic Practice’ (Filip and Otakar, 2011) and ‘The Travelling Salesman Problem: History of TSP Computation (Scholz, 2019) (Chapter 4)’ asserted that they do not suggest solving TSP by using the Branch and Bound method as it is too labor intensive to solve a large number of nodes. These chapters can be found in ‘The Travelling Salesman Problem: History of TSP Computation (Baniasadi et al., 2020)’
The procedure does not always ensure that the initial trial will result in the best possible solution. This approach can only solve optimally small nodes with a size of fewer than 100. In addition, the lower limit numbers produced by the linear programming relaxation (LP relaxation) are inconsistent, which is another factor that contributes to the possibility that the first solution is not the optimal one.
The articles ‘Solving Traveling Salesman Problem Using Genetic Algorithm’ (Saloni and Poonam, 2013) and ‘A Comparative Study of the Nearest Neighbor and Genetic Algorithms: A revisit to the Travelling Salesman Problem’ (AlSalibi et al., 2013) indicated that genetic algorithm is a common method for solving the TSP. An evolutionary algorithm used to tackle complicated problems is known as a genetic algorithm (Saloni and Poonam, 2013).
Finding all possible answers and then optimizing that solution through a process of crossover and mutation are both parts of the process. The genetic algorithm is a quick method that can produce optimal results and performs significantly better than its Nearest Neighbor counterpart. The term “nearest neighbor” refers to a statistical technique that compares the distribution of distances between a data point and its nearest neighbor with a data set that has been randomly dispersed.
Differences
Two articles, ‘Solving the TSP with Traditional Computing’ (Baidoo and Oppong, 2016) and ‘A restriected dynamic programming heuristic approach for the time-dependent traveling salesman problem’ (Malandraki and Dial, 1996), suggest that dynamic programming and the greedy method are related but distinct. These two approaches use an ideal substructure, where the optimal solution incorporates the best answers to the problem’s constituent sub-problems.
On the other hand, dynamic programming is a type of exact algorithm whose solutions are guaranteed optimal. In contrast, the greedy approach is a heuristic that always finds the best possible compromise when the TSP cannot be solved exactly. Dynamic programming is intended to identify the optimal solution; therefore, it will search exhaustively through all the sub-problems and pick the best one, while the greedy method searches through a single one.
Suitability of Using the TSP in Design/Analysis of Various Supply Chains
The ideal solutions to the traveling salesman problem, which minimize travel time and costs, can be easily calculated by computer. As a result of its complexity, TSP has become one of the most advanced environments for evaluating the efficacy of any given algorithm (Yakoob 2017). The company must determine the most efficient path to take to acquire resources from a wide variety of vendors and then deliver those resources to the right clients at the right time, all while keeping in mind the need to minimize cycle and purchasing expenses and travel time. However, most products require suitable packaging to facilitate easy transit, storage, and distribution.
Due to the hazards and laws involved, transporting incompatible or dangerous commodities in the same vehicle, such as food and chemicals, may be hard. There is a possibility that the TSP routes will be condensed from several to just two or three stops. Accident and incident risks could be drastically minimized and better managed with this limitation.
Limitations of TSP
As was indicated previously, TSP is computationally challenging, and hence, the application is limited to effectively tackling only minor problems. Solving a reasonable TSP size will need to take a significant computing period. In real-world circumstances, there are numerous enormous size difficulties which it can get complicated and longer to discover a clear solution. This implies that the number of viable solutions grows exponentially with the number of inputs (nodes). Consequently, the method can only provide the best possible solution within an acceptable computational period, not a guaranteed optimal solution.
Additional Critical and Content Analysis on the Application of TSP in the Design and Analysis of Supply Chain
There are many different approaches to solving TSP, which makes it an NP-hard problem. Although it is challenging, they can ensure optimality by employing various methods. When it comes to the effectiveness and efficiency of a supply chain, it all comes down to the planning and timing of the operations involved.
Computer science and operational research study operations scheduling as an optimization problem. In operations scheduling, where multiple jobs need to be completed in a limited time, the TSP is used to achieve this goal. As a result, both consumer happiness and supply chain effectiveness are improved thanks to the solution. Yakoob (2017) states that FedEx, DHL, and UPS, the three largest logistics businesses, use TSP models to improve their scheduling operations using an iterative method. As a result, corporations have dramatically reduced their labor, operating, and transportation costs.
Conclusion
In conclusion, the supply chain analysis and design have advantages and disadvantages regarding the traveling salesman dilemma. In contrast to other algorithms, TSP produces solutions that are not susceptible to failure, which can be categorized as a strength or advantage. Another advantage of TPS is that it helps in the optimal positioning of facilities, which reduces the amount spent on transportation costs and improves the effectiveness of the supply chain network.
On the other side, one of the drawbacks of the traveling salesman problem is that it cannot fulfill the requirements of all partners in a horizontal logistics coalition. This is one of the problem’s limitations. Another shortcoming of the algorithm is that it does not contribute to resolving even the most basic or sophisticated supply chain problems.
TSP has the potential to solve many supply chain issues. Several real-world methods are founded on TSP, and several algorithms have been created to address it. To ensure the solution is practical and effective in use, it is also important to consider the circumstances and requirements of the problem. Therefore, to ensure optimality, each problem must select an appropriate TSP model for the solution. TSP can help businesses in numerous ways, including reducing their carbon footprint, working more efficiently, and saving money.
Reference List
AlSalibi, B.A., Jelodar, M.B. and Venkat, I. (2013) ‘A comparative study between the nearest neighbor and genetic algorithms: A revisit to the traveling salesman problem.’ International Journal of Computer Science and Electronics Engineering (IJCSEE), 1(1), pp.110-123.
Baidoo, E. and Oppong, S. (2016) ‘Solving the TSP using traditional computing approach.’ International Journal of Computer Applications, 152, 13-19.
Baniasadi, P., Foumani, M., Smith-Miles, K. and Ejov, V. (2020) ‘A transformation technique for the clustered generalized traveling salesman problem with applications to logistics.’ European Journal of Operational Research, 285(2), pp.444-457.
Cacchiani, V., Contreras-Bolton, C. and Toth, P. (2020) ‘Models and algorithms for the Traveling Salesman Problem with time-dependent service times’. European Journal of Operational Research, 283(3), pp.825-843.
Di Pretoro, A., Negny, S. and Montastruc, L. (2021) Flexibility analysis in supply chain management: application to the Traveling Salesman Problem. In Computer aided chemical engineering (Vol. 50, pp. 1721-1726). Elsevier.
Filip, E. and Otakar, M. (2011) ‘The travelling salesman problem and its application in logistic practice.’ WSEAS Transactions on Business and Economics, 8(4), pp.163-173.
Malandraki, C. and Dial, R. B. (1996) ‘A restricted dynamic programming heuristic algorithm for the time-dependent traveling salesman problem’. European Journal of Operational Research, 90(1), pp. 45–55
Sahana, S.K. (2019) ‘Hybrid optimizer for the traveling salesman problem’. Evolutionary Intelligence, 12(2), pp.179-188.
Saloni, G. and Poonam, P. (2013) ‘Solving Travelling Salesman Problem using genetic algorithm.’ International Journal of Advanced Research in Computer Science and Software Engineering, 3, 376-380.
Scholz, J. (2019) ‘Genetic algorithms and the traveling salesman problem a historical review.’ arXiv preprint arXiv:1901.05737.
Yakoob, S.H. (2017) Travelling Salesman Problem & the 8 “RIGHTS” Of Logistics. SCMDOJO.
Zakharov, O.V., Balaev, A.F. and Kochetkov, A.V. (2017) ‘Modeling optimal path of the touch sensor of coordinate measuring machine based on traveling salesman problem solution.’ Procedia Engineering, 206, pp.1458-1463.