Executive Summary
The problem of long waiting lines is an issue of major concern to many companies operating in various sectors. Vodafone, a global telecommunications company, faces this problem, especially in relation to the provision of customer care services. The following report proposes a solution for the long waiting periods witnessed at Vodafone’s Berkshire branch. The problem arises when the customers experience a prolonged delay before they can access services.
The report proposes a multichannel single phase waiting line model as a way of resolving the problem. The model is enhanced by a mathematical formula, which can be used to manipulate the various elements in it. The proposed waiting line model and mathematical formula can be effectively used to reduce or eliminate the problem experienced at Vodafone’s Berkshire branch.
Vodafone Telecommunications Company
Vodafone is one of the leading global telecommunications companies in the world. It provides a wide range of services in the mobile communications industry. The company operates in more than 30 countries worldwide. It has entered into partnership with more than forty networks in different parts of the world (Vodafone Limited, 2014). The company has a customer base of approximately 360 million subscribers. The employees working for the organisation are more than 8000 (Vodafone Limited, 2014). The company has made significant investments in the industry. It is associated with innovativeness and the provision of award-winning customer care services.
Some of the products offered by Vodafone include mobile phones and telecommunications coverage (Vodafone Limited, 2014). In addition, the organisation hosts online shops from where customers can purchase these products. Consequently, many customers make calls to Vodafone service centres seeking some form of assistance or making enquiries about various products.
Problem
The problem of clients waiting in long queues arises either due to jammed traffic or as a result of inadequate customer care service assistants. As a telecommunications company, Vodafone faces challenges associated with these long queues in its networks. The management understands that rises in the volume of calls made to the customer care centres may take place any time.
Staffing to cater for anticipated seasonal changes proves difficult for the company. To make matters worse, unpredictable rises in the volume of customers may damage the reputation of the global organisation. The erratic changes may result from such factors as the introduction of new products and power outages. Severe weather conditions and staff shortage may also lead to increased call volumes and waiting time. Consequently, these factors impact on the ability of Vodafone to satisfy the needs of the callers. They also affect the company’s goal of effective cost management.
The current report addresses the problem of customers waiting in long queues either to buy products or to get services in one of Vodafone’s stores. The store is called Vodafone House and is located in Newbury Parish in the county of Berkshire, England. Improvements made in information communication technologies have eased the queuing problem to some extent. However, a lot needs to be done to eliminate or reduce the problem.
Scope of the Report
The report explores some of the various techniques used in addressing long waiting queues in different industries. Queuing theory and waiting line models are explored in relation to Vodafone’s Berkshire branch. The theory and the model are analysed with regards to their applicability in the telecommunications industry. To this end, their viability in Vodafone Company is reviewed.
There are various approaches that can be adopted to address the issue of long waiting lines in the telecommunications sector and other industries. One of them is the mathematical model, which is proposed in this report.
Definition of Concepts
Queuing System Defined
According to Gross and Harris (1974), the queuing system is made up of three major components. The first component includes the source population. In the context of this report, the element refers to the customers making calls to Vodafone service centre. The second component is service system. The system refers to call lines and customer service. The third element consists of customers who are exiting the system.
The queuing system at Vodafone’s Berkshire branch consists primarily of the waiting lines and the number of servers used to attend to the callers. As such, addressing the problem of the long lines begins with the analysis of the company’s queuing system.
Queuing Theory and the Waiting Line Problem
According to Kleinrock and Gail (1996), a waiting line problem arises under two conditions. The first is when clients are made to wait before their issues are dealt with. The delay can be brought about by a shortage in servicing facilities. In Vodafone, the problem arises when customers ‘overwhelm’ the servicing facilities (servers and operators) through increased call traffic.
The second condition leading to waiting line problems is realised when servicing facilities remain idle (Prabhu, 1997). Idle time can result from a low number of customers. It can also result from the nature of time spacing between customer arrival and the duration they have to wait before they are served (Prabhu, 1997). Both conditions mentioned above lead to a waiting line. In the first scenario, the queue is made up of clients waiting to be served. In the second case, the waiting line is brought about by facilities or personnel waiting to serve the customers. In Vodafone, the first condition is more apparent than the second one. Customer calls are put on hold as they wait to be served.
The waiting line problem involves altering the behaviour of arriving units, the service facilities, or both (Kleinrock & Gail, 1996). Effecting these changes requires the manipulation or control of such factors as order of service, arrival rates, and number of service facilities (Prabhu, 1997). The logic behind the manipulation of these elements involves striking a balance between the pertinent features entering the process in an efficient and economical manner.
Application of the waiting-line theory and the formulation of solutions for the problem rely on such features as the average length of waiting line and the standard time spent in the queue. Other features influencing the measure include the average service rate and the standard arrival rate. All the factors constitute the functions of input and output.
Queuing System Designs
There exists various queuing system designs that Vodafone can adopt to reduce the problem associated with long waiting lines. According to Render, Stair, and Hanna (2012), service systems are categorised based on the number of channels or servers. In addition, the number of phases that customers go through before they are served is considered when classifying system designs. Queuing system designs are also referred to as line structures.
The line structure constitutes the basic step in addressing the challenges that come with long waiting lines. The selection of a particular queuing system is informed by a number of factors. To some extent, the choice depends on the volume of customers to be served and the restrictions arising from sequential requirements. The requirements govern the order followed in providing services.
The queuing system design can take different forms. It can be single channel or single phase. In this case, customers access all the services they require from one service centre (Kleinrock & Gail, 1996). The other category is single channel multiphase system. Here, the clients are served from one access point (Prabhu, 1997). Multichannel single phase design involves numerous servers. Each of these servers is used to provide the customer with all the services they require (Prabhu, 1997).
Other designs include multichannel multiphase and mixed system. The former involves numerous servers that serve customers in stages (Prabhu, 1997). The second design combines a number of the other line structures to suit the needs of a particular organisation.
The various queuing design systems or line structures can be depicted as follows:
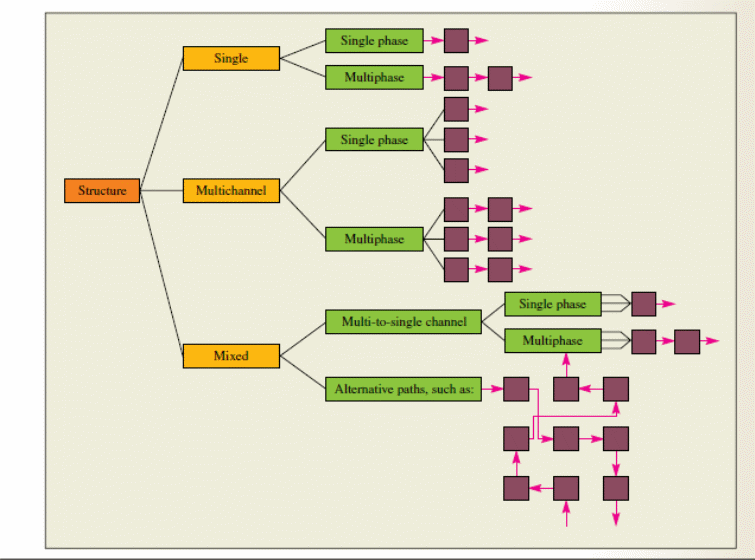
In light of these queuing line structures, management at Vodafone Berkshire requires to select the most appropriate model that will address the unique queuing problem of the company. The table below shows some of the common waiting line models that the company can choose from:
Table 1: Properties of specific waiting line models. Source: Prabhu (1997).
Proposed Solution to the Long Waiting Queues at Vodafone Berkshire
Proposed Queuing Model
Multi-channel single phase system is the model proposed to resolve the queuing problem at Vodafone Berkshire (see figure 2 below). The basic components of any queuing process include the rate of arrival, time taken to serve the customer, and the queue itself (Kleinrock & Gail, 1996). In the proposed model, the service rate is not tied to any specific distribution. However, the arrival rate assumes the Poisson distribution system (Render et al., 2012).
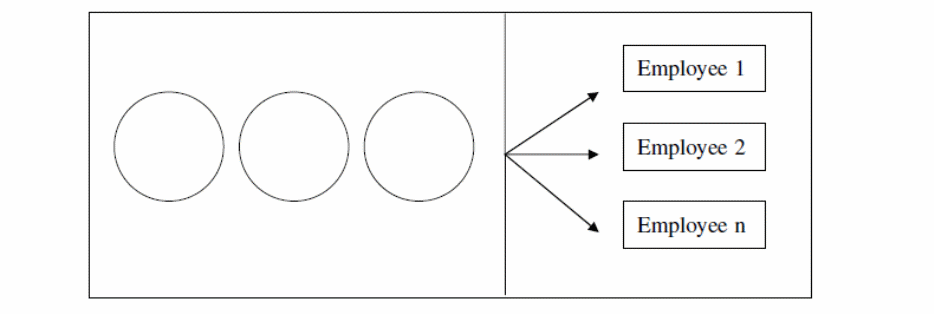
Factors Influencing the Queuing Problem at Vodafone Berkshire
The various attributes of the customer service centre determine the nature of the waiting line problem experienced by the company. The element of customer service at this branch justifies the queuing model proposed. The factors affecting the waiting problem include the queuing environment at the centre, which exhibits infinite calling population. In addition, the customer service centre has multiple channel facilities.
The other factor is rate of arrival as far as calls at the centre are concerned. The calls are largely unpredictable. The erratic nature can be described through Poisson distribution, which supports the proposed model (Brown et al., 2005; Whitt, 2005). Service time, which refers to the rate at which calls are processed at the service facility, exhibits exponential distribution. It is also unpredictable.
Other factors include the waiting time for calls made to the centre. The time is infinite and all the customers wait on a single queue. Clients who access the centre are served on a first-come first-served basis. All arriving events join the queue. None of them is prioritised (Hillier & Yu, 1981).
The Operating Method of the Proposed Queuing Model
The proposed model minimises and eliminates waiting with regards to arriving events. The method supports multiple service channels. When customers contact Vodafone Berkshire, the calls arrive at an average rate of λ. They follow Poisson’s probability distribution (Render et al., 2012).
On the other hand, service calls are different. They assume an average rate of μ calls per minute for each and every channel. Consequently, the arriving calls seek to be served from any of the service channels. Alternatively, each and every call is switched automatically to the open server. In the case where all channels are busy, the arriving calls may be denied access to the system. Since there is no ideal man-made system, calls that arrive when the system is blocked or full are cleared and considered as abandoned (Render et al., 2012).
According to Render et al. (2012), the following formula can be used to calculate the probability of the channels being busy:
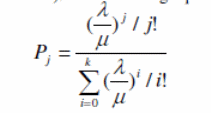
Where:
- λ= the mean arrival rate.
- µ= the mean service rate for each channel.
- k = the number of channels.
- Pj= the probability that j of the k channels are busy for j = 1, 2,…,k.
Charnes, Cooper, Lewin, and Seiford (1995) advance the following formula in relation to the one above:
L =l/μ (1-Pk).
Where L= average number of events within the system.
Pk shows the probability that all channels are busy. On a percentage basis, the element indicates arriving calls that are blocked and abandoned (Charnes et al., 1995). In addition, the component indicates the average number of events in the system. The events are the same as the average number of channels being used (Render et al., 2012).
The two formulae above can be used to calculate the quantity of channels or servers that can be used to handle a given number of calls. The number of incoming calls at Vodafone Berkshire can be estimated. As a result, the management can provide the correct number of servers based on the proposed model. The service rate in the model can be computed using the formulae and adjustments made to facilitate efficient service delivery. Ultimately, the problem of long waiting lines at the centre can be minimised or eliminated.
The model proposed for Vodafone Telecommunications Company’s Berkshire branch is referred to as the mathematical approach. The proposed equations can be manipulated to address the various elements of the process. The findings made can be integrated into the physical facilities.
Economics of the Waiting Line Problem
The main challenge associate with any waiting line revolves around making trade-off decisions (Bard & Bejjani, 1991). The management has to take into consideration the added cost involved in the provision of improved services. The decisions involve the acquisition of additional communication facilities. The costs involved are weighed against the inherent expense of the clients waiting in the line. In most cases, the cost-trade off decision is straight forward.
In the case of Vodafone Berkshire, the costs incurred by customers when they hold calls as they wait to be served can be mitigated by using more channels. The costs can be defined in terms of dissatisfaction, forcing the clients to go to the competitors (Davis & Maggard, 1990). Vodafone can acquire more channels and servers, satisfying and retaining the customers in the process.
Figure 3 below illustrates the trade-off relationship that results from typical conditions of customer traffic:
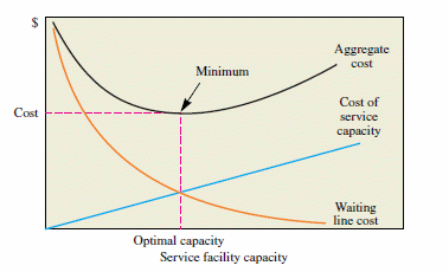
When the service capacity is minimised, the costs associated with waiting line are maximised. Increasing the service capacity has the opposite effect. It reduces the number of clients that are kept waiting. It also reduces the time it takes to serve them. The overall effect is a decrease in waiting line costs (Davis & Maggard, 1990). The negative exponential curve represents variations in this function. The ideal optimum cost is achieved at the crossover point between the waiting and service capacity lines.
An analysis of figure 3 makes it apparent that the cost of services increases when firms try to raise their capacity. Managers at Vodafone Berkshire can vary the firm’s capacity by maintaining ‘standby’ personnel or other service facilities (Whitt, 2005). The standby channels and servers can be assigned to specific facilities.
Conclusion
The long waiting lines at Vodafone Berkshire are a major issue affecting both the company and its customers. Failure to address this problem can result losses for the organisation. For example, Vodafone may lose the customers to competitors. Clients develop loyalty based on how well they are handled. The proposed multichannel single phase system queuing model provides the ultimate line structure that can used to effectively serve the customers calling Vodafone Berkshire. The model, together with the mathematical approach, allows for the manipulation of various elements in the system.
Developments in communication technology can provide efficient solutions to the waiting line problem. As such, Vodafone should embrace these technologies to strengthen its position in the market. In the meantime, the system proposed in this report can be used to solve the waiting line problem.
References
Bard, J., & Bejjani, W. (1991). Designing telecommunications networks for the reseller market. Management Science, 37(9), 1125-1146. Web.
Brown, L., Gans, N., Mandelbaum, A., Sakov, A., Shen, H., Zeltyn, S., & Zhao, L. (2005). Statistical analysis of a telephone call centre: A queuing science perspective. Journal of the American Statistical Association, 100, 36-50. Web.
Charnes, A., Cooper, W., Lewin, A., & Seiford, L. (1995). Data envelopment analysis: Theory, methodology, and applications. Dordecht, Netherlands: Kluwer Academic Publishers. Web.
Davis, M., & Maggard, M. (1990). An analysis of customer satisfaction with waiting times in a two-stage service process. Journal of Operations Management, 9(3), 324-334. Web.
Gross, D., & Harris, C. (1974). Fundamentals of queuing theory. New York: Wiley. Web.
Hillier, F., & Yu, O. (1981). Queuing tables and graphs. New York: Elsevier Science Ltd. Web.
Kleinrock, L., & Gail, R. (1996). Queuing systems: Problems and solutions. New York: Wiley. Web.
Prabhu, N. (1997). Foundations of queuing theory. Dordecht, Netherlands: Kluwer Academic Publishers. Web.
Render, B., Stair, R., & Hanna, M. (2012). Quantitative analysis for management (11th ed.). Upper Saddle River, NJ: Pearson/Prentice Hall. Web.
Vodafone Limited. (2014). Our company. Web.
Whitt, W. (2005). Engineering solution of a basic call-centre model. Management Science, 51(2), 221-235. Web.