Statistics Abuse: How, Why, and When Report

Executive Summary

This report presents a number of notable abuses of statistics. Literature research on the topic has revealed that the abuses of statistics can occur during sample collection or during evaluation of the collected sample. Some of the contributing factors include bad or small sample, misleading graphs/charts, misleading percentages, incomplete data, guess estimates, loaded questions, partial pictures as well as correlation and causality.

Abuse results when inference is made without regard to some of these factors. This can be due to deliberate attempt to produce deceiving results or application of a wrong methodology. In this report each of the mentioned abuses are explained. The explanations are supported with relevant examples. At the end of the report recommendations for avoiding such malpractices are suggested.

Introduction

The foundation of modern statistical inference was laid in the late 20^th century, with the field having its roots in classical mathematics. In a relatively short period of time, statistics has undergone immense growth to become a multidisciplinary subject. This is evidenced by the high number of disciplines it has become incorporated in such as social sciences, chemistry, ecology, geology as well as finance ,to mention just but a few. A number of completely novel subjects have also spurned of from statistics. These include econometrics, chemometrics and environmetrics.

Basically, statistics involves mathematically evaluating a sample and drawing a plausible conclusion about its population. The conclusions gathered are used to build the knowledge base for the related disciplines. In business enterprises statistical results are crucial for decision making.

For accuracy, the sample collection and analysis should be carried out cautiously and interpretation made without any bias. However, in some cases, the inference is skewed or is entirely incorrect. The inaccuracy may be due to unintentional methodological and computational errors or as a result of deliberate manipulation to deceive about perception and ideas of a particular subject. The later is what constitute an abuse of statistics.

This report is as a result of a literature research conducted on how, why and when statistics can be abused. It explains using appropriate examples ways in which statistics is abused and offers suggestions on how to avoid such errors as well as how to identify flawed statistical inference

Specific abuses of statistics

Case study: Abuses of statistics in geology

Kriged variance and covariance

Kriged variance and covariance are some of the widely applied computations in geostatistics. In a marked deviation from classical mathematical statistics they are based on, they do not fully observe degrees of freedom for a dataset. Proponents of geostatistics continue to disregard the degrees of freedom (d (f) (r or o)). However, a set of n independently measured values has been found to have df(r) = n-1, while that for a temporary set is df (o) =2(n-1).

Variance for a randomly distributed and ordered datasets in single or more samples spaces are commonly used in exploration, mining and metallurgy. According to the formula of variance for any randomly distributed set of data, the denominator denotes the degrees of freedom:

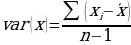
Where,

• var[x] – variance for a random set;
• ^‘x – mean for the set of data;
• x_i – i^th datum;
• n – no. of data in the set;
• n – 1 – degree of freedom for the set.

Kringed estimate for a set of measured independent data uses a kriged variance and a set of arbitrary data based on an assumed spatial dependence. This makes it invalid because it fails to measure up to the requirement of statistical independence.

Another common abuse of statistics is found where differences between a pair of statistically identical variances are entered into smoothing relationship to predict tonnages and grades of ores. This aberration has been corroborated by Amstrong and Champigny who found that for a variogram range less than half the sample size spacing, the Kriged block estimates were found to be uncorrelated with actual grades. Kriged estimates were derived from distance weighted averages. However because this estimates do not rely on any degree of freedom, it becomes impossible to test for their statistical significance or insignificance.

Abuse in central values

In mathematical statistics, central values such as arithmetic means of sets of measured values with equal weights or area-, count-, density-, distance-, length, mass- , and volume-weighted averages of sets of measured values with variable weights do have variances. The variance of each of the values is derived from the formula of variance of a set of data:

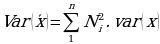
Where,

• var[x] – Variance of set;
• N² – Squared i^th weighting factor. It can also be shown that the central limit theorem is given by var[^‘x] = var[x].

The Central Limit Theorem defines the relationship between the variance of a set of n measured values with equal weights and the variance of its arithmetic mean. All variances converge on the Central Limit Theorem as variable weights converge on the same constant weight.

In geostatistics the weighted average is defined by the central value of a set of measured values with variable weights. From mathematical statistics, this implies that each of the weighted average- area, count, density, distance, mass, and volume does have some variance. For yet to be explained reasons, not all weighted averages used in geostatistics have variances.

Nowhere is it explained how and when the variances were done away with. This is especially the case for distance-weighted average and length-weighted averages. Furthermore, the variance-deficient distance-weighted average and length- weighted averages were reworked unconvincingly to end up with Kriged estimates or Kriged estimators. The variance of Kriged estimate is defined as:

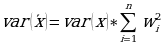
Where,

• var[^‘x] – variance of Kriged estimate;
• var[x] – variance of randomized set;
• w² – First variance term of ordered set;
• n – number of measured values.

A Kriged estimate’s variance is derived from the probability theory and is a dependent variable of a set if independently measured values of a random variable determined at different coordinates in a sample space. The striking difference between this estimate and classical statistics is that it lacks variances that must be there to fulfill the distance-weighted average for an infinite set.

Non-specific abuses of statistics

Bad samples

Bad sample selection leads to a biased inference. An example may be a survey asking workers of factory about their views on a particular product they manufacture. In such a case, the workers may feel obliged to give positive responses just for the sake of the survey although they may be having totally different opinions about the same.

Small samples

Due to resource constraints, a research group may be forced to select small samples from the target population. Large samples are expensive and can only be carried out by governments and well funded organizations. Problem arises when the results of a small sample study are inferred to reflect the general population. If the sample size is small, it is likely the results will be highly influenced by extreme values especially for highly skewed distributions.

Misleading graphs/charts

Graphs are one of the common ways of representing data. Graphs can be used to hide trends in a set of data while asserting to aid the reader visual pattern in complex information. Advanced computer technology has made it possible to produce graphs in one-, two-, and three- dimension. This graph may reflect a different outcome of data they represent when viewed on paper. Features of a graph that may be misleading include the scale, title as well as the margin of error. Large margins of error can result in large discrepancies between the measured units while a biased title may cause incorrect inference.

Graphs can also be abused when its axes are deliberately adjusted so as to depict a preferred trend. This may be augmented with attractive graphics with simple message to deceive the reader. Some of these cases are illustrated in the following graphs.

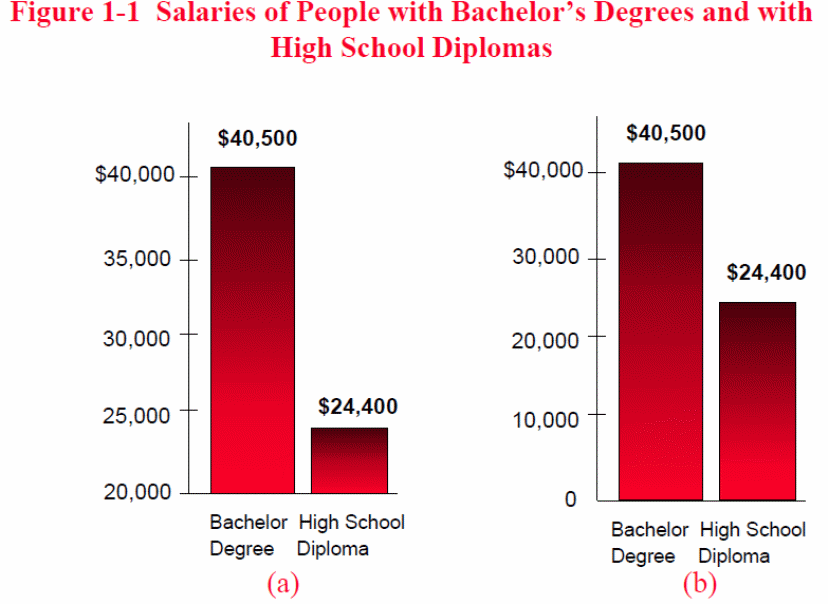
A quick glance at graph (a) may indicate that Bachelor holders earn considerably higher salaries than the diploma workers (over 75% basing on the heights of the bars). However, the same cannot be said of graph (b) where, according to the height of the bars, it appears bachelor holder do not even earn twice as much as diploma holder. The exaggeration of the small difference is primarily due to the scales used for the monetary axis. As shown, graphical data is heavily impacted by the nature of scale used. A zero-origin scale produces a much accurate representation.

Percentages: Misleading or unclear percentages

Percentages can be easily be manipulated to mislead the general population about a specific statistical information. For example, the marketing department of a computer hardware firm may ask twenty of its fifty customers about the performance of a newly introduced printer. If 16 customers praise the product, the company may make a marketing claim that over 80 % of its customers are satisfied or even recommend the product.

Correlation & Causality

Correlation refers to an apparent existence of relationship between two variables. Correlation between two variables has been cited as not to directly signify causality. Causation is defined as the ability of one variable to cause change in the other. Associating correlation with causality is a common mistake and may occur when a researcher ignores statistical facts and employs own preconceptions to make such a deduction. In addition the correlation may be due to a silent third factor that influences the apparent relationship. It can also be as a result of pure chance.

A case in point is a new research that reported a high IQ was found to have increased the likelihood of drug use. The media way of framing the study seems to suggest that there is a strong cause-effect correlation between IQ and drug use. Some may also get the spurious impression that hard drug use is influenced by high IQ although this is necessarily not the case.

This stance was faulted by highlighting the possibility of other social influences such as boredom and peer stigmatization that previous reports indicate gifted children experience. Also, a review of the study methodology and results later showed that the connection was not as strong as reported.

Partial picture

Owing to the impracticality of sampling an entire population, any statistical data only represents a segment of the population at the moment it was compiled. Abuse of statistics arises when such representative accounts are generalized to imply they are the true picture in the whole population. This is common with most official crime statistics. Such statistics is attributed to data gathered by police but it does not illustrate the true level of crime in society because not all crimes are reported to the police.

Deliberate Distortion by subjective selection and omission

Selecting on the information that agrees with the point of view you want to put across is one of the common and effective ways in which statistics is abuse. The author maybe selective in the indicators they choose, the sources of data, the time period used for comparison of the countries, population groups, regions or businesses used as comparisons. The strategy to achieve the desired distortion may involve first drawing up a conclusion or argument and later searching for appropriate data to support it.

Averages

A common average, such as mean can be used to mislead in order to achieve certain goals. For example a car company selling cars that go for $20,000, $32,000, $85,000, $105,000, and $110,000 may claim the firm sells cheaply because the average price is around $70,000. This is not entirely true as a majority of the cars are priced over $85,000.The mean can especially be deceiving for uneven distribution.

Authors can also cause ambiguity when they fail to specify the variation between mean and median in order to project their preferred perspective. Authors may also use subjective definitions of average to mean ‘typical’ such as typical school joining-age hence increasing their scope to be selective and obscure the meaning of ‘average.’

Guess estimates

It is common for media reports to be accompanied by figures, purportedly from credible source, to support their claims. These may take the following forms, “3 million illegal aliens enter US annually;” “Obesity Kills 400,000 Americans annually,” “38% of adults in the United States regularly visit a doctor.”

These figures may be accepted at face-value by laymen readers especially if they are quoted by widely circulated and so called ‘authoritative’ newspapers. In addition, newspaper are not obliged, or even expected to also publish the statistical methodology for the figures. Though such precise numbers are easier to remember and compare, they may be totally misleading. The precise statistics may illustrate a high degree of accuracy which even most advanced methodologies are not capable of attaining. Also, most of these numbers may be far from reality as the scrutiny of the obesity figure in US proved.

Loaded questions

Loaded questions are designed in such a manner that the respondent will inadvertently partly or fully give the desired response after answering it. Loaded questions are common in opinion polls with respondents only allowed a ‘yes’ or ‘no’ answer.

These questions are always characterized by silent presupposed facts but the resultant fallacy will depend on the context in which it is asked. Consider the following questions asked in related surveys:

1. Do you think a person who is suffering unbearably from a terminal illness should be allowed by law to receive medical help to die, if that is what they want?
2. Do you think that a person with an incurable and painful illness from which they will die-for example someone dying of cancer should be able to ask a close relative to end their life. Should the law ever allow the close relative to end their life or not?

For the first question, 82 % of those who responded answered yes. The later had only 44% affirmative responses. It is clear the second question bears negative persuasive/emotional undertones and this could have perhaps influenced the respondents. Use of loaded questions certainly results in skewed results because the connotations of the words used in the question can produce a large variance in the statistical outcome of the survey.

Conclusion

The field of statistics has undergone exponential growth in a few decades to a point where it is applied in virtually all disciplines to make empirical conclusion. If the methodologies of statistical science are followed to the later, it is possible to obtain fairly accurate results.

Also, it is easy to arrive at highly inaccurate and deceiving results which may go unnoticed for a long time. Wrong results can be obtained through sheer manipulation of sample data or research design or it may be due to an unintentional act of improper application of statistical principles.

Abuse of statistics constitutes intentionally manipulating sample data in order to arrive at desired outcomes. This can be achieved through use of among other factors, bad sample, small samples, misleading graphs, misleading percentages, ignoring missing data, flaws in correlation and causality analysis, precise numbers, guess estimates, as well as loaded questions. In order to establish the credibility of statistical allegations, a thorough scrutiny of the underlying inferring principles must be carried out.

Recommendations

In light of the findings of the research the following are recommended:

• Guess estimates: Large numbers should be understood as estimates and should not be taken as factually correct no matter the reputation of the source.
• Misleading graphics/Charts: 3-D graphics and double axis (especially for line graph) should be avoided. For better clarity and avoiding pictorial skewness, 2-D graphs should be used instead. The scale should be carefully chosen so as not to distort the values represented. For precise data points it is advisable to use tables rather than charts.

When studying graphs or charts, attention should be paid to the title, scales and axes. This makes it easy to identify a flawed representation. During mathematical evaluation, an appropriate average (mean, mode, median or quartiles) should be selected depending on the type and nature of distribution of the data. The mean is suitable for an evenly spread-about-the-centre point dataset (e.g. Height and weight). The median is suitable for skewed data (e.g. income and residential prices).Quartiles are best for showing high/low value. Mode can be used to determine the peak (e.g. a popular idea in a poll).

• Causality and correlation: Suggested causal relationship should not be taken unquestioningly. A common-sense approach can also reveal erroneous links between the cause and effect.
• Percentages: For surveys that mostly present their findings in percentages, it will be helpful if additional information is provided. These may include the questions asked, the size of sample, the number of respondents who provided feedback, the modality for selecting participants and the statistical methodologies used to compile the result. The will enable greater scrutiny by outsiders to ascertain their credibility. Finally, apart from the specific measures for some of the abuses briefly outlined above the data used for any inference should bear the greatest degree of accuracy, validity, timeliness, reliability, relevancy and completeness.

Bibliography

Amstrong M. & N. Champigny,’A study on Kringing small block’, CIM Bulletin, vol.82, no. 923, 1989. Web.

Bolton, P., Statistical literacy guide: How to spot spin and inappropriate use of statistics, Parliament. 2010. Web.

Dodhia, R., Misuse of statistics, Raven Analytics, 2007. Web.

Geostatistics: from human error to scientific fraud, Matrix consultant, 2006. Web.

Goldin, R., Are smart kids really more likely to use drugs?, STATS, 2011. Web.

Merks J. W., ‘Abuse of statistics,’ CIM Forum, vol.86. no. 966, 1998, pp. 40.

Merks, J. W., Sampling and statistics explained. Web.

Right To Life Charitable Trust (RTLCT), The use and abuse of statistics in influencing public opinion, RTLCT. Web.

Triola, M. F., Elementary statistics, 8^th edn, Addison Wesley Longman, New York, 2001

Walton, D., ‘Judging how heavily a question is loaded: A pragmatic method’, Inquiry, vol.17, no. 4, 1997. Web.