Abstract
In this research report, the focus of the study will be centered on the topic of geometry, space, manipulative, and technology. The specific discussion is to highlight key topics and organizing the mode of presentation of my work. The main objective is to broaden the understanding of the students in order to achieve the major desired knowledge. In this respect, consistency in the flow of information must be addressed effectively.
The major success tool is to stay focused and to practice professionalism all time during the research presentation. They contain the practical relation of the theory to translate into reasonable outcome of the project research.
Knowledge of solving geometrical problems is very crucial since it involved various methods that are necessary in coming up with viable answer to any mathematical problem. Emphasis on continuous practice by the learner in order to have a better understanding is very crucial as it is the cornerstone of knowledge development in geometry.
Introduction
Mathematics is an important subject that requires a strategic teaching practice, which should be used to ensure effective delivery. In an effort to understand and apply the required teaching strategy, many factors have been raised on suitability of certain effective ways of teaching.
Therefore, it is very important to outline the best practices in teaching and learning mathematics, especially how to approach the topics on space geometry, manipulative, and technology. Moreover, teaching and learning strategies need to be fabricated towards achievement of both immediate and long term goals in mathematics.
This becomes the basis of discussion for this work because it will reveal how geometry helps in understanding environment while in class or any other place. Showing the strategy for teaching geometry, space, and technology involves relating physical things items such as boxes as well as tables. The presentation of facts and ideas is going to be based on smooth flow of information to the end. This is the part of the research that facilitates understanding of the geometry and space.
Mathematics is a subject that involves measurements and relationship of the numbers, symbols, and figures, which help in interpretation of any given value (Carpenter, Hebert, Murray, Wearne, Fuson & Fennena, 2005). Mathematics is a wide concept and it involves sub-branches like geometry, algebra, and other space manipulative.
It involves reasoning and understanding of the values and shapes, depending on the circumstances of presentation. In addition, Mathematics is important because it helps in the analysis and understanding of figures as well as ratios. Therefore, both adult persons and children appreciate mathematics because it is applicable in administration, business, teaching, and understanding the values of finance.
Rationale for the topic chosen
Sometimes, understanding of the subject becomes difficult for the students, even if the teacher can handle several concepts. It is in this regard that there is an urgent need for doing this research in order to come up with alternative ways of handling geometry. The students in most instances need to relate what is contained in the book and the practical approaches to this subject matter.
Importance of the project to my field of discipline
This research project is essential in teaching Mathematics, which is my field of discipline. This is due to the fact that it helps in understanding space geometry, manipulative, and technology, which are some of the core components of mathematics. For instance, the knowledge on how children learn mathematics is vital because it enables better understanding, which makes the teacher know the students’ behavior and generally allow for efficient and appropriate ways of teaching.
Problem explanation
In the mathematical learning process, there is an outline for development of spatial concepts, which create five levels of understanding during the learning of process. According to Van Hiele theory the five levels are grouped as “analysis, visualization, rigor, formal deduction, and informal deduction” (Booker, Bond, Sparrow & Swan, 2010).
This theory also suggested that there is no child who can miss these levels because they are all sequential (Booker, Bond, Sparrow & Swan, 2010). Each level has got its own unique characteristics and contains useful interconnections with one another. These levels are useful in the accounting for effective development of geometric thinking and also in organization of teaching and learning activities.
Background information of the problem
Moreover, children are required to learn mathematics through various methods, which have not been fully explored. Therefore, any child is needed to fully understand various levels, which are essential in learning mathematics.
The first level is recognition or visualization. This level emphasizes that children normally operate, based on appearance of items without reference to their properties. They describe a shape as a whole, but never identify its uniqueness (Reys, Lindquist, Lambdin & Smith, 2009). They relate the object to what it is familiar with. Problems are solved through trial and error or by visual means. However, they still do not have precise language for description generally.
The second level is analysis. This is where the children start to notice and acknowledge the attributes and properties of shapes (Muschla & Gary, 2006).
Possible causes of the problem
The causes for the misunderstanding of mathematical concepts, especially geometry, among children do not lie squarely with the pupils and students alone, but with their tutors as well. This happens because some tutors apply poor strategies in the delivery of mathematical concepts.
There are various strategies that can be used for teaching mathematics, which enable the children to have full understanding of the concepts and get the required knowledge accordingly. The first strategy is constructivist strategy. This approach enables the student to understand any given mathematical concept and apply it reasonably. They are able to create necessary mental image of the topic of learning.
his is done by teaching the children from the perspective of known shapes or issues to the unknown (Deborah, 2009). This is because, by presenting three dimensional shapes first, it will be quite possible to explore knowledge from these familiar objects such as a ball and blocks.
When this strategy is used, then the children will have the opportunity to develop knowledge accordingly. Therefore, the children will learn from known to unknown will be able to understand the concepts effectively. This enables gradual development of skills and learning process (Willis, 2010).
The other strategy involves use of intermediate activities. The intermediate activities involve making students form small groups and solving some problems in form of riddles. When they are learning through riddle, it is very easy to understand what is taught by the teacher. Another strategy is by involving the students in certain advanced activities. The activities will majorly focus on the topic of discussion like describing and sorting shapes. This makes children to be able to describe and identify three dimensional objects.
The other major cause is insufficient resources available for teaching mathematical geometry. This has greatly hindered effective delivery of the required content. Mathematics requires certain resources that guide the proper learning process. The resources for instance, depend on the topic that the students are learning at a particular time (Joanne & Martin, 2007).
In this case, it is crucial to note that learning of geometry and space is guided by use of lines, shapes, and building up of pyramids. Children can learn from models so as to help in understanding mathematics. This resource model may include prisms, boxes, truncated prisms, and development of edge models.
In addition, the models are made from straws, pipe, cleaners or sticks that can be connected with tape or clay (Wilder & Mason, 2005). These enable understanding of the mathematical concepts, and the children are able to draw some useful information from the figures. Plain drawing papers are also useful, especially when they are introduced in drawing of shapes.
Children can draw something they know from circles, triangles, and rectangles (National Library of Virtual Manipulative, 2010). They will be able identify the number of sides that each figure has. The learning resources should be present at all times when teaching mathematical geometry. Therefore, children will have a better understanding of the concepts and to be able to apply the knowledge relatively based on the provided circumstances in life.
Literature review
According to National Research council and committee on early childhood mathematics (2009), it was proposed that development on use of geometrical mathematics to teach younger children on construction of shapes in a classroom setting by use of free materials, which included use of clay, boxes, and cartons. Construction with papers through folding, drawing shapes, and patterns. These were very practical in enabling the children to understand the shapes and apply them appropriately.
Geometry for instance enables the children to understand real objects that reflect shapes of objects. These include polygons and other patterns, which are useful in the child’s learning process.
Wilder and Mason found that the other major use and application of geometry and shapes include location and associated representations (Wilder & Mason, 2005). Location and movement describe directions, distance, and position. The same findings were also supported by Joanne and Martin who have viewed that this observation enables the children to describe their world and understand the surrounding (Joanne & Martin, 2007).
In addition, Sweeney, Ray, and Arthur postulated that the students are able to build mathematical concepts like positive and negative numbers plus skills relating to other subjects (Sweeney, Ray & Arthur, 2008). The committee also ascertained that geometry also enables the understanding of patterns and transformations (“National Research council and committee on early childhood mathematics”, 2009).
In sum, this literature review is practical and relevant to the research problem since teaching and understanding geometrical mathematics has been a major problem among the school-going children. Therefore, this section of the paper highlights some of practical overviews regarding this research problem. In essence, children ought to be exposed to geometry and taught relevant mathematical skills and concept at very young ages. This is crucial because it helps children in knowing basic concepts of geometry (Carsrud & Brännback, 2011).
Preliminary reference list
This research report has widely made use of 15 academic sources, which are relevant to the problem of study. These sources have been extensively sourced and acknowledged. The sources are listed in the reference page of this report.
Research questions
The study aims to address the following questions:
- What are the causes of poor performance in geometry and space among children?
- What strategies are required in teaching mathematics?
- Which strategies should be employed in teaching geometrical mathematics?
Methodology used
This part of the report involves evaluation of methods and tools employed in the research. Besides, data validity and integrity will be analyzed.
Evaluation methods and tools
The research philosophy and stance focus on embracing elements of geometrical mathematics among children. It is assumed that the subject under study is not only observable, but can be measured to some extent. This is due to the fact that geometrical shapes can be seen and recognized among children.
Therefore, this research intends to carefully isolate facts, feelings, and meanings, which are evaluated against geometrical objects (Carsrud & Brännback, 2011). In addition, this research context has attempted to identify some of the underlying factors, which have contributed to poor performance in geometry and space mathematics, among pupils as well as students.
These factors have been described as causal rather than merely descriptive or explanatory. Questionnaires are going to be used in this study so as to help in collecting data. Statistical tools are appropriate in analyzing the findings from this study.
Reliability and validity of the evaluation methods and tools you used
Moreover, representative sample will be chosen for this study, which is more reliable and valid. Besides, methods and tools such will be tested and re-evaluated for reliability and validity. Those ones which fail to meet the research expectations will be dropped, and the most appropriate tools and methods are to be adopted.
Maintaining integrity of collected data
This will be ensured by maintaining accuracy of the data collected. Recording of data must be consistent to avoid any form of bias reporting.
Research Design
Amongst the various research designs available for study, this research will be designed in the form of a questionnaire. The primary data collected will be obtained through the structured questionnaires that are administered to the respondents via phones, one-on-one, internet, and posts (Cary & Nick, 2008). Under this section of the report, purposive sampling techniques can be chosen for the study.
Research method explanation
The research is primarily a quantitative study, which will tend to develop recommendation and conclusions from the statistical analysis of the data collected. The objective of a quantitative study is to classify features that are associated with the phenomena being addressed by the study, to obtain a figure of the features as well as constructing statistical models, which are important, as they will aid in explanation of the nature and occurrence of the phenomenon.
Still, the one conducting this research has wide knowledge on what he aims to discover. In addition, this quantitative research design will help the researcher, as it will allow development of tools for the study prior to collection of data. As such, the best data collection tools will be questioners as well as interviews (Dickson, Chiu & Hung, 2010). Therefore, this is what motivated the researcher to choose this quantitative design for the study.
The quantitative techniques and methods used in this research are more appropriate since they can be subjected to statistical techniques such as regression analysis. However, deviations and variances were realized in this research work due to approximation methods such as regression analysis. Such statistical estimates made the actual results to differ from the planned outcome.
The participants interviewed in this research work were mainly children in primary, high school, and middle-level colleges. This was so because they were the focus population in this report. In fact, only handful tutors from both primary and high schools were interviewed on the research problem.
Permission
This was obtained through formal letters addressed to the concerned parties used in this research. Such formal requests made it easy to obtain the required information.
Data presentation, findings, and analysis
The questionnaires, which are already filled, will be scrutinized to identify errors. Rejection criteria will be; those questionnaires with a significant number of errors, which are capable of influencing the results in a biased manner, will be rejected. After scrutinizing them and eliminating the flawed ones, the rest will be inputted into a computer to form the researcher database (Cary & Nick, 2008). The following statistical finds can be generated for this research work.
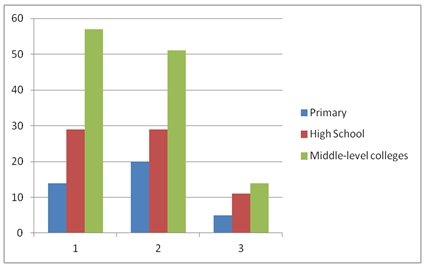
Suppose, a research was conducted in area A regarding the causes of failure among children in geometrical mathematics, the above data could be obtained. This shows that the main causes are attributed to inappropriate strategies employed by tutors in teaching mathematics. This is an area of research that demands some improvements (Taylor, 2005).
Implications and limitations
The research found its strength in data presentation and report findings. Besides, literature review on the problem was given much attention and focus. However, the weakness of the research is on the inadequacy of statistical tools and analysis. More quantitative methods such as and chi-square techniques could help in analyzing the degree of association between the students failures and poor teaching strategies (Taylor, 2005).
Problems such as unresponsiveness among the respondents hindered effective delivery of the best quality research findings. Some of the respondents were even unwilling to co-orate with the interviewer. Such limitations of data and biased responses led to skewed report generated from the data. Some of the data collecting instruments were also found to be faulty, in the course of the study.
Conclusions and Recommendations
In sum, appropriate strategies and resources should be employed in teaching geometry among children. This was the center of this research work. However, weaknesses were witnessed in insufficient statistical presentation and analysis. This is an area that ought to be given much emphasis in the next research.
The unresponsive respondents can be well managed through the adoption of the participant observation method, which makes the researcher to identify with the rest of the team. This facilitates collection of data, without the knowledge of the respondents. They will not be in a position to know that they are being interviewed in the process. In case, this research is to be conducted once more, it will be done differently.
This can be done through intensive literature review on the problem. In addition, more statistics will be gathered for analysis so as to provide a more refined report. Finally, it is important to mention that master’s skills has facilitated refined research, by incorporating advanced statistical tools employed in quantitative studies.
References
Booker, G., Bond, D., Sparrow, L., & Swan, P. (2010). Teaching Primary Mathematics (4th Ed.). Frenchs Forest, NSW: Pearson Australia.
Carpenter, P., Hebert, J., Murray H., Wearne, D., Fuson, C. & Fennena, E. (2005). Making Sense: Teaching and Learning Mathematics. Portsmouth: Heinemann Publishers.
Carsrud, A. & Brännback, M. (2011). Understanding Family Businesses: Undiscovered Approaches, Unique. New York: Springer.
Cary, K. & Nick, R. (2008). Sustainable investing: the art of long-term performance Oxford: Earthscan.
Deborah, M. (2009). Strategies for Teaching Mathematics. Huntington Beach: Shell Education Publisher.
Dickson, W. Chiu, L. & Hung, P. (2010). Service Intelligence and Service Science: Evolutionary. Hershey: Idea Group Inc.
Joanne, P. & Martin, K. (2007). Supporting Mathematical Learning: Effective Instruction, Assessment and student Activities. San Francisco: Jossey- Bass.
Muschla, A. & Gary, R. (2006). Hands- On Math Projects with Real Life Applications. San Francisco: Jossey- Bass.
National Library of Virtual Manipulatives (2012). Web.
National Research Council & Committee on Early Childhood Mathematics (2009). Mathematics Learning in Early Childhood. Washington DC: National Academies Press.
Reys, R., Lindquist, M., Lambdin, D., & Smith, N. (2009). Helping Children Learn Mathematics (9th Ed.). New York, NY: John Wiley & Sons.
Sweeney, J., Ray, D. & Arthur, T. (2008). Statistics for business and economics. Mason: Cengage Learning.
Taylor, G. (2005). Integrating quantitative and qualitative methods in research. New York: University Press of America.
Wilder, J. & Mason, J. (2005). Developing Thinking in Geometry. California: Sage Publications Ltd.
Willis, J. (2010). Learning to Love Mathematics: Teaching Strategies that Change Student Attitudes and Get Results. Alexandria: Association for Supervision& Curriculum Development.