Introduction
Needs and learner analysis involves the systematic assessment of a lesson to determine the actual problem for which instruction is the solution. Educators employ the approach to understand the problems faced by learners and design practical educational programs that solve these challenges. Ultimately, resolution programs that target particular documented needs are marketable and applicable. They enable educators to make informed decisions and plans about teaching content, thus extending the impact and reach of education. This research conducts a needs and learner analysis of the selected introduction to calculus lesson. It provides the different approaches used to ensure that the developed instructional plan is suitable for the students.
Needs Analysis
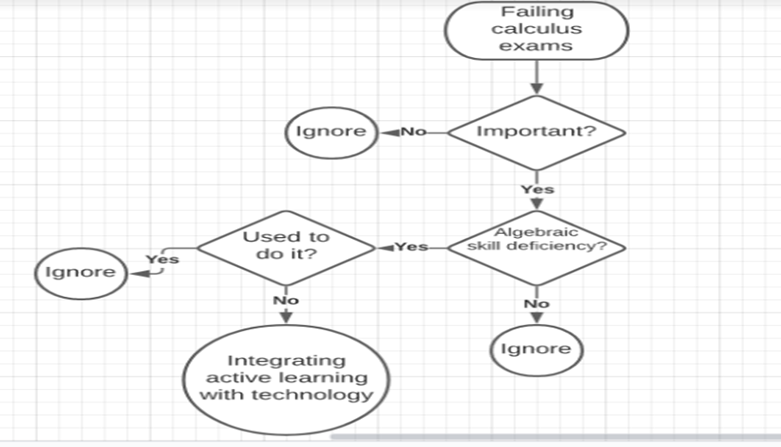
The significance of needs analysis for an introduction to calculus class is that it establishes the relevant requirements of the lesson by identifying the problems affecting performance. According to Mager (1989), a needs analysis should be conducted in twelve different steps, which focus on the critical needs with the most substantial implication to the students. The first step of Mager’s performance assessment is determining the group whose performance is being scrutinized. Specifically, first years doing mathematics-related courses are the targeted audience for this analysis. The second step is describing the negative behavior that results to the problem of failure. Although freshman learners seem prepared to handle the class initially, they often experience difficulties with the subject, which raises concerns. The students do not master all processes involved in finding derivatives of functions and utilize high-level monitoring systems to estimate these figures (Gordon, 2022). As a result, even though they know what is expected of them, they are still unable to complete tasks correctly, thus failing exams. Thirdly, since the calculus topic is introduced in some high schools, learners should excel in the first-year examination.
In the fourth step of the assessment, the cost of the discrepancy is evaluated. Failure to master the introduction to calculus concepts is likely to affect the performance of mathematics students because they are required to apply these processes in upcoming semesters. In the subsequent stage, Mager suggests that the process stops if the discrepancy’s cost is negligible. However, the implication of this problem is significant because not passing the unit disqualifies one from majoring in STEM sectors. Since calculus 1 is among the classes with high withdrawal and failure rates in universities and colleges, the consequences of this problem affect students, campus systems, and the nation. Since failure thwarts many promising engineers and scientists, the cost of this challenge is significant enough to warrant research and the establishment of possible resolutions (Gordon, 2022). Therefore, the evaluation proceeds to the next step, which involves establishing whether the learners know what is expected of them. Most first-year students do not understand why they follow specific algebraic processes in estimating derivatives of functions. Therefore, the primary cause of failure is not comprehending the algebra and arithmetic associated with the calculus lesson.
Next, since the learners do not know how to do what is expected of them, the seventh step of determining the consequences of underperforming is skipped. Students are not equipped with adequate skills from high school to understand and apply the mathematics that underlies algebraic manipulations. The following level eight discusses how the task can be simplified for learners to master it. To simplify the task and enhance mastery, educators should focus more time and resources on uncovering the misinformation that resulted in calculation errors and replacing them with accurate scientific understandings (Brezavšček et al., 2020). Algebraic skills are often used in a calculus 1 lesson because they are a prerequisite in finding derivatives of functions and, therefore, students should master it. Students have a great potential to gain algebraic skills through understanding their theoretical underpinnings, getting the step-by-step processes to be followed, and organizing their work well to avoid mistakes.
Success in the introduction to calculus lesson familiarizes students with concepts and formulas that underpin function derivatives, ensuring students pass subsequent related courses. As a result, there will be equitable science and engineering opportunities for coming generations, and the economy will thrive. Following the aforementioned responses, the subsequent step involves drafting potential solutions. One resolution to this problem is changing the K-12 curriculum framework so that students take similar mathematics classes in high school sophomore year. Secondly, introducing equal advanced placement math and calculus courses in high school reduces the gap between ill-prepared students and experienced learners in calculus. Lastly, educators can integrate active learning and technology in the present lecture and test strategy to enhance algebraic skill development (Hite et al., 2021).
In stage ten, educators are required to estimate the cost of implementing the various solutions. Introducing calculus in high school is challenging because it will mean rushing students into advanced mathematics, yet they need more foundational arithmetic. Further, equalizing learners’ paths will restrain some advanced students who want to go beyond. Finally, instructors compare the cost of the solutions to the problem’s impact and select the most suitable recommendation in phase eleven and twelve of the analysis. Since incorporating calculus lessons in high school has discrepancies and does not predict the success of the introduction class, integrating knowledge and software is the most practical and less costly recommendation.
Learner Analysis
Educators should design lessons that best suit the needs of students. To do this, they must understand the learners and their needs through learner analysis. Critical aspects of the assessment include learner characteristics, prior knowledge, demographics, and access to technology. The general behavior exhibited by students in an introduction to calculus lesson is that they are anxious, quick, motivated, interested in the subject, and have a positive attitude towards the learning (Wintarti & Fardah, 2019). The students believe that calculus problems are easy to solve because they need straightforward applications of formulas or algorithms. The learners are first-year undergraduates who grasp concepts quickly and have good retention abilities. However, they do not recognize the significance of critical thinking in relating class principles to real-life situations.
Since pre-calculus was introduced in high school, most students are familiar with fundamental theorems and rules. Therefore, the entry skills of the lesson are trigonometry, algebra, and geometry skills. However, existing data reveals that most learners lack vital algebra skills, which is a weakness. The difference between students is that some have mastered basic concepts taught in high school pre-calculus while others have not. Students join the introductory class because it forms the foundation of subsequent science, mathematics, and engineering units. The learning styles employed by most learners enrolled in the lesson are active and student-centered. Lastly, introduction to calculus students can access institutions’ technology, including SimCalc and CAS technologies. Therefore, visualizing graphs and curves related to algebraic functions is simplified for them (Tatar et al., 2020) The iterative process that conjoins these critical learner aspects informs significant instructional design decisions. It enables educators to tailor teaching based on the existing student knowledge to control their learning and gain a deeper understanding of class content.
Conclusion
Conclusively, conducting needs and learner analysis establishes a method for exploring what has been covered in a lesson and what gaps exist in the learning process. The assessments offer insights on the most challenging concepts in the introduction to calculus lesson. Subsequently, an integrated instructional design is recommended to enhance mastery and understanding of the processes, formulas, and representations involved. Ultimately, understanding and passing the introduction to calculus exam guarantees a smooth application and transition to other complex calculus units.
References
Brezavšček, A., Jerebic, J., Rus, G., & Žnidaršič, A. (2020). Factors influencing mathematics achievement of university students of social sciences.Mathematics, 8(12), 2134. Web.
David, E., Hah Roh, K., & Sellers, M. (2020). Teaching the representations of concepts in Calculus: The case of the Intermediate Value Theorem.PRIMUS, 30(2), 191-210. Web.
Gordon, L. (2022). High calculus failure rates thwart students across CSU.EdSource. Web.
Hite, R., Johnson, L., Velasco, R., Williams, G., & Griffith, K. (2021). Supporting undergraduate STEM education: Perspectives from faculty mentors and learning assistants in calculus II.Education Sciences, 11(3), 143. Web.
Tatar, D., Roschelle, J., & Hegedus, S. (2020). SimCalc: Democratizing access to advanced mathematics (1992–present). In Historical instructional design cases (pp. 283-314). Routledge.
Wintarti, A., & Fardah, D. (2019). The instructional design of blended learning on differential calculus using successive approximation model.Journal of Physics: Conference Series, 1417 (1), 012064. Web.