Introduction
The current astronomical standing that astronomical objects are billions of years from the Earth suggests and upholds the view that the entire universe may be much older than previously hypothesized by former theorists ( 1 light year = 9.5 X 1012 km). This hypothesis follows from the logical fact that if the light from these astronomical objects needs billion of years to reach the earth, then as a matter of consequence, the age of the entire universe must be of the domain of billions of years.
It goes without saying that the scepticism of many people who are opposed to this hypothesis is anchored on their doubts about the accuracy of the scientific methods employed in measuring astronomical distances (Feuerbacher, 2003, p. 1). Thus, a great number of folks settle for the former young-earth creationists’ view that almost all the astronomical objects observable in space are within the proximity of the Earth. This study seeks to clear the air on some of the disputable items by describing the methods which are used to measure astronomical distances.
A Holistic Outline
In determining astronomical distances, different methods are employed, which generally portrays a symbol of a ‘ladder’ with each approach serving as a tool for measuring a specific range of distance in space. Again, the consecutive methods are based on the immediately previous method as a standard unit of measurement. The very initial standard unit of astronomical measurements is the Earth’s distance in relation to the sun which is approximately one hundred and fifty million kilometres, and this is the initial reference unit referred to as 1 AU (one astronomical unit).
Following this stage in the ladder of astronomical measurement method is a set of simple geometric techniques with which one can measure astronomical distances up to hundreds of light-years. This would form the basis for photometry and spectroscopic techniques of measuring astronomical distances under which the ‘Hertz sprung-Russell diagram’ would be considered. The method of using ‘standard candles’ for the measurement of larger distances in space will be explored, and lastly, a description of the Cosmological Red Shift and the Hubble Relation which are employed in determining very large distances ( that is, distances in the tune of billions of light-years) will be done.
Geometric Methods
The astronomical distance to those stars which are within the proximity of the earth is determined trigonometrically using the data obtained from the parallaxes of the stars. This method can be illustrated by a simple analogy by observing ones finger with either one eye and then with the other eye against some background material. One will notice that the stationary finger appears to move relative to the eye, which is observing it (Wright, 2007, p.1). This follows immediately from the fact that the eyes’ line of sight differs from that of the right eye to that of the left eye.
The position of the finger with reference to the position of one’s nose is the main determinant factor in establishing the angle swept by the eye in seeing the finger. As a matter of fact, the angle reduces as the distance of the finger from the nose lengthens and vice versa. The alternative implication of this is that the distance can be determined by applying trigonometric principles to the angle. In this illustration, the distance between one’s eyes is referred to as the baseline, while the angle difference is known as the parallax.
Since the stars are very far from the earth, their parallax is infinitesimal for the baseline from one eye to the other is very short. This is simply done by recording the angle of inclination of a specific star in space during summer and similarly during winter. The calculated angle difference between the two recorded observations represents the parallax for the star (Atkinson, 2009, p. 1). Having this angle difference (parallax) and the length of the baseline as 2 AU, one can easily calculate the astronomical distance to that specific star by employing the relevant trigonometric ratio, as shown below.
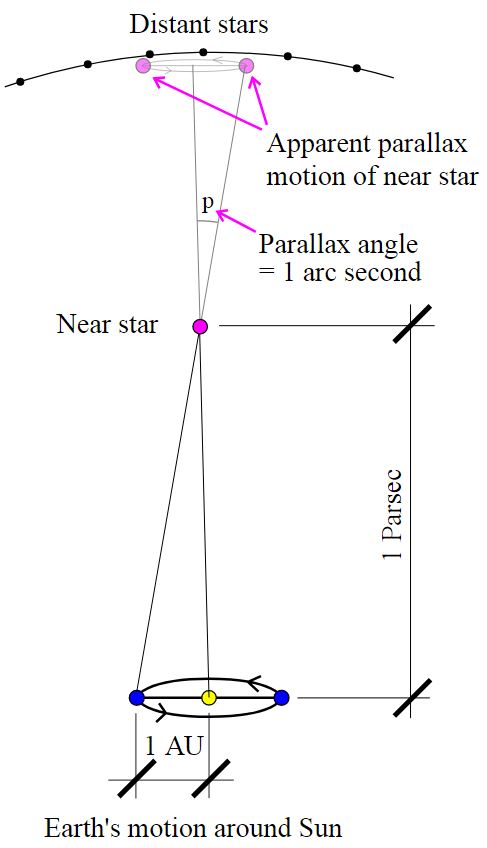
Parsec indicates the distance of an astronomical object. One arc second = 1/60 of an arc minute, one arc minute = 1/60 of a degree. Since the astronomical range is inversely proportional to the parallax, an astronomical object with a parallax of w arc minutes would be 2/w parmin away which is equivalent to 1/30w parsec away. The other equivalent conversions of one parsec are;
1 parsec = 3.09 X 1013 km = 206000 AU = 3.26 light-years.
From the preceding analysis, the annual parallax which denotes the angle difference as observed from the sun and the earth rather than the angle difference as observed from the earth during the summer and the winter can easily be deduced as half of the aforementioned parallax (Strobe, 2001, p. 3).
Measurements
The astronomical distance between the earth and all the stars within our proximity is way above one parsec and with the inverse proportionality; the respective parallaxes are way below one arc second. For accurate measurement of such minute angles, astronomical tools and equipment of high precision are used. Wilhelm Bessel was the pioneering astronomer in this field when in 1838, he estimated a distance of about ten light-years for one of the stars in space.
Since Bessel’s moments, the precision of astronomical measurements has improved by a very great margin with the errors arising from position fluctuation due to atmospheric challenges of the earth being corrected by the launch of satellite observatory centres. For instance, the satellite Hipparcos has recorded the parallaxes of around one hundred and twenty thousand stars with such a superb precision of 0.97 milliarcseconds and with an estimated distance of data collection standing at about one thousand six hundred and thirty light-years from the earth. The launch of yet another satellite, Gaia in 2010, was anticipated with projected astronomical distance reliability of close to thirty-three thousand light-years.
Current developments in electromagnetic waves have bequeathed astronomical inquiries with the ready tool- radio waves in place of the visible light for more accurate and precise astronomical measurements (Adcock, 2010, p. 1). Very Long Baseline Interferometry is the technique employed in such scenarios which encompass the use of two radio telescopes having a long-distance of separation between them.
They are more precise in that their precision is estimated to be in the tune of one hundred micro arc seconds. This technique has proved to be indispensable in the measurement of very large astronomical distances. For instance, the method has been used in determining the distance to pulsars. The technique has the honour of registering distances way over eight thousand light-years and hence supporting the hypothesis that the universe is much older than six thousand years as it was previously supposed.
Spectroscopic Method
Spectroscopy refers to the method by which the brightness of astronomical bodies is determined, and it finds its application in measuring the distance of those astronomical bodies whose parallaxes cannot be established. It is well known from the inverse square law that the brightness of any luminous body or a good reflector is directly opposite to the square separating the observer and the body. However, according to the laws of relativity, this law must be adjusted a little to accommodate the entire universe. The adjustments are of little relevance for all astronomical bodies in the Milky Way galaxy and in those galaxies within its proximity.
With the inverse square law, we only need to establish the brightness of an astronomical body at a fixed range of distance as our reference and relate this to the recorded brightness of the astronomical body as observed from the earth, and then we would be able to tell the distance of the body from the earth (Genseberger, 2001, p. 1). The Absolute brightness of an astronomical object is the name given to the standard range of distance, and it is taken to be 10 parsecs while the real brightness recorded as observations are made on the earth’s surface is the apparent brightness.
Therefore, the only challenge which needs to be tackled is: How can the absolute brightness of an astronomical body be determined if its real distance is yet to be established? Spectroscopy offers the solution to this challenge, whereby, an analysis of the spectra of the astronomical bodies whose parallaxes can be determined and are within the proximity of the body under investigation.
The dark colours that are noticeable in astronomical bodies indicate that the colours emitted by light are much less than those of other wavelengths. This is because each subset of an atom within an astronomical body can only absorb a specified wavelength (Kincaid, 2011, p. 1). In the event that the atoms are energized, they release the same wavelengths, and therefore one can easily establish the spectral lines corresponding to each element.
This forms the foundation stone upon which all stars are classified into groups referred to as spectral classes in which stars categorized in the same class share the same pattern of dark spectral lines which reflect a similar abundance of elements in their respective atmospheres. The spectral categories and groups are listed and distinguished from each other by the use of capital letters.
The Hertz sprung-Russell diagram
A graph of the stars whose distance has been established from their parallaxes and whose absolute brightness can be deduced in a diagram is mainly a narrow line where one of the axes represents the spectral class, and the other axis represents the absolute brightness. This implies that the two variables are directly proportional and in the event that one establishes the spectral class/colour of a certain star, then one can easily find its absolute brightness. Hertz sprung-Russell diagram is the name given to one such a graph named after the two astronomers who put it forth.
A comparison of two Hertz sprung – Russell diagrams for both the absolute brightness and the apparent brightness against the spectral class of a certain star in a stellar cluster, enables one to derive a constant ratio relating the two which gives a reflection of the actual distance to the stellar cluster upon computations aided by the observed parallaxes of nearby stars.
Standard candles and astronomical distances
From the inverse square law, clear observation of very weak stars which are at a very great distance from the observer cannot be done. Nonetheless, some astronomical objects in space whose absolute brightness can be determined without necessarily measuring their distances are taken as reference objects and are known as standard candles. The most common of these standard candles are Cepheid and Supernovae (Lima, 2011, p. 1).
To determine the astronomical distance of a stellar cluster or a galaxy, one should locate several Cepheids in it since they are very bright, record the periodic oscillations and harness this relationship to deduce the absolute brightness of the Cepheids (that is the standard candles). A comparison of the deduced absolute brightness with the apparent brightness leads one to the establishment of the distance to the cluster. With the aid of the Hipparcos satellite Cepheid, parallaxes can now be determined with a very high degree of precision which is an indispensable ingredient in measuring the relationship between the periodic oscillations and the absolute brightness of the Cepheid. This method is effective in measuring the distance to stellar clusters which are within the range of tens of a million light-years from the earth.
Towards the end of the lifecycle of certain stars, the stars undergo massive and spontaneous explosions and hence emit an enormously bright light which forms the second prominent group of the standard candle, the supernovae. Supernovae are therefore much more effective in determining very great astronomical distances as compared to Cepheid since they are known to measure the distance to galaxies which are within the range of hundreds of a million light-years from the earth.
Cosmological Red Shift
A close investigation into the spectra of distant galaxies (way above one million light-years), reveals that the general appearance of the spectral lines of elements is a little maladjusted in that, all the spectral lines appear to have been shifted to a longer wavelength than the normal one. Since the red light is characterized by the longest wavelength, then the shift is said to be inclined towards the red light resulting in the red name shift (Lima, 2011, p. 1). Additionally, an investigative examination into the magnitude by which all the spectral lines are shifted reveals that their relative shift is similar.
Doppler Effect explains this shift in that there must be some relative motion of the galaxies with reference to the observer. The redshift signifies that the galaxies are moving away from the Milky Way galaxy while a blue shift reveals that the galaxy gets closer to the Milky Way galaxy such as the Andromeda galaxy.
In 1929, Hubble discovered that the redshift (and consequently the velocity with which galaxies move away from the Milky Way galaxy) is directly proportional to the astronomical range of separation from us, leading to the formulation of the relation;
V = H x d, from which the astronomical distance d can be computed.
Where v is the velocity of retreat in m/s, H is the Hubble constant which is given by 70 km/s/million parsec and d is the distance in parsec.
Reference List
Adcock, George. (2010). Astronomical distance measurements. Web.
Atkinson, Nancy. (2009). Astronomers find new way to measure cosmic distances. Web.
Feuerbacher, Bjorn. (2003). Determining distances to astronomical objects. Web.
Genseberger, Rupert. (2001). Measuring distances by parallax method. Web.
Kincaid, Jane. (2011). Distance to the sun. Web.
Lima, Damian. (2011). How we measure distances to stars and galaxies. Web.
Strobe, Nick. (2001). Distances—inverse square law. Web.
Wright, Edward. (2007). The ABCs of distances. Web.