Summary of Studies
The central issue of this study was an attempt to determine the statistical relationship between the students’ perception of teachers’ beauty and the quality of academic teaching. In this paper, Hamermesh and Parker (2005) take a multi-factor statistical analysis approach to eliminate potential errors. The results of this study suggest that the higher the teacher’s beauty rate, the higher their course rating. In other words, better-looking university employees get more favorable feedback on the quality of their work, which, ultimately affects salary levels.
The structure of this research article includes four sections: introduction, discussion of the teaching beauty and measuring, demonstration of the results obtained, and a section of conclusions. In the introduction, the authors point out the lack of up-to-date data on the relationship understudy in a wide range of academic literature and propose the hypothesis that beauty has the potential to improve student assessment of teachers’ work. The second section is devoted to establishing the framework for the experiment: in particular, 94 teachers from the University of Texas, from all academic levels, were selected for the main observation by 463 university courses (16 957 participants) assessed their performance, after which quantitative results were subjected to regression analysis using the least-squares method. For a first trial based on a discussion of teachers’ photographs, descriptive statistics using the weighted average was gathered, including gender, minority, origin, work schedule, class credits, and audience for which the professional works. As part of this section, studies were carried out on the photographs of employees by six students, ranked according to gender and level: three of each gender, two of whom are graduating students. The authors, for the first time, speak out about the potential threat of significant differences in the assessment of the beauty and quality of the work of male and female teachers. Verification of the results is carried out by determining the Kolmogorov–Smirnov test (0.077) and Cronbach’s alpha (0.62).
The third section invites the readers to familiarise themselves with the main results of the survey regarding students’ sympathy for the quality of teaching work. Specifically, the authors used the WLS method to compare the scores between the correlation variables were divided into two vectors: X was data about the teacher, and Z was about the course. In the first place, employees from the social minority category receive less student approval than most teachers (-0.249). The same effect is observed for workers whose native language is not English (-0.253). In addition, one-credit participants in low divisions receive significantly higher scores from students (0.687). It is worth admitting that the key finding of the researchers is that female teachers are getting significantly lower results than males, which is 0.128 versus 0.384. During calculations, there were fears about the potential effect of a ceiling for which elimination of the LAD method as an alternative has been used: yet, results practically have not changed.
The authors have identified four potential problems that could affect the outcome of the study: the difficulty of determining physical beauty when using nice, official clothes and makeup (0.229); picture quality (0.267); the error of sampling (0.236); asymmetrical effects of beauty (0.237 versus -0.318); and the impact of the composition and complexity of the course on the evaluation (0.177). For each of these problems, the authors conducted a sub-test that showed the degree of statistical significance: a reassessment was made based on the required criterion from a sample. Hamermesh and Parker argue that the beauty of the worker does indeed increase the academic scores of students. Moreover, the authors suggest that this effect increases overall productivity.
Evaluation of Statistical Results
This section of the coursework provides descriptive answers to three questions asked about the quality of statistical analysis in the study. It should be mentioned that all questions refer to the main results table, which contains data from the course survey of students and critical determinants: in the article, this table is the third and is located on page 372.
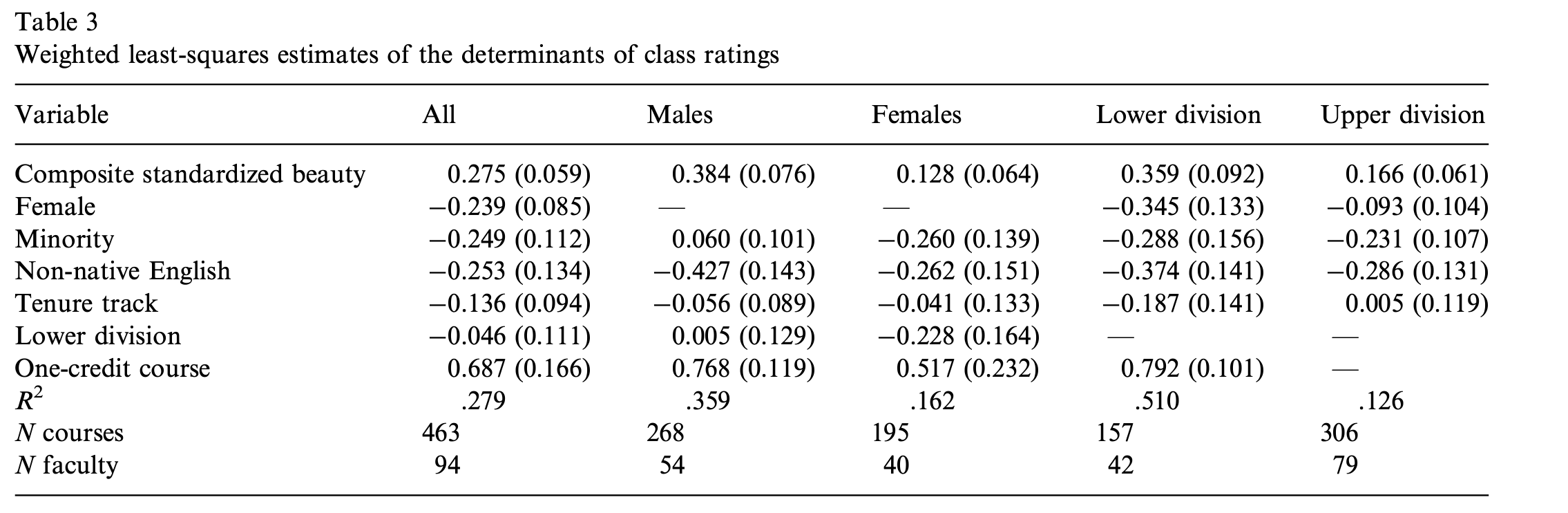
As can be seen from the bottom rows, there is the determination coefficient R2, which is responsible for the reliability of the used regression method. In other words, this index is a statistical indicator, which can be used to determine how much the regression equation corresponds to real data: if the coefficient is close to 1, it indicates high efficiency and importance of the model, and vice versa, if it is close to 0, the regression model is not very significant. It is noticeable that the highest R2 is typical for the estimates obtained from students of low divisions: is 0.510. At the same time, estimates from students of high divisions are least significant, which may be caused by a number of accompanying variables.
It should be admitted that the spectrum of variables is independent so that none of the determinants is directly dependent on the other variable. It means that exclusion of one of the regressors according to this principle is impossible. However, if one pays attention to weighted average values, one can find out that this number is the smallest for the tenure track (-0.136): apparently, this regressor can be excluded without the probability of significant influence on the final result.
For the differences between male and female teachers in this regression analysis to be more evident, the regression model needs to be changed. In particular, the weighted least squares method can be changed to a least absolute deviations model: given that y- and x- values already exist (as shown in Figure 1), researchers can convert the data into the proposed model, and this step will make the results more plausible. To determine the confidence intervals for regression data, Student t-tests have traditionally been used, which requires setting the level of significance and the number of degrees of freedom. In addition, regression coefficient values are used as variables for the t-test.
Reference List
Hamermesh, D.S. and Parker, A. (2005) ‘Beauty in the classroom: Instructors’ pulchritude and putative pedagogical productivity,’ Economics of Education Review, 24(4), pp. 369-376