Introduction
The Multiple linear regression analysis of multiple imputation approach was employed to satisfy the research goals. Multivariate Multiple Linear Regression will be used to determine the connection between the variables (Gao et al., 2022). It is a statistical test that uses one or more other factors to predict several result variables. It is also utilized to figure out what the numerical relationship is between these variables and others. The variable to be predicted should be continuous, and the data should match the multiple linear regression assumptions. The variables must be independent, the outcome variable must have a linear connection, the residuals must have a normal distribution, and the variance of the residuals must be homoscedastic.
Discussion
Furthermore, the step selection approach will be employed to obtain the relevant and crucial predicted variables. Except for the response “YKappa,” the dataset has some missing values in each variable; consequently, the author will use a Gao’s (2022) test statistic to evaluate what sort of missing data is there and whether the data is missing entirely at random (MCAR). The quantity of information that may be exchanged across variables is influenced by the missing data pattern. If additional variables for the instances to be imputed are not missing, imputation can be more exact. It’s also true in the other direction. If predictors have been non-missing in rows that are massively incomplete, they have the potential to be more strong.
The missing values in each variable will then be filled using multiple imputation. The Multiple Imputation by Chained Equations (MICE) package offers numerous methods for finding the missing data pattern(s) in a dataset, in addition to doing imputations. Various Imputation: We estimate multiple probable values for the data points based on the distribution of the observed data/variables. This allows us to account for the uncertainty surrounding the genuine value and generate unbiased estimates that are close to the true value (under certain conditions).
Furthermore, accounting for uncertainty allows us to calculate standard errors around estimations, resulting in a more accurate sense of the analyses’ uncertainty. This approach is also more versatile since it can be used with any type of data and analysis, and the researcher may choose how many imputations are required for the data at hand; in this case, the researcher will utilize five imputations.
The five-step technique for impugning missing data is as follows:
- Use an appropriate model that contains random variation to impute the missing variables.
- Repeat step 1 3-5 times more.
- Use conventional, comprehensive data techniques to do the appropriate analysis on each data collection.
- To generate a single point estimate, average the values of the parameter estimations over the missing value samples.
- Average the squared standard errors of the missing value estimations yields the standard errors. After that, the researcher must determine the missing value parameter’s mean and variance across all samples. Finally, to determine the standard errors, the researcher must mix the two values in multiple imputation for missing data.
Our regression model will be estimated independently for each imputed dataset, 1 through 5. The estimates must then be summed or pooled to provide a single set of parameter estimations.
Analysis Results
The author first verified the four assumptions, and the data did not fulfill all of the requirements. The answers (errors) are normal, independent, and have a constant variance, but the relationship between them is non-linear. After the log transformation on the answer “YKappa,” the assumptions were improved.
To get the relevant predicted variables, the following research phase selection approach was used. The classic variable selection approach, stepwise selection, was one of them. ChipRate, BFCMratio, TlowerE2, UCZAA, AAWood4, SteamF4, UpperHT3, WeakLiF, BlackFlow2, SteamHF3 were significant predictors with p-values less than 0.05 (Marcelo et al., 2018). The assumptions were then tested by repeating multivariate linear regression with the 10 predictors.
The null hypothesis was rejected using Little’s test since the chi-squared value was 217.2 and the p-value was very tiny. As a result, the author determined that the values were missing totally at random (MCAR).
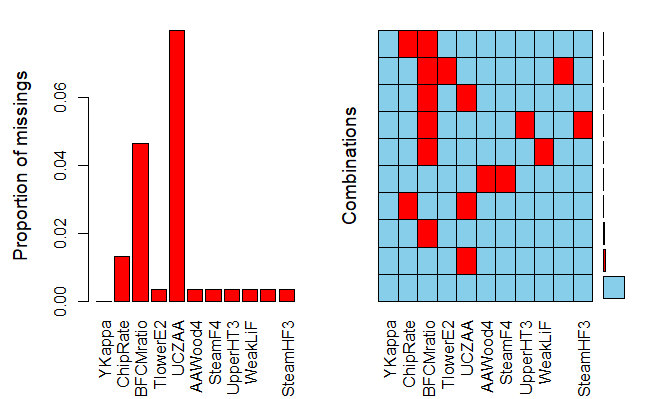
Five imputed datasets were constructed using multiple imputation. “pmm” was used to impute missing values for our 10 variables. Our variables of interest are now configured to be imputed using the imputation technique we defined, as seen below. The method matrix’s empty cells indicate that those variables will not be imputed. Variables with no missing values are set to be empty by default.
Conclusion
There are currently five imputed datasets. Non-missing values are the same across all datasets. The imputation produced five datasets, each with a distinct set of probable missing values. Finally, we obtained average regression coefficients and correct standard errors after doing multiple regression on each of the five datasets and pooling the results. As a result, we see a statistically significant influence of Chip rate on “YKappa” degree of delignification (Table 4 below). The active alkali charge in white liquor “UCZAA,” which has a negative estimate value of -0.525, is another predictor with the least p-value.

References
Gao, W., Zhou, L., Zhou, Y., Gao, H., & Liu, S. (2022). Monitoring the Kappa number of bleached pulps based on FT-Raman spectroscopy. Cellulose, 29(2), 1069-1080.
Marcelo, F., d’Angelo, J. V., Almeida, G. M., & Mingoti, S. A. (2018). Predicting Kappa number in a kraft pulp continuous digester: A comparison of forecasting methods. Brazilian Journal of Chemical Engineering, 35(3), 55-68.