Effects of Mass on the Braking Distance of a Bicycle Report

Research question

The aim of this experiment is to investigate the effects of mass on the breaking distance of a bicycle.

Hypothesis

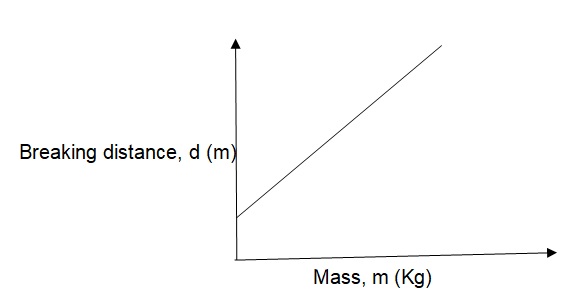
I believe as the mass of the bicycle increases so does the breaking distance. If we triple the mass of the load on the bicycle then the final breaking distance increases three times the initial distance. I am expecting this to happen since from Newton’s second law of motion the rate of impulse change is directly proportional to the external force acting on the body (Bueche 34). This external force which is the breaking force is commensurate to the product of mass and acceleration which eventually halts the body to a rest after a given distance d, and as such, work is done on the body. The work done is meant to counter the kinetic energy of the bicycle. The kinetic energy is factor of the mass and the velocity of the bicycle creating a direct proportionality between the mass of the bicycle and the breaking distance. Basing on the Newton’s 2^nd law of motion I think that if a graph is plotted of breaking distance against the mass then a straight line graph is expected portraying a direct proportion between the two variables (Bueche 34).

Mass, m (Kg)

Independent variable– mass, m (Kg)

Dependent variable- distance, d (m)

Controlled variables- acceleration of the body, a (m/s²)

• air resistance, A (N)
• slope of the surface, S (π^C)
• the coefficient of kinetic friction of the table, C (µ_f)
• gravitational acceleration, g (m/s²)
• length of the spring, l (m)
• spring constant, k (N/m)

Materials list

A sensitive spring that can accommodate a 500gm mass without undergoing deformation, meter rule, a free moving lab trolley, weightless thread (2 meters in length), masses (10×100gm slotted masses plus a 500gm mass), frictionless single pulley, a flat and smooth table (1 m in height), pan, tripod stand, two small wooden blocks, a small stool, four leveling wedges.

Diagram

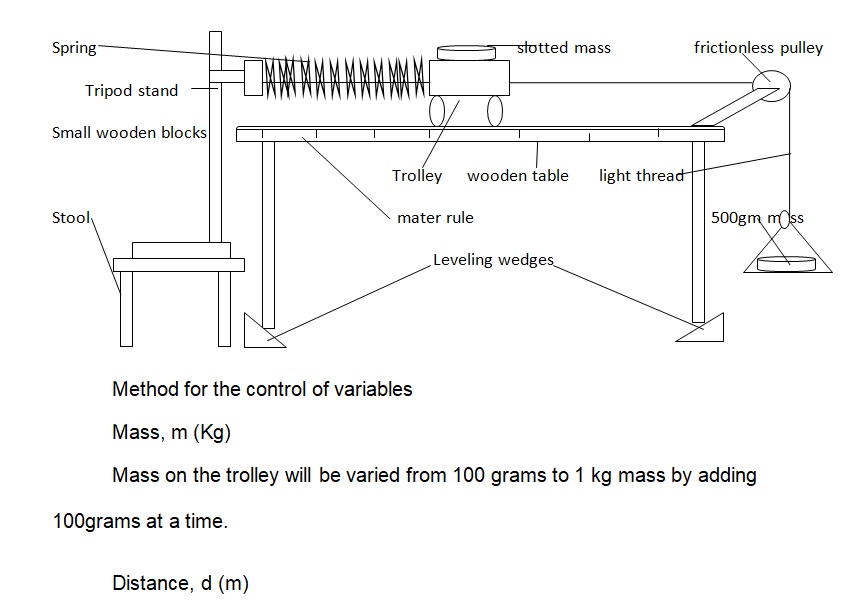
The breaking distance travelled by the trolley is measured by getting the difference between the final and the initial positions of the trolley using the meter rule. The initial mark is given by the actual length of the spring which has one of its edges (the one clumped on the tripod stand) coinciding with the zero centimeter mark of the meter rule. The final mark (obtained from the edge of the trolley on the side that is attached to the spring) is directly read on the meter rule after the trolley comes to rest. This procedure is repeated three times and then an average breaking distance is obtained.

Acceleration of the body, a (m/s²)

The acceleration of the body should be kept constant. This is obtained by maintaining the same mass on the pan hence the tension on the spring remains constant.

Air resistance, A (N)

This is controlled by carrying out the experiment in a closed laboratory room with the fans turned off. The experiment will be carried out on the same bench, position and on the same day to limit deviations due air resistance.

Slope of the surface, S (π^C)

The slope of the surface is kept constant at 0 π^C with the ground. This is done using a leveling wedge. This is tested by letting a trolley stand on the surface of the table to ensure it doesn’t move.

Coefficient of kinetic friction of the table, C (µ_f)

This is controlled by performing the experiment using the same table throughout at the same position, and using the same trolley all along.

Gravitational acceleration, g (m/s²)

Gravitational acceleration is controlled by performing the experiment in the same location until all the measurements are taken.

Length of the spring, L (m)

The length of the spring should be kept constant. This is controlled by using the same spring all along while checking to ascertain that it hasn’t undergone deformation by measuring its length every time before using.

The spring constant, k (N/m)

The spring constant should be maintained and this is achieved by using a similar spring all along.

Method for the collection of data

1. Set the apparatus as shown in the diagram above with one end of the spring clamped and coinciding with the zero mark of the meter rule (don’t attach the mass and the pan).
2. Attach the spring to the trolley and slightly pull the trolley to make it slightly taut, slowly release it to rest and record the actual length from the meter rule at the end of the trolley adjoining the spring (At this point the string with a loop at one end is attached to the trolley minus the hanging mass in a pan).
3. Add a 100 gm slotted mass on the trolley and then hang the 500 gm mass in a pan on the other end of the looped string.
4. Leave the trolley to come to rest and then record the final position of the trolley from the meter rule at the point where the spring adjoins the trolley.
5. Calculate the distance by finding the difference between the initial and the final mark.
6. Repeat the steps three times and then find the average breaking distance by dividing the summation of the breaking distances obtained by three after which you record the reading.
7. Repeat steps 1-6 for masses 200gms, 300gms in that order up to 1kg while recording your findings.

Table of mass on the trolley and the breaking distance

Data processing and presentation

The collected data is represented in a graph by plotting the values recorded from the table with the depended variable on the x-axis while the independent variable on the y-axis. This gives us a relationship between the two variables. Also included in the graph are the uncertainty bars in order to accommodate experimental errors.

Analysis of the graph

The data is analyzed using the equation; y= mx +c

Where by c represents the y-intercept i.e. the weight of the trolley

m-is the gradient of the slope

Investigation reveals that the breaking distance d, is related the mass m, of the body by the formula below: m = kd + c

Whereby k represents the gradient equivalent to 2F/V²

F is the tension on the string

V is the velocity of the trolley (Finck 28)

Evaluating procedures and results

1. The weights of the slotted masses were not weighed to ascertain their actual weight. They were assumed to be what their respective labels stated.
2. The parallax error was taken into account by placing the eye direct and perpendicularly above to the edge of the trolley.

Improving the investigation

To increase the precision of results in future then;

1. The slotted weights should be checked using an electronic digital weighing scale to ascertain their original weight.
2. The issue of parallax error could be minimized by mounting a pointer at the junction between the spring and the trolley.

Works cited

Bueche, Fredrick. Principles of physics, 3^rd edition.New York: McGraw Hill, 1997. Print.

Finck, Joseph, Forces and linear motion. Physics for ATHLETES and other serious students, 1^st edition, 2009. Web.