Introduction
Objective
It is necessary to investigate the issue and answer the question of whether energy is conserved in a simple mechanical system or not.
Procedure
The pendulum bob is suspended at a convenient length L. It is then held at height h which is recorded. The pendulum bob is released from the displaced height h and its velocity changes are observed and recorded as it swings back and forth.
Results
They are fully reflected on the data sheets provided.
Data analysis
The motion of a pendulum is a good demonstration of mechanical energy conservation. A pendulum consists of a mass (a bob) suspended by a string to a pivot point. The pendulum moves back and forth sweeping out a circular arc. The movement is done in a periodic fashion. There are only two forces influencing and acting upon the pendulum bob, they neglect air resistance which is very small even considering the small size of the pendulum. One of these forces is gravity which acts in a downward direction. It works on the pendulum bob and affects its motion. However, gravity is a conservative force, which is why it does not cause any change to the total mechanical energy of the bob.
Tension is another force that acts upon the bob. It is an external force and has the ability to change the total mechanical energy if it causes an influence on the pendulum bob. However, the tension force does not work because it acts in a perpendicular direction to the motion of the bob at any given time. Having no external forces that do the work, the total mechanical energy of the pendulum bob is therefore conserved. The conservation of mechanical energy is clearly seen where the falling motion of the bob goes with an increase in speed. As the bob loses height and PE, it gains speed and KE and thus, the total number of the two mechanical energy forms is conserved.
KE = ½ mv2
PEgravity = mgh
Total mechanical energy = K.E. + P.E.
Taking h = 0.1810m and v = 1.3810m/s
KE = ½ mv2
=½ m1.38102
=0.9535 J/kg
PEgravity = mgh
=m9.82*0.1810
=1.77742 J/kg
Total mechanical energy = K.E. + P.E.
= 0.9535+1.77742
= 2.7310 J/kg
Taking h = 0.1590m and v = 1.5320m/s
KE = ½ mv2
=½ m1.53202
=1.174 Jkg
PEgravity = mgh
=m9.82*0.1590
=1.560 J/kg
Total mechanical energy = K.E. + P.E.
= 1.174+1.560
= 2.733 J/kg
Thus, total mechanical energy in the system is conserved.
It is observed that KE appears to be at its maximum when h is at its lowest level. At the same point, PE is at its minimum when KE is at its minimum as well. It happens when h is at the highest level. In this very case, PE is at its maximum. Therefore, taking into account and operating with doubtful and inaccurate data of h, a person cannot expect to get correct results because they will be changed, so we will have maximum KE at the highest value of h.
Discussion
Considering the figure shown below, we get the following data.
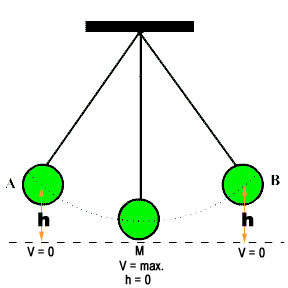
At point ‘A’, velocity of the bob is zero. Therefore, K.E. at point ‘A’ = 0.
Since the bob of the simple pendulum is at a height (h), therefore, P.E. of the bob will be maximum at this point. i.e.
P.E. = mgh.
Total energy = K.E. + P.E.
= 0 + mgh = mgh
Thus, at point A, the total energy is potential energy.
When the bob of pendulum is released from point ‘A’, the velocity of bob increases gradually, while the height of bob is decreasing accordingly to it. At point ‘M’, velocity will become maximum and the height will be equal to zero. Therefore, from the equation below, it is seen that kinetic energy can be calculated. The total energy is a result of the summing of the given scores of two energies. Kinetic energy plus potential energy is equal to the total energy.
K.E. = maximum = 1/2mV2, but P.E. = 0.
Total energy = K.E. + P.E
= 1/2mV2 + 0
= 1/2mV2
Hence, in this case, P.E. is completely converted into K.E. at point ‘M’.
At point M, the bob of the pendulum does not stop due to inertia. It moves towards the point ‘B’ with its velocity gradually decreasing while on the contrary, the height increases. At point ‘B’, velocity of the bob becomes zero.
Thus, K.E. at point ‘B’ = 0, but P.E. = max.
P.E. = mgh.
Total energy = K.E. + P.E.
= 0 + mgh
= mgh
Thus, at point B, total energy is again potential energy.
The measurements which are recorded in the datasheet are consistent with the equations that are shown above. The graphs drawn on the data sheets clearly show the law of conservation of energy which states that energy is never created nor destroyed. But, on the contrary, it is only changed from one form to another. We observe how PE converts to KE immediately when the pendulum bob is released from rest. Also when h is at lowest point and KE is at its maximum, we observe KE that is converted to PE now.
Abstract
In any experimental exercise that deals with such a case, some statistical and systematic errors may occur. However, it is considered to be an experiment, that is why it is not exempted from errors. For this study, statistical errors that may affect or influence the accuracy of the measurements include errors because of the equipment used to take the measurements. For example, the discrepancy may occur because of meter rules or timer. The failures may happen also when the readings are expressed to given decimal places or significant figures. However, these errors can be ignored or assumed.
Systematic errors lead to biased results. In this experiment, it is assumed that air resistance is negligible, thus, there is no friction which may lower the acceleration of the pendulum bob. Also controversy and inaccuracy in the pulleys which are assumed frictionless in the formula bring about biased results. These factors introduce systematic errors in the measurements which are taken in the experiment. Some of the inaccurate data can be ignored or seen as assumptions.
Conclusion
In conclusion, from the above analysis, it is observed that the total energy during the motion does not change, but is constant. This means that the motion of the bob of simple pendulum is in line with the law of conservation of the energy. Hence, the objective of the lab experiment which was to investigate the conservation of energy in a simple mechanical system is met. However, some errors might have produced some biases.