Introduction
The experiment aims at establishing KHT molar solubility in MgSO4, Glucose, HCL, and H20. The test will also ascertain existing variations in the effects as related to other ions. Equilibrium expression is a vital instrument that can be used to illustrate the solubility of a variety of electrolytes. This experiment will attempt to establish the exact solubility of Potassium Bitartrate, which is connoted by [K+] [HT–] dissolution as presented in equation 1 below.
Equation 1; KHT (s) ⇄K+(aq) + HT– (aq)
As summarized in equation 1, equilibrium expectorate is the reciprocal of products over reactants with the exclusion of solids and liquids as a constant value (K). As discussed in the Le Chatelier’s Principle, the liquids and solids, connoted by K, are not considered. Based on this principle, the final equation for equilibrium expression for Potassium Bitartrate in this experiment is KHT = [K+] [HT–]. The KHT is excluded for the reason that it is solid in the physical state. Therefore, if the results of the experiment established that the constant K is greater than 1 (K>1), it is an indication that the mixture is made up mostly of solubility products. On the other hand, if the constant K is less than 1 (K<1), it will indicate that the mixture is made up mostly of reactants. The experiment will also involve the calculation of the solubility product constants denoted by Ksp of KHT. Ksp is the product of dissolved ions saturation as a fraction of their coefficients. Thus, the calculated molarity of NaOH is used to compute the molar solubility of KHT, which is the quantity of KHT moles that are liquefied in every liter before saturation level.
As illustrated in Le Chatlier’s Principle, the addition of reactants results in a reaction that favors the product side. On the other hand, the addition of products would lead to a reaction that favors the reactant’s side. In contrast, a subtraction on either side, that is, products and reactants would give a different result. This is summarized in equation 2 below.
Equation 2; KHT (s) ⇄ K+(aq) + HT– (aq)
From the above equation, it is apparent that any addition of KHT would not result in changes in the product’s side because of its physical solid nature. It is also insoluble at the point of solution saturation.
In the course of the experiment, titration will be used to determine the unknown solution concentration (acid) from a known solution (base). The right quantity of the unknown solution will be measured using a burette frequently to the point of complete reaction. Phenolphthalein indicator will be used to confirm completion of the reaction at the point where the solutions change color to light pink. After collecting all the values when the reaction is completed, the next step is to calculate solubility products constant and molarity solubility of KHT. Since the NaOH concentration is known, it is measured in milliliters (MLS) in terms of the quantity required to completely neutralize the unknown solution. The MLS was then converted to liters (l) and multiplied by the known concentration to compute the added moles. The next step is converting the NaOH moles into KHT moles since they have a similar ratio of 1:1. Equation three below highlights the similarity in the ratio of NaOH and KHT moles.
Equation 3; HT–+ HO–⇄H2O + T-2
The KHT moles were then divided by 25ml of the solution containing dissolved KHT to establish its molar solubility as summarized in equation 4.
Equation 4
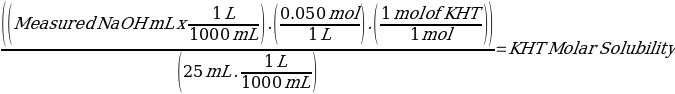
Computing Ksp was done by getting the product of KHT average Molar Solubility for each trial and itself since the Ksp constant of KHT is equal to its concentration at ratio 1:1 as explained in equation five below.
Equation 5; KHT (s) ⇄ K+(aq) + HT– (aq)
Ksp = [K+] [HT–] = [KHT]2
A strong base (NaOH) was used to titrate the solutions since anion (HT–) is a relatively weak acid. This step is followed by dissolving KHT with 0.05M of MgSO4, water, and 0.025M of MgSO4. As captured in table 1, the findings were recorded for each trial.
Procedure
The first step involved filling three Erlenmeyer flasks. The first flask was filled with 200ml of 0.05 MgSO4 and 100ml of water to halve the concentration to 0.025 M. The second flask was filled with 200ml of water and the last was filled with 200ml 0.05 M MgSO4. This was followed by adding a gram of KHT in each flask and stirring for about 20 minutes using the magnetic stirrer. The third step involved pipetting 25.00ml of each solution in the three flasks into three beakers. The fourth step was adding three drop Phenolphthalein in each of the three beakers. The last step was a titration of each beaker with a NaOH-filled burette and volumes required to change the color of solutions in each beaker to light pink noted. The steps were repeated for two trials for each solution.
Results
The results of the two trials for each of the three solutions are summarized in table 1 below.
Table 1. Experiment results.
Discussion
The experiment aimed at establishing the variances in KHT molar solubility in Glucose, MgSO4, and water. The results indicate that the highest milliliters of NaOH are required to turn the MgSO4 solution to light pink as compared to other solutions. This reveals that there are no common ions between MgSO4 and KHT. In the KCI solution, it takes half the MLS of NaOH that is taken up in the water solution to change the color to light pink. A reasonable explanation could be that there are many common ions between KHT and KCI, thus the little MLS of NaOH was taken up. There was negligible variation in the NaOH quantity used for water and glucose solutions. Another interesting finding was that increased KCI concentration resulted in increased usage of NaOH due to a rise in common ions. The same scenario occurred when the concentration of MgSO4 was increased.
The findings confirmed the literature review which indicated that adding Kor HT or would give a different result for each solution because of its aqueous nature and being on the product side. As observed, it shifted the chemical reaction to the reactant’s side. In the case of substance subtraction, that is, removing KHT from the solutions, there would be no shifts in the reactants side. However, subtraction of Kor HT on the side of products resulted in a shifting reaction on the right side to adjust the equilibrium. The highest quantity of base (NaOH) was used in the solution with MgSO4 simply because of the existence of negligible common ions. To provide accurate readings, air bubbles from the burette were removed to minimize error in the measurement of NaOH usage is recorded. Another source of error is contamination in the equipment in the preceding trials. This was avoided through the proper rinsing of the experiment instruments.