Abstract
The objective of this experiment was to determine the nature and the phase differences between voltage and current for reactive components in a series LRC resonant circuit.
In this experiment, a series LRC circuit was connected using a resistance (R= 20Ω), capacitor (C= 10μF), and load (L= 85mH). An AC. current with a frequency of 100Hz and an amplitude of 2 volts was fed into the circuit as an input signal. The frequency of the original waveform was adjusted to produce a waveform twice big. Voltages across each component were determined then fed to a graphical analysis to reveal the trends of the waveforms.
From the graphical analysis, as opposed to an inductor, it was revealed that the capacitor gave a consistent result i.e. the current led the voltage (Storr 9). The phase differences for both waveforms were <π/2 i.e. -17/35π and 19/35π for the capacitor and inductor respectively. The inconsistency concerning the inductor could be due to fluctuations in the input current.
Objective
The objective of this experiment was to determine the nature and the phase differences between voltage and current for reactive components in a series LRC resonant circuit.
Procedure
A series LRC circuit was connected using a resistance (R= 20Ω), capacitor (C= 10μF), and load (L= 85mH). An AC. current with a frequency of 100Hz and an amplitude of 2 volts was fed into the circuit as an input signal (scope channel number 1). Significantly, this input signal was set to display both voltage and current signals concurrently such that there was no existence of phase difference. Later, the frequency was set such that the output signal (scope channel number 2) of the load was half the original with the aim being; to compare its nature with the previous signal. Using a digital voltmeter (DVM), the voltages around each component were recorded for analysis. The waveforms v (t), for each component, was digitized to obtain data that was fed into the graphical analysis to reveal their trends.
Experimental data
Table 1: of the voltages across each component.
Table 2: of the maximum/minimum voltages across each component per given time.
Table 3: of resistor waveform.
Table 4: of inductor waveform.
Table 5: of SG waveform.
Table 6: of capacitor waveform.
Table 7: of phase angles and reactance of the components.
Graph of voltages against time portraying phase shift.
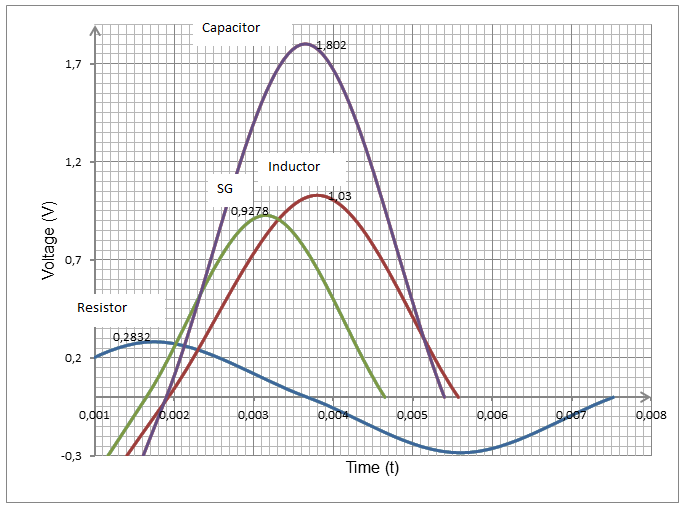
Results
To obtain the resonant frequency, the formula below is applied:
ω0 = 1/ (LR) ^0.5.
But, ω0 = 2πf0
Therefore, substituting for ω0 in the first equation and consequently making f0 the subject matter we obtain: f0 = 1/ [2π*(LR) ^0.5.
Hence, f0 =1/ [2π*(8.5*10 ^-2 x 10 ^-5)
= 1.8 x 10 ^5 Hz.
=1.8 x 10 ^2 ± ׀error׀ KHz.
׀error׀ is obtained from the expression: Δf0 = Δω0/2π where Δf0 is equivalent to the absolute error. But, Δω0 = ω0 [(ΔL/2L) ^2 + (ΔC/2C) ^2] ^0.5, ΔL/L= 0.05 and ΔC/C = 0.01
Therefore,
Δ ω0 = 8.5*10^-2(0.025^2+0.005^2) = 5.525x 10^-5.
Hence, ׀error׀ =±8.6 x 10^-5Hz = ±8.6 x 10^-8 KHz.
Therefore, the calculated value of resonant frequency f0 = 1.8 x 10^2 ± 0.0086E^-5 KHz.
The phase angles as represented in the table 7 above were obtained as is in the calculation below:
Phase angle (Φ) for the general signal (SG) = 2πΔt/T
= 2π (0.0047-0.0037)/ 0.007
= 2/7π radians.
Phase angle for capacitor = 2π (0.0054-0.0037)/ 0.007 = 17/35π radians.
Phase angle for inductor =2π (0.0056-0.0037)/ 0.007 = 19/35π radians.
Reactance for the components are obtained as is in the calculation below:
Reactance for inductor (XL) = 2πfL
= 2π*100*85×10^-3 = 53.4 Ω
Capacitance reactance (Xc) = 1/ 2πfC
= 1/ (2π*100*10×10^-6) =159.1 Ω
Circuit impendence (Z) = [R2+ (XL-XC) 2] ^0.5
= [20 ^2+ (53.4-159.1) ^2] ^0.5 = 107.58 Ω
The current flowing through the circuit is obtained from the calculation below: I =Im/√2.
But, Im as obtained from the graph above is equivalent to 0.2832V.
Therefore; I =0.2832/√2 = 0.2 A.
Hence, the voltage across each component is calculated as is below:
The voltage across resistor (VR) = IR = 0.2*20 = 4V.
The voltage across the capacitor (VC) = 0.2*159.1 = 31.82V.
The voltage across the inductor (VL) = 0.2*53.4 = 10.68V.
The voltage input across the circuit (Vi) = 0.2*107.58 = 21.52V.
The sum of these values of voltages does not sum up to zero i.e. 4+31.82+10.68+-21.52 ≠ 0.
Discussion and analysis
The objective of carrying out this experiment was to determine both the nature and the phase differences between the current and the voltage for reactive components in an LRC series circuit (Storr 9). The components under investigation as portrayed by the graph above were a capacitor and an inductor. Just as expected for the capacitor, as exhibited by the graph above, the nature was such that the current lead the voltage. This behavior is owed to the fact that the voltage between capacitor plates is directly proportional to the charge density. As such, the current, which by definition is the rate of flow of electric charge, is responsible for delivering charge to the capacitor plate first before the voltage is raised.
As for the inductor, theoretically, this is supposed to be the opposite of the capacitor’s behavior. As such, the current ought to lag behind the voltage. Principally, an inductor impedes a change in current hence; it builds at a decreased rate lagging behind in time and phase. However, for this experiment, the opposite happened. This can be attributed to experimental uncertainty in the course of the experiment (Storr 9).
The components exhibited phase differences concerning the current which is the waveform synonymous to that displayed by the resistor and superimposes its voltage waveform. Thus, for the resistor the phase difference is null. For the other components i.e. the capacitor and the inductor, the phase differences are -17/35π and 19/35π respectively. The negative sign is significant in revealing the position concerning the current. Its presence reveals the identity of the component as a capacitor. The opposite is true for an inductor (Storr 9).
Concerning the voltage across each component, and since this circuit is closed it was expected that the algebraic sum of these voltages would be null (according to Kirchhoff’s law). Nonetheless, on summing up, the total defies this law. This could be attributed to disparity accrued in the course of the experiment. This could be among other fluctuations in the input signal which might interfere with the output signals. This can be mitigated by appropriately connecting a capacitor in parallel to store charge. However, this should not interfere with the circuit.
Conclusion
The objective of this experiment was to determine the nature and the phase differences between voltage and current for reactive components in a series LRC resonant circuit. This was partially achieved since it was ascertained that the current leads the voltage for a capacitor. With regards to the inductor, experimental errors hampered the acquisition of consistent results. Also, it was established that the phase differences for the capacitor and the inductor, were -17/35π and 19/35π respectively.
Work Cited
Storr, Wayne. Basic electronics tutorials. Web The Series LRC Circuit. 2012. Web.