Magnetic Fields: Charge-to-Mass Ratio of an Electron Report

Abstract

The main objective for performing this experiment was to investigate the e/m ratio of an electron. This was achieved courtesy of an electron gun embedded within an evacuated glass bulb surrounded by a pair of Helmholtz coil. After allowing at least 5 minutes of cathode heating, for the first approach, the current (I) was varied at a constant voltage (300V) to vary electron radius (R). These were then recorded for analysis where a graph of β (magnetic field) against 1/R was plotted to determine e/m. For the second approach though, while keeping everything intact the voltage (V) was varied at a constant current (1.5A). A graph of V against R² was plotted just the first approach to determine e/m. These values were then compared with the theoretical value (1.76×10^11 C/Kg) to ascertain them.

From the analysis, the first approach gave a ratio of 2.4×10^11C/Kg which translates to a 36% error. For the second approach though, the graph gave a ratio of 1.63×10^11 C/Kg equivalent to 7.38%. As such the best approach in future experiments is the second one. The errors experienced in the course of the experiment have a bearing on the ambient magnetic field due to Earth’s poles. This can be decimated in future by “orienting the apparatus fields in line with the Earth’s but in the opposite direction” (Becker 10).

Objective

The object of this experiment was to determine the charge to mass ratio of an electron courtesy of an electron gun.

Procedure

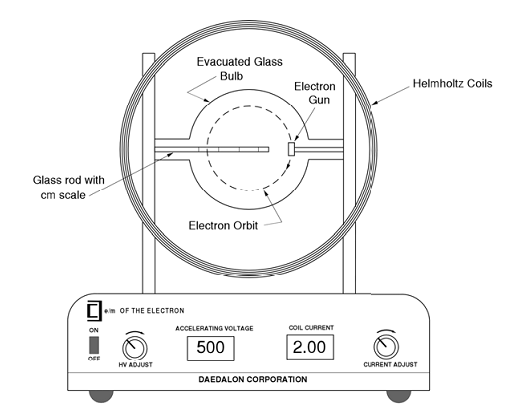
In this experiment, two consecutive procedures were used though using the same equipment. In the first procedure, a heated electron gun at 300V potential difference and, embedded within one end of an evacuated glass bulb was fixed between a pair of Helmholtz coil (having turns, N, equivalent to 132. See fig 1). The electron gun was allowed to heat for at least 5 minutes before the commencement of datum acquisition. Meanwhile the average diameters for both coils at different axes, both internally and externally were averaged to determine the radius, a, vital for analysis. For the sake of urgency in calculation of β (applied magnetic field of Helmholtz coil), the coefficient of the current, I, was determined.

At least 5 minutes after connection a greenish straight beam was seen hitting on the other end. The current (I) of the coil was adjusted to bend the beam to a diameter of 11 cm. The same was done for several diameters from 11 and 5 cm. at 1 cm. interval while at the same time recording the current and the diameter correspondingly. Reversely, the same was done from 5 to 11 cm. and as such a corresponding datum was obtained to determine average values. To eliminate uncertainty as regards secondary magnetic field the entire orientation was turned at 180° and the procedure repeated. The mean values from the two orientations were averaged for analysis. As such, a graph of β against 1/r was plotted to determine e/m (electron charge-mass ratio).

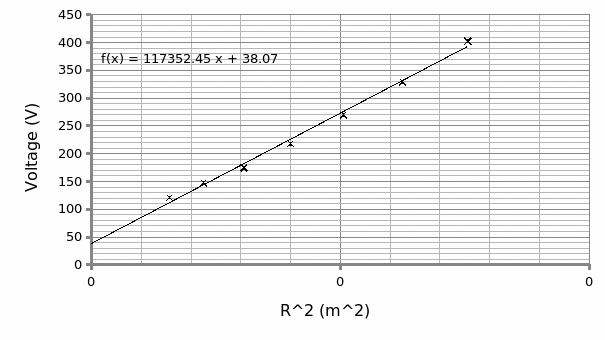
Akin to the first setup was the second experiment however; the accelerating voltage (V) was the variant while holding the current constant at 1.5A. A graph of V against r^2 was plotted for this case to determine e/m for comparison to the first setup and the theoretical one.

Experimental data

Table 1: of the average diameter (a).

Table 2: of varying current at 300V (Part 1).

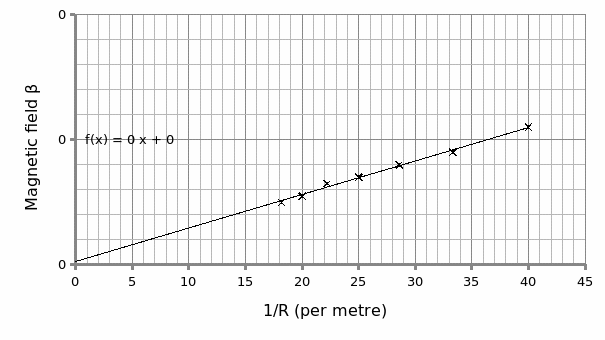
Table 3: of varying voltage at 1.5A (Part 2).

Results

From Table 1, the distance (a) to the center of the coil is obtained as below: a= (0.31+0.309+0.286+0.285)/4=0.14875m.

The average current (I) is obtained from the expression:

• I_avrg= (I₀1+I₀2+I₁₈₀3+I₁₈₀4)/4
• = (1.22+1.22+1.3+1.3)/4
• =1.265A.

The magnetic field (β) is obtained from the expression:

β= (μ₀NI/a) (4/5) ^3/2

Where:

• μ₀= 4π × 10-7 T·m/A (permeability constant),
• N=132 (number of turns of Helmholtz coil),
• a= 0.14875m and, the current is given by I.

Therefore for the first value at 1.265A (Table 2):

β = (4π*10^-7*1.265*132/0.14875) (4/5) ^3/2

=0.0010 T.m/A

Graph 1 is plotted from the expression:

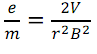
As such on rearranging the equation we get: β=1/r (2mV/e) ^1/2

Therefore on plotting β against 1/r the gradient (S) = 5×10^-5 = (2mV/e) ^1/2.

Hence, m/e=(S^2)/2V

= (5×10^-5) ^2/ (2*300)

= 4.17×10^-12 Kg/C

Then, the reciprocal of m/e gives us e/m:

m/e =1/ (4.17×10^-12)

= 2.4×10^11C/Kg.

For part 2 the average voltage (V) is obtained from the expression:

V_avrg= (V₀1+V₀2+V₁₈₀3+V₁₈₀4)/4

Therefore:

V_avrg= (424+420+382+384)/4

=402.5V.

As regards to Graph 2, the expression below as derived from the expression above is vital in the determination of the e/m:

V= [(eβ^2)/2m)*r^2

Therefore plotting V against r^2 gives the slope (P) as (eβ^2)/2m) = 11735 Vm^2.

Hence:

e/m= 2*11735/β^2

But at I = 1.5A, β = (4π*10^-7*1.5*132/0.14875) (4/5) ^3/2 = 1.2×10^-3 T.m/A.

Therefore:

e/m=2*11735/ (1.2×10^-3) ^2

= 1.63×10^11 C/Kg.

The actual charge per unit mass is approximately 1.76×10^11 C/Kg. Hence, the error as obtained from the first part is given by:

[(2.4-1.76)*10^11]/1.76×10^11*100%

= 36%

For the second part though the error was small i.e. [(1.76-1.63)*10^11]/1.76×10^11*100%

=7.38%

Discussion and analysis

This experiment was set with an objective of investigating the charge to mass ratio of an electron using two different approaches and as such, the values obtained confirmed by the theoretical one. The first part of the experiment gave this ratio as 2.4×10^11C/Kg thus, with respect to the theoretical value (1.76×10^11 C/Kg), an error of 36% was registered. This, results with respect to the second approach gave a bigger margin of error. This is so because the second part of the experiment which gave a ratio of 1.63×10^11 C/Kg, registered an error of 7.38%. Thus, in future experiments the second approach is the recommended one. These errors though have a bearing on the ambient magnetic field due to the Earth’s poles. The Earth’s magnetic field “is approximated to be 0.1mT and pointing into the ground at an angle of 58° relative to the horizontal” (Becker 9). As such, to decimate the effects of the Earth’s field then the apparatus should be aligned such that its fields is concordant with the Earth’s though in opposite directions.

In addition, in order for this experiment to be a success in the future then proper location of the venue should be considered. This would definitely form a fascinating subject worthy to be studied in another day.

Conclusion

In a conclusion, the objective of the experiment was met since we were able to estimate the e/m ratio using different approaches that gave consistent results with the theoretical value (1.76×10^11 C/Kg).

Works Cited

Becker, Joseph. Physics 51-Electricity and Magnetism. Carlifornia: San Jose State University Press, 2003. Print.

Serway, Raymond. Physics for Scientists and Engineers with Modern Physics. Denver: MacMurray, 1996. Print.