Introduction
Optimization is the keyword in the economy as everybody wants to utilize the minimum possible resources to derive maximum possible functionalities. This is quite natural considering the fact that resources are limited and the needs to be fulfilled are unlimited, so the only choice is to go for optimization. Optimization means getting maximum possible output from the minimum possible inputs.
Fortunately, mathematics proves to be a great help, whenever and wherever one has to deal with the terms like optimization, maxima, minima etc. Two branches of mathematics – algebra and/or calculus prove very handy in solving the problems related to optimization, maxima, minima etc. In this case, the cross-section of a gutter will be optimized to contain maximum water with a minimum of the material of construction.
Problem Statement
A gutter is to be made of plastic to catch water at the edge of a roof. Naturally, the manufactures would like to have a design of a gutter that holds maximum of water with a given amount of material required to fabricate the gutter. Now the problem is what should be the shape of the cross section of the gutter.
Three possible shapes are suggested

Referring to the figures above, it is easy to understand that the shapes are made of the black lines i.e. black lines represent the length of the material required and water is contained in the cross-sectional area of these shapes i.e. the shaded area. The problem is to find out the optimum cross-sectional area which requires minimum of the construction material (plastic) as it is the cross-sectional area that holds water.
Solution
This is a problem of maxima and minima. Looking at the suggested cross – sections the problem reduces to minimizing the periphery of the gutter cross-section for a given area of the cross-section, this is because, while the periphery is made of the construction material (here plastic) the cross-section holds the water.
Analytical Solution
Let us assume that the length of material (here plastic) is ‘l’ and this is folded to make different cross-sections for the gutter with area ‘A’. Now for a given area ‘A’, the length of the material ‘l’ should be minimized or for a given length of the material ‘l’, the cross-sectional area ‘A’ should be maximum. In this analysis, four shapes will be considered – Triangular cross-section, Rectangular Cross-section, Semicircular cross-section and circular cross-section.
Triangular Cross-Section
Let us assume that the material of length ‘l’ is folded to make a triangular cross-section with area ‘A’ and included angle ‘θ’.
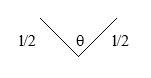
Area of a triangle is given by
A = (1/2)*(length of one side)*(length of adjacent side) Sinθ
Where θ is the angle included between these two sides
In this case, length of the two sides together is l, there fore length of the either side should be equal and should be equal to l/2 for maximizing the area.
Therefore, cross-sectional area of the triangular gutter will be A = (1/2)*(l/2)*(l/2)*Sinθ (Refer figure, above)
For A to be maximum for a given ‘l’, Sinθ should be maximum and its maximum value is 1. Therefore, the maximum possible value of area ‘A’ will be A = (1/8)l2
For Rectangular Cross-Section
Let us assume that height of the rectangular gutter is ‘x’, then length of the gutter will be l-2x. For a rectangle Area A = length * breadth
Therefore, for a rectangular gutter
A = x*(l-2x) = lx – 2x2 (refer the figure below)
l – 2x If x is increased then l-2x will decrease and vice-versa, as l is fixed leading to decrease in area of the cross-section of the gutter. Therefore, for the cross-sectional area of the gutter to be maximum there has to be a definite relationship between l and x. This is determined by differential calculus applying the derivative of area with x.
For, A to be maximum or minimum ![]()
Therefore, maximum area of the rectangular gutter will be, A = (1/8)l2
Semi-Circular Cross-Section
Radius will be r = l/π and
Areas will be A = (1/2)πr2 = (1/2π)l2 = (1/6.28)l2 (refer the figure, below)
Radius will be r = l/(2p) and
Areas will be A = πr2 = (1/4π)l2 = (1/12.56)l2 (refer the figure on the next page)
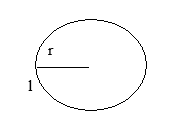
These values are presented in the form of a table in Table 1 for the sake of comparison.
Table 1: Area of a cross-section of gutter with a given periphery ‘l’.
Numerical Illustration
For better comprehension of the subject, let us use some numerical illustrations. Let us take a material of 1 m length and fold it in different forms and let us see how the area of cross-section of the gutter is changing with shape.
Length of the material l = 1 m.
Thus it can be seen that if a material of same length is folded into different kinds of shapes, the semicircular shape provides the maximum cross-sectional area. Maximizing of the cross-sectional area of the gutter is important as this gives the maximum amount of water a gutter can take into it. Therefore, it can be concluded that so minimized the quantity and therefore, the cost of the material, the ideal shape of the gutter will be semi-circular.
Conclusions
Based on the analysis of the problem it can be concluded that the gutter should have a semi-circular cross-section to minimizes the use of construction material.