Physics: Permeability of Free Space Report

Introduction

In the lab session, the repulsive magnetic force between two wires with antiparallel currents was balanced by a known gravitational force. The result obtained from the lab session was used to calculate an experimental value for the permeability of free space µ_o (Lehn 1151).

Special Concerns for the Lab

The lab required extremely careful manipulation of the sensitive balancing information. Excessive movement in the Lab room was thus discouraged. The currents were left ON for 60 seconds or less since the large currents used in the current balancing experiment could cause excessive heating. Additionally, the output signal was always brought to a minimum first before turning the power supply off or on, by rotating the voltage adjusting the knob counterclockwise to the end position.

Objectives

• To determine an experimental value of the permeability of free space µ_o
• To investigate the balancing of repulsive magnetic between two wires with antiparallel currents by using a known gravitational force

Theory/Literature Review

The setup for the current balancing experiment can be shown in figure 1 below.

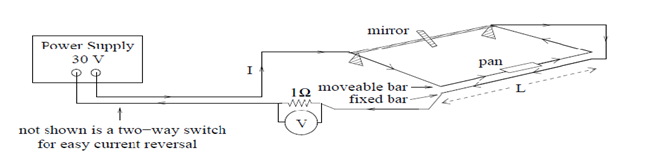
The current I can be passed in opposite directions through the horizontal bars. The lower bar can be fixed in place, and the upper bar is movable and can be brought to a few millimeters of the fixed bar using an adjustable counterweight. The gap between the bars can be measured by an optical lever and should be set to be approximately 2.0mm with the current off.

A set of masses are attached to the upper bar. The current I can be slowly increased until the movable bar returns to its initial position to compensate for the added weight. At the time the repulsive magnetic force is approximately equal to the weight of the added mass. The measured magnetic force can be equated with the calculated magnetic force F_B using the relationship:

F_B= µ_oLI²/2πr

Where L was the length over which the currents were antiparallel and r represents the separation distance between the two currents.

Equipment

• Power Supply 30V
• 1Ω resistor
• Voltmeter
• Fixed bar movable bar
• Pan mirror
• Connecting wires
• Ruler
• Optical lever

Procedure

Masses were added to the pan starting with 20mg ad going to 120mg in units of 20mg. For each mass, I was adjusted so that the upper bar could return to its equilibrium position. M and I were recorded. The masses were removed in units of 20mg, recording m and the necessary I for equilibrium. When all the masses were removed, the equilibrium position was checked not to have changed by the action of adding and removing masses.

The results were affected by the magnetic field of the earth. To reduce the effect, a two-way knife-edge switch was used to reverse the current direction and the entire steps above were repeated. The value of µ_o for each experiment was calculated and the average for the two values was computed.

To determine the values of µ_o from the two experiments, a graph of I² versus mg was drawn, first for the forward current direction, and again for the reverse current direction. Two values of µ_o were determined from the slopes of the graphs. The average of the two values was computed to get the final experimental value for µ_o. The measured µ_o values were then compared to the value defined by 4π x 10^-7 N/A².

Results

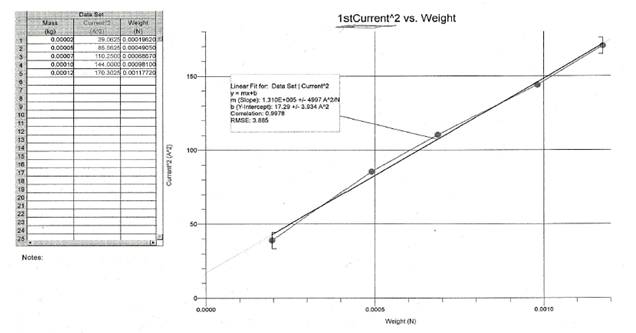
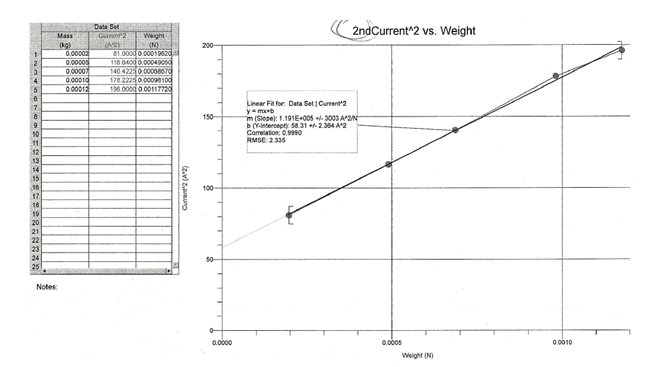
Discussion and analysis

The measured currents were used the experimental value of µ_o instead of comparing the forces directly. A comparison with the defined value of µ_o by 4π x 10^-7 N/A² was then made. The distance r between the currents was determined with an optical lever.

An observer experimenting could look through the mirror, and thus, by reflection, at the same point on the ruler. By recording two observed ruler locations, x_t when the two bars are touching and x_eq when the upper bar is in its equilibrium position. The distance r was then calculated as:

Where 3.18 mm was the diameter for each bar

The equation above can be explained with the aid of two figures as shown below. Figure 3 below shows the mirror position and a reflected light ray when the bars are touching. Ø is the angle of reflection or incidence for the reflected light ray. The center to center distance between the bars is 3.18 mm when the bars are touching. The distance is r at the equilibrium position.

Figure 4 below shows the mirror position and the reflected light lay when the upper bar is at its equilibrium. Since the mirror was tilted by an angle Ɵ about its initial position, the scope does not move, and the angles of incidence and reflection both reduce by Ɵ. The original light ray from x_t was as drawn in figure 4. The angle between the two rays, one from x_t and the other from x_eq is 2Ɵ.

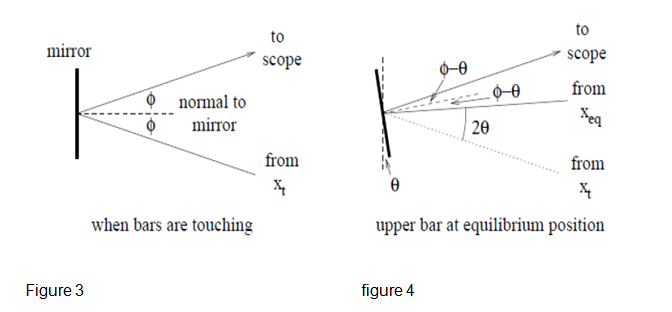
The calculation for r relies on the fact that 2Ɵ is a small angle, such that the difference between a triangle containing the angle 2Ɵ and a piece of the circle containing the small angle can be ignored. Hence, for Ɵ in radians:

Eliminating Ɵ and solving for r yields the equation above.

Finally, a few preliminary measurements were made before the start of the experiment. The measurements included the value a, which denotes length of the upper arm of the optical and was 21.75 cm. Also, the value of L, denoting the effective length of parallel bars was measured as 26.50 cm. The value of r can then be calculated from these results (Lehn 1155).

Conclusion

The lab session was carried out successfully. The main objectives for the experiment were met. The major objectives included determining an experimental value of the permeability of free space µ_o and investigating the balancing of repulsive magnetic between two wires with antiparallel currents by using a known gravitational force.

Additionally, special cautions were followed during the lab session. The special concerns included the lab requiring extremely careful manipulation of the sensitive balancing information. Excessive movement in the Lab room was also discouraged.

The currents were left ON for 60 seconds or less since the large currents used in the current balancing experiment could cause excessive heating. In addition, the output signal was always brought to a minimum first before turning the power supply off or on, by rotating the voltage adjusting the knob counterclockwise to the end position.

Works Cited

Lehn, Sonnenmoser. “Line Current Balancing with a Unified Power Flow Controller.” IEEE Transactions on Power Delivery (2009): 1151-58. Document.