Crime is a geographically dispersed social problem with economic implications on people and nations (Wolf, Gray, and Fazel 2). However, a causal relationship between crime and poverty is not obvious because crime can affect either the affluent or the poor in society. This leads to the question of if a correlation exists between poverty and crime. This is because crime rates in many countries such as the USA have reduced significantly between 2000 and 2008. Examples include states such as Minneapolis, with a 47% decrease, 31% for New York, 39% for Seattle, and 17% for Los Angele (Sudbury 3).
However, poverty causes certain stress among different people which results in individuals committing a poverty-related crime (Jones 2). While the statistics fail to positively correlate crime with poverty, other studies elsewhere affirm otherwise. This is evident in the period between 2009 and 2012, which shows a positive correlation between poverty and crime (Townsend 8). The goal of this study is to establish whether there is a positive correlation between poverty and crime (Bradshaw 8). The topic of discussion is important because it is not only interesting but provides an explanation that links poverty with the crime.
We used data from 40 countries that were hosted on two websites which shows the crime index and the percentage of people living below the poverty line. The data was analyzed using both SPSS and excel spreadsheets. Typically, there was no data collected on other variables that could affect the poverty index in the countries.
The first step was to run the data on SPSS and generate the descriptive statistics showing that data was taken from 40 countries. As shown in table 1, the minimum percentage of people living below the poverty line is 7.90% and the maximum value is 80% in the countries of interest. The mean and standard deviations are 30.4100 and 14.90599 respectively. The minimum value for Crime Index is 22 and the maximum value is 84 while the mean is 53.74 and the standard deviation 14.884. In both cases, the standard deviations show that the results are widely dispersed from the mean. This implies that there is a state of unequal difference because of different factors underlying crime in different countries.
Statistic test
Table 1.
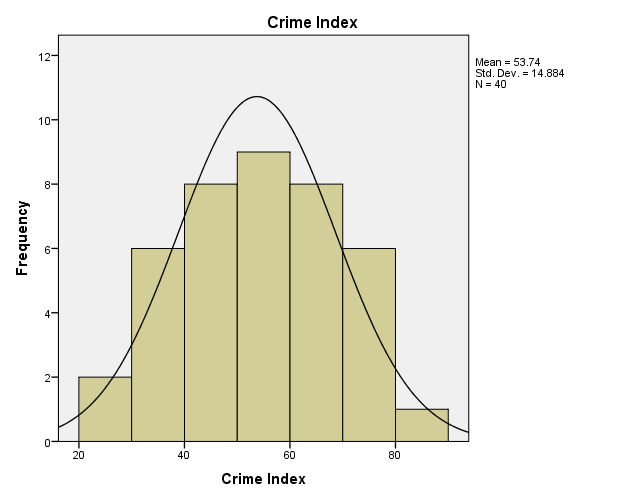
The histogram in figure 1 shows that the variable, crime index is fairly distributed with a normal bell-shaped curve. This shows that crime across the countries is normally distributed with a mean of 5374 and a standard deviation of 14.884.
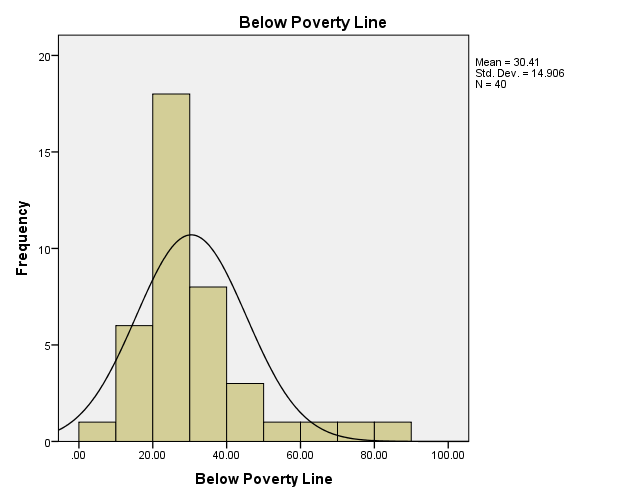
On the other hand, the curve in figure 2 is not symmetrical about the y-axis and the mean, which indicates that crime is not equally distributed across the countries that were investigated for the relationship between poverty and crime.
To determine the correlation coefficient between the crime index and the people living below the poverty line, a correlational study was run on a 2-tailed test at a 0.01 significance test and the results showed a Pearson Correlation coefficient of.427 **. This shows that the strength of the relationship between the crime index and people living below the line of poverty is.427. Despite the relationship is positive, it is evident that the relationship is weak.
Table 2.
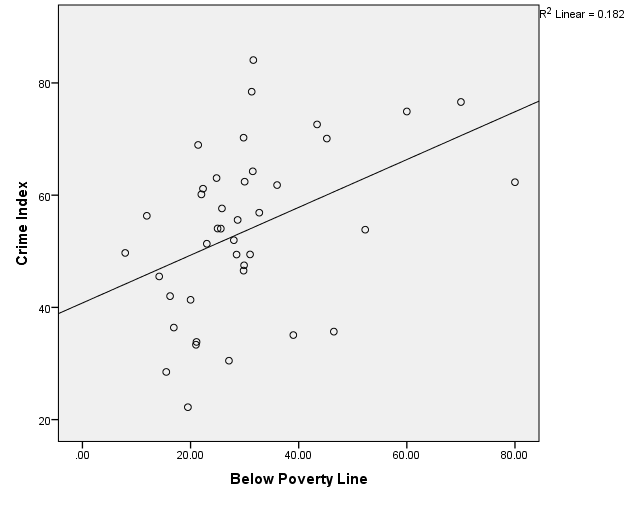
The line of best fit, which is shown in the scatter plot in figure 3 shows a positive relationship between the crime index and the people living below the poverty line.
Table 3.
As shown in Table 3, the Adjusted R Square value is 0.160 which is16%. This is another indicator of the weak relationship between poverty and crime index. The regression test calculated on excel as shown in table 4 shows that the values of interest, which include R2 (0.181) and multiple regression (0.426) are less than unity. This affirms further that poverty is not the only cause of crime, but it is one of the causes of crime.
Table 4.

Scatter plots
The scatter plot, which appears in figure 3, was used to calculate the R2 value, and to determine the line of best fit. It is s critical for determining the nature of the best-line-of-fit. Figure 3 shows the coefficient of determination, R2, which is 0.182 and it measures the total variation of the variable crime index and the below poverty line. This is where the regression of the crime index on the ‘below poverty line’ is shown to be 16%.In theory, when R2 is below 2%, it is deemed to be weak. In this result, the R2, value is 0.182, which shows that despite the relationship between the crime index and the people living below the line of poverty is weak.
Calculating the correlation coefficient
The correlation coefficient is calculated by using the following formula.
It is important to keep the value of r in the range of +1 and -1.a value of r > 0, shows a positive relationship but a value of r <0 indicates a negative relationship among the variables. The correlation coefficient was calculated by running the data on excel Using the excel scatter plot and the CORREL () function, the correlation coefficient was calculated and found to be 0.426023.
Typically, the regression equation is expressed as: y=bx+a
By taking all the values of the Crime Index and the ‘below poverty line’, the regression equation results from the y=0.426 xs+7.449. The coefficients are shown in table 6. These values were used to derive the regression equation as shown.
Table 5.
The Anova test shown in Table 5 provides the F-statistic with a Sig. of.006b, which shows that the level of poverty has a direct effect on the crime index, despite the relationship being weak. The rationale is that the F-statistic is 8.454. Because of the Sig. value is above 0.005, the result must be accepted to be true.
Table 6.
The results in table 6 were used to establish whether as those people living below the line of poverty increase, the crime index increases, and this is confirmed with the positive value of the Beta coefficient of.427. In both cases, the standardized and unstandardized values are positive. Typically, this leads to the equation: y=0.427 xs+7.449. The results show that an increase in the number of people under the poverty line increases the crime in society.
The Chi-square test
Table 7.
It is important to note that the values of the column, ‘Pearson Chi-Square’ are 1520.0 and p-0.241respectively. This shows there is some degree of association between living below the line of poverty and the crime index is weak. Such a weak association shows that there are other factors except for poverty that can be associated with crime.
Accuracy of the results
Various statistical measures such as internal and external validity were used to evaluate the accuracy of the statistical output (Foster, Diamond & Jefferies 9). The results for the test statistics were conducted on a 0.01%, 2-tailed significance test, and the findings were pegged on secondary data. A causal relationship was established between the two variables despite the threats such as a central threat.
The accuracy depends on various factors which include the tools that were used to collect the data and the interpretation that was done on the statistical results. Based on the various tests, it is imperative to note that a high degree of accuracy was achieved because the consistency of the results happens for different statistical tests. The association between the percentage of people living under the poverty line and the crime index is positive for each test.
Implication of the results
The analysis shows two things. The first one is that crime cannot be completely attributed to poverty. Other reasons that lead people to commit crimes in society exist and poverty is one of them. This is revealed in the low R2 value and the Pearson Chi-Square of.241among other statistical measures.
Reliability of the results
To make the results reliable, this investigation used historical data from the past years. Besides, various statistical tests were done on the data to check for consistency and reliability. This was an effective way of solving the statistical problem by using historical data. Single group threats based on history threats is where changes in crime index happen as a result of changes in economic and political variables presented the greatest limitations. The second limitation was due to the selection-testing threat where differences happen in variables that define the groups being tested.
Here, the explanation for this is that a country can be at war or face increased levels of poverty and declining levels of income but declining levels of crime. When such cases have been detected, it is necessary to conduct further studies to determine other causes of crime.
Works Cited
Bradshaw, Jonathan. The Well-being of Children in the UK. Policy Press, 2016.
Foster, Liam, Ian Diamond, and Julie Jefferies. Beginning statistics: an introduction for social scientists. Sage, 2014.
Jones, Gareth Stedman. Outcast London: a study in the relationship between classes in Victorian society. Verso Books, 2014.
Sudbury, Julia. Global Lockdown: Race, gender, and the prison-industrial complex. Routledge, 2014.
Townsend, Peter. International analysis poverty. Routledge, 2014.
Wolf, Achim, Ron Gray, and Seena Fazel. “Violence as a public health problem: an ecological study of 169 countries.” Social Science & Medicine vol. 1, no.104, 2014, pp. 220-227.