Renewable Energy and Transport Fuel Use Patterns Essay

Introduction

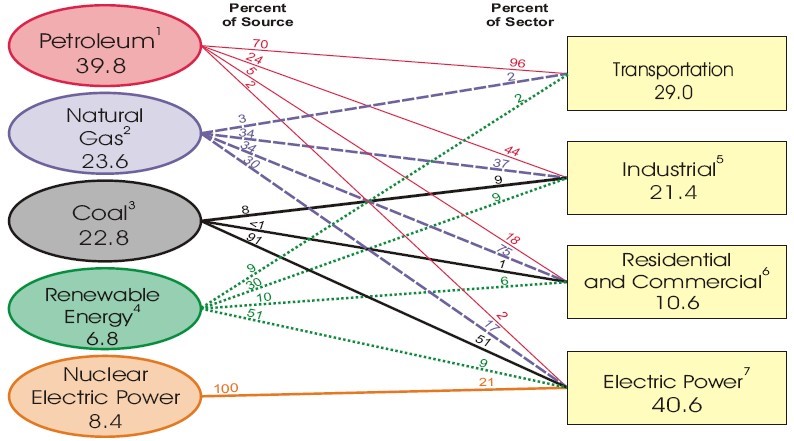
As policy-making and social consensus unite in favor of stopping climate change in its tracks, it seems vital to assess the degree of change in use of primary energy sources that has actually taken place. The latest available annual review (see Figure 1 alongside) reveals that the challenges remain formidable. The largest “consumer” of primary energy is the power generation industry but “clean” nuclear power and renewable energy together contribute less than a third of energy inputs. No less than nine in ten BTU or “therm” equivalents provided by coal also goes to the power sector.

The transportation sector ranks second in total energy use and is very often the focus of media attention because of the American love affair with cars. The publicity about hydrogen, solar and electric hybrids aside, petroleum still accounted for 96% of energy use at least as of the end of 2007.

Data Analysis

The base data is as follows:

Table 1: Energy Information Administration.

The first segment of this analysis tests for differences between consumption of natural gas and ethanol. Owing to the different power trains required by natural gas and ethanol, we assume that the populations of users are distinct. One way to assess whether patterns of natural gas and ethanol use are similar or distinct is to employ a two-sample t test. Since we further posit that the differences can go either way, we employ the two-tailed test. The formal procedure involves formulating hypotheses to be tested as follows:

• H₀, the null hypothesis = There is no difference in the population means for both ethanol (μ₁) and natural gas (μ₂). In technical terms, μ₁ – μ₂ = δ₀.
• H_a, the alternative hypothesis = There is a difference between the population means of ethanol and natural gas. In technical terms, H₁: μ₁ – μ₂ ≠ δ_0.

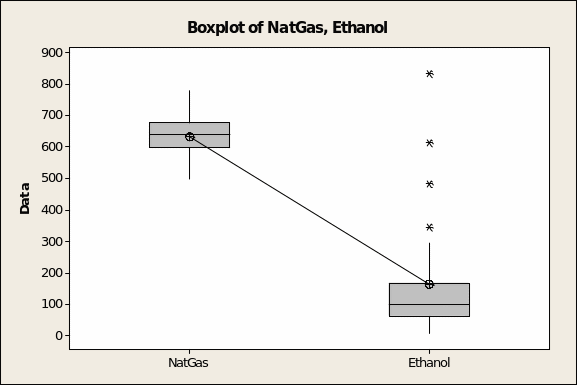
Natural gas has enjoyed a longer tradition of use, starting in this data series (year 1=1973) with around 4.2% of the energy contribution of the motor fuels gasoline, diesel, jet fuel, etc. On the other hand, there was little measurable use for ethanol prior to 1981, when biomass accounted for 6.9 trillion BTU’s of transportation sector use. This factor alone explains why the means for the two fuels are so far apart (averaging 633 trillion and 165 trillion BTU’s, respectively, for NG and biomass, see Table 2 and Figure 2 overleaf). At 467.3, the mean difference between the two fuels lies within the bounds of the 95% confidence interval of the difference (390 at the lower bound and 545 at the upper bound). The magnitude of these results is confirmed by the finding that the significance value for the two-tailed test, s < 0.001, is below the rigorous cut-off of p ≤ 0.01. Since such a difference could have occurred purely by chance less than once in a thousand re-sampling passes, one rejects the null hypothesis, accepts the alternate and concludes that natural gas has historically had better acceptance than the “cleaner” alternative, available for over a quarter of a century now.

Table 2. Two-sample T for NatGas vs Ethanol.

• Difference = mu (NatGas) – mu (Ethanol)
• Estimate for difference: 467.3
• 95% CI for difference: (390.0, 544.7)
• T-Test of difference = 0 (vs not =): T-Value = 12.31 P-Value = 0.000 DF = 32

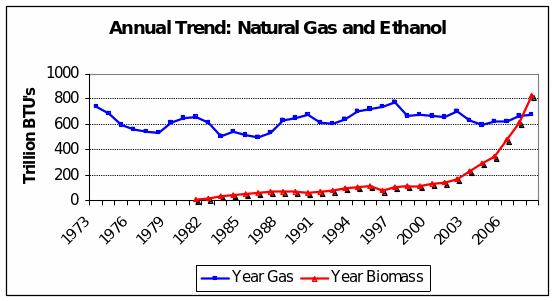
In fact, the annual trend reveals that liquid natural gas fluctuated within a fairly narrow band from about 500 trillion BTU’s to 800, presumably because final cost was linked to OPEC-engineered crude price increases. On the other hand, ethanol use took off starting 2002, surpassed LNG last year and looks to be in the early stages yet of the product life cycle. Car owners are rational enough to adopt the cleaner fuel that is domestically produced and the price of which is not directly linked to anything that happens in the Middle East.

Next, one opted for a one-way ANOVA on the continuous variable distance travelled (“miles car is driven”) against the recode of miles per gallon into the categorical “low/high” MPG class variable. The relevant hypotheses are therefore articulated as:

• H₀, the null hypothesis = Mean distance driven is equal regardless of car model mileage.
• H_a, the alternative hypothesis = Better mileage induces car owners to use their cars more.

The derived F value (see Table 3 overleaf) suggests that the differences in distance driven across cars of different mileage categories (a mean distance of 9,511 miles historically [or at least since 1949] and 11,599 miles in years when the national average broke the 20 MPG barrier) is so great (p < 0.001) as to preclude random chance. In fact, Minitab returns an Adjusted R² suggesting that mileage improvements explain fully 97.9% of the variance in distance Americans take their cars.

Table 3. One-way ANOVA: Mileage, MPG class.

S = 751.1 R-Sq = 97.88% R-Sq(adj) = 97.86%

It would therefore seem that plans by the EPA to raise the nationwide fuel efficiency standard to 35 MPG and that of the nation’s most populous state, California, to require 40 MPG by 2020 (Stoffer, pp. 8-9) will be counterproductive for the goal of reducing total emissions.

Works Cited

1. “Annual Energy Review.” 2008. Energy Information Administration, Dept. of Energy.
2. Stoffer, Harry. “Calif. Regulators Shoot for 40-plus MPG by 2020.” Automotive News. Detroit: 2008. Vol. 82, Iss. 6296; 8-9.