In modern society, geometry in architecture relates shapes with mathematical formulae in the realm of numbers and equations based on the coordinate number system. Typically, that is derived from the ancient view of geometry. However, the agency of geometry is based on drawing where the architect communicates meaning and ideas based on a set of conventions and views using lines that are mathematically connected to produce a coherent design to construct the object to completion (King, 2; Putz, 4). Thus, drawing relies on the agency of geometry in architecture, making both drawing and geometry complimentary.
One must exist in the realm of the other. With that brief argument in mind, the agency of geometry has been in existence in the architectural discipline with time and the complementary nature and significance of drawing and geometry as an agency in architecture bearing weight based on different architects. However, geometry as an agency and its significance have been a point of contention in the architectural world in the past centuries with different architects providing different views of the significance of geometry in their works.
A typical example is a difference existing between the perceptions of the significance of geometry in architecture in the works of Borromini’s, S. Carlo alle Quattro Fontane, Rome (1637-41) compared with that of Adam’s, Syon House, Middlesex (1761). Thus, there is a compelling urge to conduct an in-depth analysis of the views presented by different authors on the perceptions of the significance of the agency of geometry in both cases mentioned above (King, 2).
To search into the significance of geometry based on the perceptions of the architecture of the past centuries and their perceptions about the agency of geometry, it is crucial to briefly discuss the importance of geometry as perceived in the past centuries. The importance of geometry emerged in the 17th century when a church, despite the scarcity of financial resources and a tiny site, was erected at the four fountains intersection in Rome in 1643 based on a design by Francesco Borromini (King, 2). The design was a demonstration of the significance of geometry which showed how the design evolved from an elongated cross to an oval, then an octagon.
Typically, that design was based on an underlying geometrical structure that had different shapes amalgamated into the single geometrical shape, the design that was translated into the final building. Though it has been contended that these shapes had been redrawn in the successive centuries, other researchers contend that position by asserting the significance of geometry in the design and construction of the church in 1634 (Mostafavi, 3).
The geometry of the church had an underlying mathematical relationship in which different shapes were integrated into a single shape. These shapes included two triangles sharing a common base with perpendicular erections projected from their sides, and an inscription of two tangential circles that formed the point of focus that further yielded an oval inscription (Mostafavi, 3).
In addition to that, the geometrical shapes were mathematically related with a double rail rectangle that was tangential to the oval created in the short segment, and chapels that had a semicircular orientation along the major axis with four columns (Mostafavi, 3). The entire geometrical structure was reduced to an octagon by champers introduced into the corners of the rectangles leading to the completion of the design and the final structure of the chapel.
Typically, the importance of geometry provides the basis for argument on the significance of geometry in the cases of Borromini’s, S. Carlo alle Quattro Fontane, Rome (1637-41) and that of with Adam’s, Syon House, Middlesex (1761).thus, to provide a detailed view leading to the distinction between the perceptions of the importance of the agency of geometry in both cases, it is crucial to begin by examining the perceptions developed by Evans (Mostafavi, 3).
In both cases mentioned above, the differences in the agency of geometry are crystallized by discussing both cases about the significance of the agency of geometry from the perspective of Adam’s, Syon House, Middlesex, (1761) and that of Borromini’s, S. Carlo alle Quattro Fontane, Rome (1637-41) (Mostafavi, 3).
One of the writers who have discussed in detail the perspectives of geometry about Adam’s, Syon House, Middlesex, (1761) is Robin Evans. Robin Evans begins by viewing ordinary things as containing mysteries that are resolved as one makes an inquiry from the surface of things into the inner nature of things. While Borromini’s, S. Carlo alle Quattro Fontane, Rome (1637-41) begins their observations by seeing objects architectural structures with mathematical relationships, Adam’s, Syon House, Middlesex, (1761) views any object to consist of doors and windows that are culturally oriented and based on domestic architecture.
Typically, in their argument, information unfolds that shows Adam’s, Syon House, Middlesex, (1761) views to be more philosophical than mathematical in their arguments. One of the solid foundations of their argument is based on the geometry of the eye view. Typically, the argument shows that geometry is deeply founded in drawings that stimulate the imagination. However, these assumptions are confronted by the need to distinguish between architectural drawings and the artist’s use of drawings to stimulate imagination (Mostafavi, 3). However, it is crucial to distinguish the work of art and architectural drawings in the quest to discover the underlying evidence of the significance of geometry in architecture based on both views.
The distinction between architecture and art is based on the conclusion that the artist draws to communicate an idea in the form of a sculpture while on the other hand, an architectural drawing results in translating an idea in the form of a design into a building(Mostafavi, 3). That concludes the fact that the resulting design is based on the underlying geometrical principles. Typically, from the perspectives of Adam’s, Syon House, Middlesex, (1761), geometry provides the basis for translating one form to another without alterations. It is significantly important at this point since it provides the basis for designing anything that can be translated into a building.
Typically, “anything” can exist in the mind from which the idea is translated into a design and later into a building through geometrical means. These designs that are translated into buildings are based on the analogy of creating empty spaces in drawings. Typically, the drawing is presented using colors and other forms to communicate meaning by creating geometrical shapes that convey meaning to the intended audience. However, it is worth noting that Adam’s, Syon House, Middlesex, (1761) views on the significance of geometry draws on philosophical assumptions based on the view of the eye and the imagination of the mind (Mostafavi, 3).
Geometry, from Adam’s, Syon House, Middlesex, (1761) view indicates that geometrical shapes can be created using lines and the architect’s mind. However, at this point, Adam’s, Syon House, Middlesex, (1761) does not provide a clear view of the relationship between the geometry of the shapes created and their mathematical relationships. However, their argument draws heavily from the works of art, and the approach used to maneuver shapes making the projections tangible. Typically, it draws on the geometry of orthographic projections (Mostafavi, 3).
Orthographic projections provide a means for fitting geometrical shapes into others and providing the final object which in this case is a building. The geometry discussed here Adam’s, Syon House, Middlesex, (1761) is based on practical rather than a translation from drawings based on lines into the resulting object. That is demonstrated in the drawings of Palladio’s sketch that demonstrates the relationship between geometrical shapes and the close alignment between a drawing and a building is clear. Typically, the significance of geometry about the chapel mentioned above is based on orthographic projections, where one point of a drawing leads to the creation of another point in a drawing (Mostafavi, 3).
A typical example that discusses the perspectives of Adam’s, Syon House, Middlesex, (1761) based on orthographic projections shows how patterns emerge and are created as a result of other patterns. Typically, the orthographic projections can be in any angle of protection, either first or third angle projections. In either of the projections, one form of a drawing leads to the creation of diverse views of other views. In addition to that, the significance of geometry, in this case, is based on translating reality from the virtual world (Mostafavi, 3).
The following is a descriptive example of orthographic projections based on underlying principles of geometry used in the construction of a dome. According to the underlying geometrical principles is a dome with a floor consisting of curved ribs form the focus at an oculus ring.
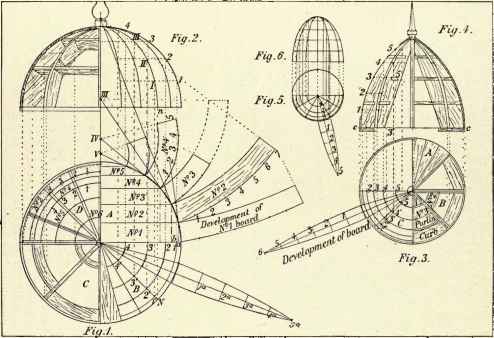
It is possible to realize that the drawings are orthographic projections of a dome with the projection lines based on the geometrical principles that underlie the construction. Typically, the curvatures are not allocated names but are produced based on their points of intersections with other points in the dome. That results in several drawings being made from an original object that had its origin in the work of the imagination of the mind. Typically, the geometrical principles that, lead to the final project or product are based on orthographic projections. One can argue on the significance of orthographic projections, the imagination of the mind, the significance of a drawing, and their link to the geometry that translates a drawing into the final building (Mostafavi, 3).
Typically, one can see that parallel projections are produced on a plane that is circular onto a hemisphere that is further transformed into another figure with a requisite number of projections. Thus, formal circles lead to the generation of several lines and intersections leading to different views of the same design. The actual plan based on the above is the annular shape. Though the resulting figures look like circles or semi-circles, the geometry of origin is much more expendable and does not look like the final product which is a beautiful dome. However, it is crucial to work based on acquired technical drawing skills to produce such a design with the requisite accuracy for transformation into an actual design and gradually a building (Mostafavi, 3).
In theory, orthographic projections, according to Adam’s, Syon House, Middlesex, (1761) views are among the techniques used in the architectural world to provide and develop designs that translate into buildings (Evans, 25). Typically, the argument has its basis on projections, a radical departure from essentialism, a cultural perspective of architecture. In essence, one can see the underlying principles of orthographic projections to be based on the translations and transitions. Typically, translations provide the basis for transforming a drawing produced based on orthographic geometrical principles into a complete design and gradually a building.
It is worth, therefore, noting an additional view in Adam’s, Syon House, Middlesex, (1761) of the significance of geometry based on orthographic projections based on translations from one form into another (Michael, 1). However, in a nutshell, the translations and the projections are based on geometric patterns produced with such precision that little or no loss of the original object occurs in the transformation of the transition stage (Evans, 30). Having evaluated Adam’s, Syon House, Middlesex, (1761) views on the significance of geometry in architecture, it is worth examining the significance of geometry about the perceptions in Borromini’s, S. Carlo alle Quattro Fontane, Rome (1637-41) (Michael, 2).
In Borromini’s, S. Carlo alle Quattro Fontane, Rome (1637-41) views, the significance of geometry is based on another perspective and seems to show some radical departure from that provided by Adam’s, Syon House, Middlesex, (1761) views. In Borromini’s, S. Carlo alle Quattro Fontane, Rome (1637-41), geometry is the underlying rationale for a shape that is produced by an ordered sequence of items arranged in an orderly manner to produce the final design and building. Typically, the sequence consists of translations that occur in a specified ratio (Michael, 4). The underlying transformation is executed using lines as the connecting points for the transformations to occur.
One could readily see these lines as orthographic projections, thus, annulling the previous basis of arguments that geometry is based on orthographic projections, which is not the case. In the Borromini’s, S. Carlo alle Quattro Fontane, Rome (1637-41) case, there is the mathematical relationship that the former seems not the be aware of since their views originate from the mind and tend to take an artistic form which, however, radically departs when considering the underlying objectives of producing an actual building rather than a work of art such as a sculpture. In the apparent departure from Adam’s, Syon House, Middlesex, (1761) and yet a demonstration of the significance of geometry as provided by Borromini’s, S. Carlo alle Quattro Fontane, Rome (1637-41) views, a plan or design begins from a specific point as the origin of the entire plan.
However, both views regard drawings as the basis of any design (Michael, 6). A typical example in the drawing is just to identify a point and set the drawing instrument, in this case, the compass, open it to the right width and taking a specific point as the center, draw the first arch. Then, the next step follows by making arcs that make several intersections and center points to allow one to draw other arcs by taking the points of intersections as the centers of other subsequent arcs (Evans, 45). These arcs intersect at various points which are then joined to produce the desired design. It is important to note the significance of the geometrical intricacies introduced into the design by making several arcs that result in a specific design. Of course, the design can be translated into the final product which in this case is the building (Michael, 7).
In the design, due consideration is taken when producing the central points of intersection that lead to the creation of the Inner and Outer lines of San Carlo (Evans, 25). Typically, a summary of the construction process of the design is based on the use of a scale along the horizontal axis, and the setting of the compass used in the drawing to draw the bingo and the vertical axis along which the inner and outer lines of San Carlo are drawn (Michael, 10). As mentioned elsewhere, the geometry relies on the use of mathematical ratios, and these measurements are related to the curvature of the lateral chapel. It is important to see that each of the intersections produced and the resulting shapes have strong relationships with geometry used and the imagination of the mind.
It is worth noting that in the process of developing the plan for the San Carlo, site characteristics were also constructed as previously mentioned that it was constructed on a restricted site with limited financial provisions (Evans, 25). Thus, the gradual development and result of the plan showed that the resulting plan fitted exactly based on the geometrical intricacies that factored the construction site and the precision with which the design fitted into the selected site. However, without making a detailed analysis and description of the design and construction of the San Carlo chapel, it is important to evaluate the significance of geometry in the above case (Michael, 15).
It is critical to note that the author had formal knowledge of the techniques articulated by scientists of the time such as Kepler in formulating the geometrical relationships consisting of different shapes. In this case, Borromini makes use of the complex relationship existing between geometrical shapes and their mathematical relationships. In addition to that, it is worth noting that Borromini had developed a close relationship between the oval shape and geometrical relationships, by integrating both in the design to produce a design that fitted precisely into the requisite construction site.
Typically, Borromini’s regard for the complex relationships that can be developed using different geometrical principles is exemplified in the rigor with which the drawings of the San Carlo are produced with the underlying geometrical principles used to attain high precision. In addition to that, the San Carlo drawings are based on the use of lines with mathematical significance imbued in the geometrical principles used in the design of the building. However, it is crucial to note that both authors provide a sound basis for modern architecture and one is led to the conclusion that modern architecture can richly benefit from the experiences and perspectives of the significance of geometry in architecture when both are integrated.
Works Cited
Evans, Robin “The Developed Surface: An Enquiry into the Brief Life of an Eighteenth-Century Drawing Technique”, Translations from Drawing to Building and other Essays, London: Architectural Association, 1997. Print.
King, David. The Complete Works of Robert and James Adam, Oxford: Butterworth, 1991.
Michael, Hill, “The Curvature of the Lateral Chapels in San Carlo alle Quattro Fontane”, Julia Gatley (ed) Cultural Crossroads, SAHANZ: Auckland, 2009.
Mostafavi, Mohsen. Paradoxes of the Ordinary. Web.
Putz, Claus 2010, Teaching Descriptive geometry for architects: Didactic Principles and Effective methods Demonstrated by the Example of Monge Projection. RWTH Aachen, Germany. Institute for Geometry and Applied Mathematics. Web.