Introduction
In this project, we are interested in determining if there is any relationship between the dependent variable (GPA) and the independent variables (final marks and the total). In this study, we will use the Pearson correlation coefficient and the Spearman rank correlation coefficient to determine if there is any relationship between the dependent variable and independent variable. We assume that the variables are normally distributed and are continuous. The association between the dependent variable and independent variables will be examined using the Pearson correlation and the spearman rank correlation.
Data description
In this project we are using a sample size of 105 and the data has 4 variables gender, GPA, final, and totally. The dependent variable is the GPA, the independent variables are; Final marks, and the total marks. The measurement of these variables is the ordinal and the sample size is 105. The variables GPA and final marks have continues variables.
Testing the assumption of normality
The assumptions of the correlation analysis are that the data are normally distributed. To access these assumptions, we conduct a normal probability plot and determine the kurtosis and skewness of the data.
Hypothesis
The null hypothesis; there is a relationship between the GPA and the final exam marks. The alternative hypothesis; there is no relationship between the GPA and the final exam marks.
The alpha is 0.01
Table 5: simple regression model
The value of R- square is 0.008. This implies that the regression model can be able to account for 0.08% of the errors in the regression model the adjusted R square is equal to -0.12 and the standard error of the estimate is equate to 0.28974.
The multiple regression model
Table 6: The multiple regression model
From the analysis of variance we can observe that the value of the F-statistic is equal to 0.403 which have an F- statistic equal to 0.669 which is greater than the 0.05 level of confidence. Since the significant value is greater than the 0.05 level of confidence, we conclude that there is significant relationship between the GPA and the final marks of the students.
Simple regression
Table 8: the coefficient of regression
From the above analysis of variance, the relationship between the gap, the final and the total marks is significant at 005 level of confidence. This is because the significance value is equal to 0.669 which is greater than the 0.05 level of confidence. For individual independent variables, the final and the total marks are significant to the gpa.
Results and analysis
In this section we will analyze the correlation coefficient of the pair of variables. In this we are determining if there is any relationship between the variables. The variables in this section are; the GPA, the total grade, and the final scores. A Pearson correlation coefficient will be used to determine if there is any relationship between the pairs of variables. A Spearman correlation coefficient will also be determined for every pair of variable.
Ppartial correlation vs non- partial correlation
Results of section 1 analysis
Table 9: partial correlation vs non- partial correlation
From the above analysis, there is a relationship between GPA and the final grade. This is because the Pearson correlation coefficient is 0.865 and the significant value of 0.000. This implies that there is a relationship between the GPA and the final grade of the students. The value of the Pearson correlation between the GPA and the total marks is equal to 0.-0.07 which has a significant value of 0.475. There is no relationship between the GPA and the total student marks are not related since the significant value is greater than the 0.01 levels of significance.
Table 10: The spearman rank correlation
The value of the spearman rank correlation between the variable GPA and the final marks is -0.042 which have a two tailed significant value of 0.674 which is greater than the 0.05level of confidence. Since the two tailed significant value is greater than the 0.05 level of confidence, we can conclude that there is no significant evidence to conclude that the variable GPA and the final marks are significant. The value of the spearman correlation between the GPA and the total marks is -0.053 which have a two tailed significant value of 0.589 which is greater than the 0.05 level of confidence. Since the two tailed significant value is greater than the 0.05 level of confidence, we conclude that there is no sufficient evidence to conclude that the variable GPA and the total marks are significant at 95% confidence. The value of the spearman rank correlation is 0.875 which have a two tailed significant value of 0.000 which is less than the 0.05 level of confidence. Since the two tailed value is less than the 0.05 level of confidence, we conclude that there is sufficient evidence to conclude that there significant relationship between the total marks and the GPA.
Table 11: The descriptive statistics
From above descriptive statistics, the skewness statistics value is 0.146 and a standard error of 0.236. The kurtosis statistics value is -1.310 and the standard error is 0.467.
The scatter plot
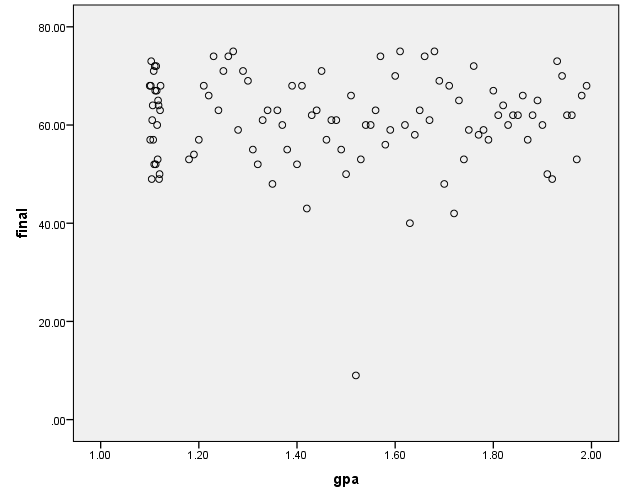
From above scatter plot, there is only one outlier and thus the data is fairly good for analysis. From the output of section 2, there the data is normally distributed and the data is continues hence we can say that data on GPA and final has a satisfied the assumption of correlation.
Conclusions
From the above analysis, there is a relationship between GPA and the final grade. This is because the Pearson correlation coefficient is 0.875 and the significant value of 0.000. This implies that there is a relationship between the GPA and the final grade of the students. There is no relationship between the GPA and the total student marks are not related since the significant value is greater than the 0.01 levels of significance. From above scatter plot, there is only one outlier and thus the data is fairly good for analysis. From the output of section 2, there the data is normally distributed and the data is continues, hence we can say that data on GPA and final has a satisfied the assumption of correlation. Correlation analysis just indicates if the variables are related or not. In this case, it does the relationship between the variables and thus it’s advisable to use the regression analysis to obtain the nature of relationship between the variables.
Logistic regression
Variable description
The variables to be used in this logistic regression are the experience as the dependent variable, the occupation, and the companies worked for. The variables are all nominal and are continuous.
The dependent variable is the experience of the job while the independent variables are the occupation, and the companies worked for.
From the above logistic regression, we can observe that the logistic regression model can be used to predict the work experience given the occupation and the companies worked for.
From the coefficient of the logistic model, we can observe that the variables occupation and companies worked for are significant since the two tailed significant level are equal to 0.000 which is less than the 0.05 significant levels.
References
Kelle, G. (2014). Statistics for Management and Economics, (10thed.). New York: McGraw-Hill/Irwin.
Kutner, M., Nachtsheim, C., Neter, J., & Li, W. (2005). Applied Linear Statistical Models (5th ed.). New York: McGraw-Hill/Irwin.