Introduction
The essence of performing this experiment was to verify the relationship between the effects of force on the extension of a coiled spring and as such, verify the principle behind a spring balance.
The experiment was approached courtesy of a vertically mounted panel upon which two springs, one under compression and the other under extension, were suspended and subjected to their respective forces and their corresponding changes in length recorded for analysis. The essence was to subject these two springs under the force of gravity and as such draw a correlation between the change in length and the applied force. Consequently, this relationship would aid in understanding the principle behind the calibration of a spring balance.
From the experiment, it was clear that both the compressed and the extended springs changed their lengths proportionately with the change in the applied forces. Hence, the springs obeyed Hooke’s law for elastic materials. This principle is the basis for spring balance calibration.
Experimental Objective
The objective of this experiment was to verify the relationship between the effects of force on the extension of a coiled spring and as such, verify the principle behind a spring balance.
Theoretical Background
When a coiled spring is subjected to either extension or compression forces, it will extend or compress respectively. With the status quo, the spring possesses some energy vital in the construction of equipment that displays cushioning effects under stress. Among the equipment are shock-absorbers, buffers and engine values. Besides displaying cushioning effects, a coiled spring is understood to be the single most important element of a spring balance (Slaughter 9). Under varied extension forces, the extension of a coiled spring is understood to be proportional to the same. As such, designers of spring balances selectively design spring balances for measuring weights within a certain bracket. This is so because beyond some critical value of the weight the spring balance ceases to be effective. For this reason, a spring balance intended for measuring heavy loads makes use of stiffer springs that are less sensitive to lighter loads. On the contrary, spring balances intended for measuring lighter loads makes use of more sensitive springs.
In order for a coiled spring to be used to measure weights of different bodies, they need to be calibrated to give accurate measurements. The relationship between the stretching force and the extension is understood to be proportionate within the stretching limit. This is explained by Hooke’s law which states that for an elastic material, the stretching force is directly proportional to the stretching force as long as the elastic limit is not exceeded. Correspondingly, when the spring is subjected to compression force it obeys Hooke’s law (Slaughter 10). The correlation between the stretching force and the extension means that a spring balance traces a uniform scale. This principle forms the basis for calibration for spring balances.
Experimental Procedures
In the first experimental setup, a mounting panel was mounted vertically upon which a stretching spring was suspended ready for analysis. A weight hook was later hung at the lower end of the spring ready for suspending weights. A piece of paper was then mounted on the mounting panel such that the position of the hook is biased at the top of the page. The lower level of the hook was marked against the paper using a pencil and a set square. A 1N weight was later hung on the hook after which the lower end of the hook was marked against the paper. The weight and its corresponding extension were recorded for analysis. A 1N weight was added one at a time as their corresponding extensions were being recorded. These were added to a maximum of 5N and later used for analysis. Upon reaching the 5N mark, the reverse was done to confirm that the marks coincide.
In the second setup, the initial spring was replaced by a shorter one while maintaining the step-by-step procedure of the same. In the third setup, however; the arrangement was the reverse in that it was based on compression rather than an extension. 1N weight was added one at a time just like the previous experiment after which off-loading was done step by step.
Experimental Data
The data obtained from the experiment is as shown below:
Table 1 for the first test (long spring);
Table 2 for the second test (shorter spring);
Table 3 for compressed spring;
Data Analysis
According to Hooke’s law;
Force (F) is directly proportional to the extension (e).
Therefore,
F ∞e hence,
F=ke
k is the spring constant which depends on the stiffness of the spring.
On plotting F against e, a straight line is obtained:
The first test:
Graph 1 of Force against an extension for the long spring:
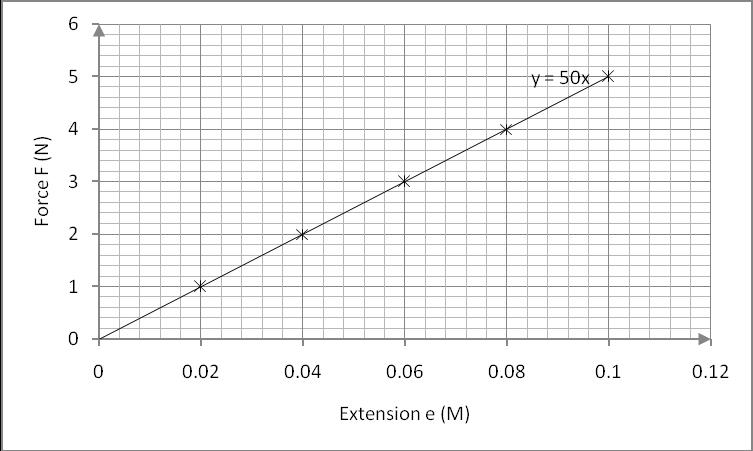
F= ke
K (spring constant)= gradient= (change in force)/(change in extension)= 50 N/M
Therefore; F=50e
The second test;
Graph 2 of Force against an extension for the shorter spring:
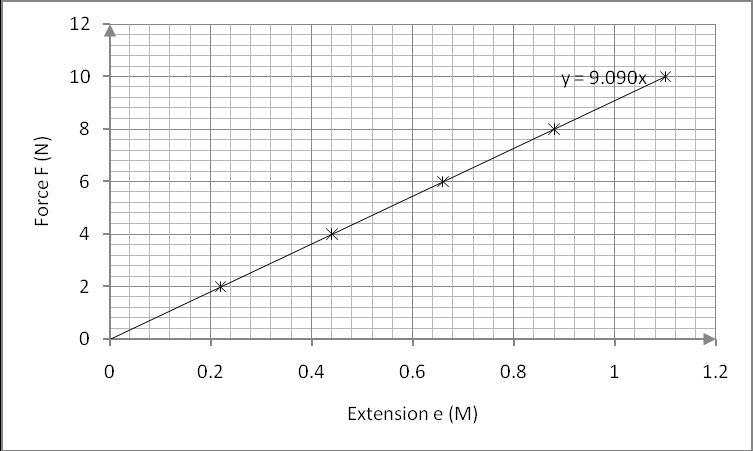
k=9.09N/M
Therefore; F=9.09e.
Test 3 for compressing spring.
Graph 3 of force against extension:
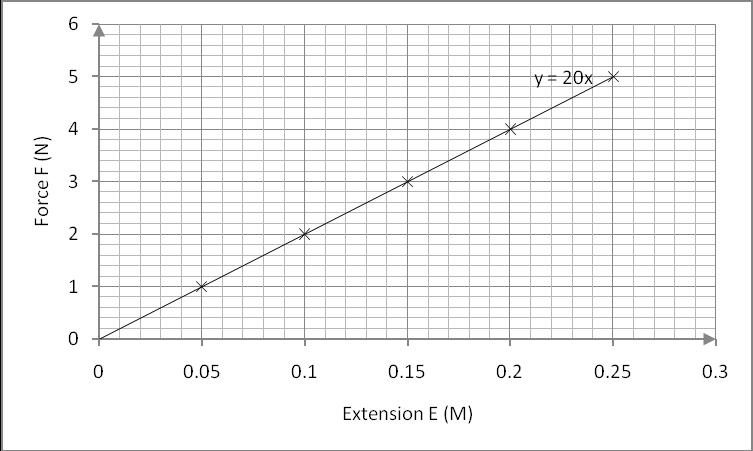
k=20N/M
Therefore; F=20e.
Discussion
The objective of this experiment was to verify the relationship between applied force and extension for a coiled spring subjected under either compression or extension forces. According to Hooke’s law, the relationship between the two ought to trace a linear relationship. As such, the force should be directly proportional to the extension as long as the elastic limit is not exceeded. The constant of proportionality, k, determines the strength of a spring balance. On comparing the strengths of springs, the strength increases with the increase in the value of k. For this reason, a strong spring is meant for weighing heavier loads while the opposite is meant for lighter loads.
On comparing the plots of the graphs for the springs it is clear that they obey Hooke’s law. Thus, from the three graphs, it is clear that the applied force is directly proportional to the extension. This principle comes in handy when calibrating springs. From the calculated values of kit is evident that the longer spring is the strongest (K=50N/M) while the shorter one (k=9.09N/M) is the weakest of the three. The corresponding values of loading and offloading might not be the same because of some slight deformation experienced during loading. For this reason, when using a spring balance to measure weights of loads, it is vital that the values of k be monitored to ensure it is constant to obtain consistent results.
At some point, one would be required to substitute a spring with a new and similar one to maintain consistency. The difference between springs designed for weighing a 1N load and a 1KN load comes in the degree of stiffness numerically illustrated by the bigness in the values of k. Hence, the latter will have a higher value of k than the former.
Conclusions
The main objective of this experiment was to draw a relationship between applied force and the extension of a coiled spring. The relationship was proportionate meaning that the spring extends uniformly with the increase in force. This principle forms the basis behind the calibration of spring balances.
Works Cited
Slaughter, William. The Linearized Theory of Elasticity. Cambridge: Cambridge University Press, 2002. Print.