The Moment of Inertia of a Connecting Rod Report

Aim

The aim of this experiment is to find the moment of inertia of a connecting rod from its vibrations. This is investigated using the compound pendulum method. The equation for the moment of inertia of the connecting rod about its centre of mass as a function of the period of oscillations measured is also determined from the data that is collected from the experiment. The equation is determined for small oscillations.

Materials Used

• Connecting rod
• Calculator
• Ruler
• Timer

Methodology

The mass of the connecting rod was weighed using a weighing balance and the value that was obtained was recorded. The centre of gravity of the connecting rod was then determined and this point was labeled CG. The distance between the small end and the big end of the connecting rod was measured and labeled l. The distance between the centre of gravity and the small end, h₁, and that between the big end and the centre of gravity, h₂, were then measured and their values recorded. The small end of the connecting rod was then used to suspend the rod on a knife edge. It was then given a displacement of 10^o in the vertical plane and released to oscillate freely. A stop watch was then used to measure the time the connecting rod took to complete ten oscillations. The displacement was done three times and each time the time taken by the connecting rod to complete ten oscillations was recorded. The average time was then calculated from these three values to ensure that the errors in the measurements are averaged. Once the average value for a 10^o displacement was calculated, the connecting rod was displaced to an angle of 20^o. Three values of time taken to complete ten oscillations were recorded and the average value found. The rod was then suspended on the big edge on the knife edge. It was then displaced by an angle of 10^o and the average time for ten oscillations determined. The displacement was then made to be 20^o and the average time to complete ten oscillations was determined. These values were then tabulated.

Results and Discussion

The mass of the connecting rod = 958 g.

The length of the connecting rod

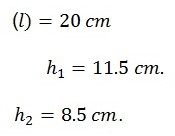
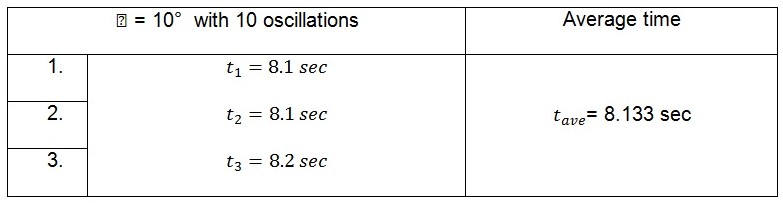
Small end of connecting rod supported on the knife edge

Displacement of 10^o

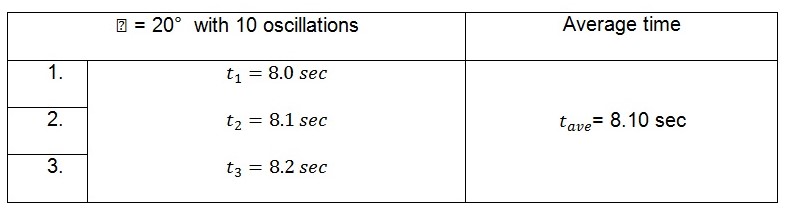
Displacement of 20^o

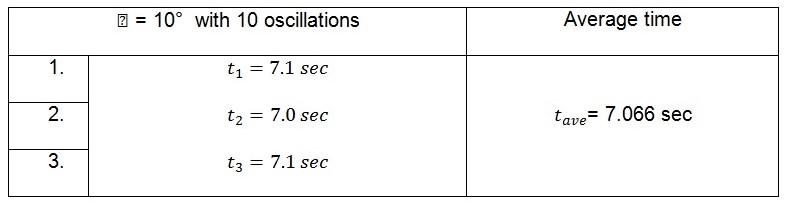
Big end of the connecting rod supported on the knife edge

Displacement of 10^o

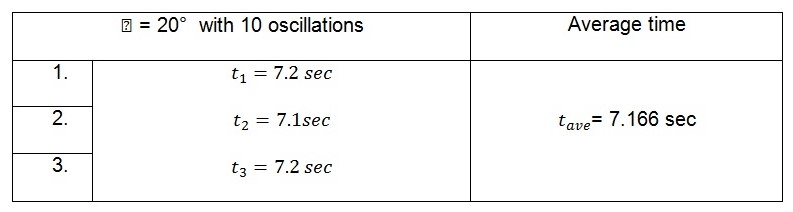
Displacement of 20^o

The restoring angular momentum for the pendulum at an angle θ^o from its rest position is given by the equation below (Hewitt, 2009, p. 125):

Restoring angular momentum = – Force X Distance from the axis of rotation

When the connecting rod is supported on the small end by the knife edge, the expression becomes;

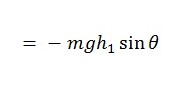
When the connecting rod is supported on the big end by the knife edge, the expression becomes;

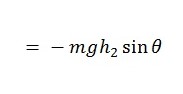
For a case of rotary motion, Newton’s Law’s of motion state that (Hewitt, 2009, p. 109):

Torque = Momentum of inertia X angular acceleration

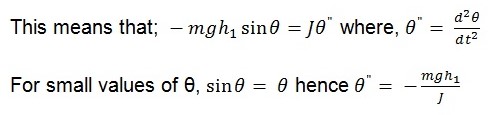
Therefore for an angular velocity of ω the period of the compound pendulum, T that has a constant k is given by (Ciufolini & Wheeler, 1995, p. 256);

The tabulated average values in the tables above represent the time taken by the pendulum to complete ten oscillations. The period of the pendulum which is the time taken to complete one oscillation can be calculated from these values. This is illustrated below.

When the small end of the connecting rod is supported on the knife edge, the values of the period are:

For 10^o,

For 20^o,

When the big end of the connecting rod is supported on the knife edge, the values of the period are:

For 10^o,

For 20^o,

The values obtained show that the period that is obtained when the small end of the connecting rod is supported on the knife edge are higher than those obtained when the big end of the connecting rod is supported by the knife edge. This is because the distances between these two points and the center of mass of the rod vary. The period is more when the small end acts as a fulcrum.

Conclusion

The experiment was successful since all the aims of the experiment were met. The moment of inertia of a body is affected by the shape of the body. This is because the position of the center of gravity of the body affects the moment of inertia and this is affected by the shape of the body. The period of oscillation of a body is affected by the position of the centre of gravity. When the distance between the centre of gravity and the point of support of the body is large, the period also has a large value. On the other hand, when the distance between the centre of gravity and the point of support of the body is small, the period also becomes small. Therefore, the moment of inertia for two objects that have the same mass may be different due to the difference in the distribution in the mass within the bodies.

References

Ciufolini, I., & Wheeler, J. 1995, Gravitation and Inertia, Princeton University Press, London.

Hewitt, P. 2009, Conceptual Physics, Addison-Wesley, New York.