Introduction
The study of the optical laws of reflection and refraction of light is of decisive importance for the optical beam path’s practical research. As is known, light has dualism, from which it follows that it can be considered either as a flow of particles, called photons or as an electromagnetic wave. The basic version of studying these laws does not consider the wave properties of light but instead operates with such quantities as the angle of incidence, refractive index, and distortion. It should be recognized that these quantities are not constant and depend directly on the position of the light source in space and the nature of the medium through which the beam passes. This lab report summarizes what is known about the optical laws of refraction and reflection by considering seven different cases of the light path. The work is a valuable material for students to systematize and structure their knowledge of the physics of light.
Procedure
The laboratory experiment was performed in seven steps. Seven screenshots depicting the diagram of the optical setup for the study are presented sequentially below.
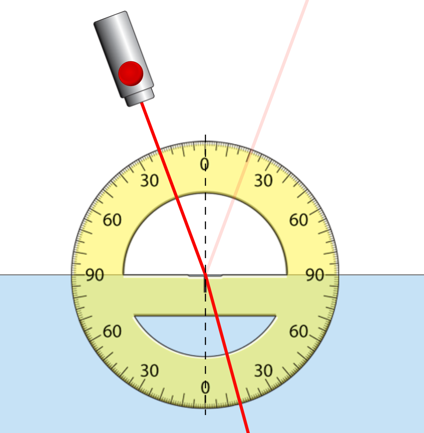
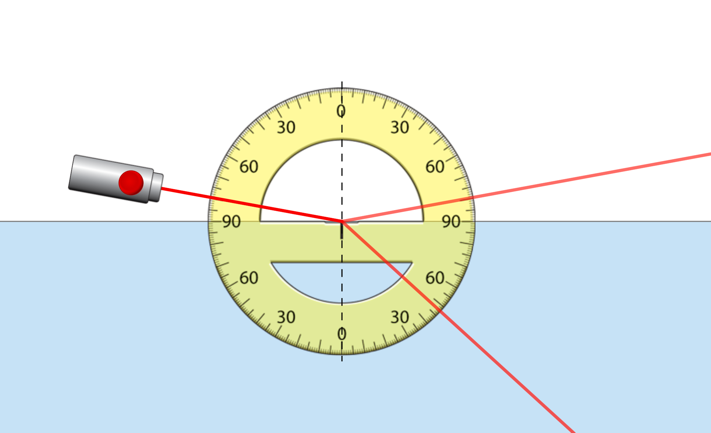
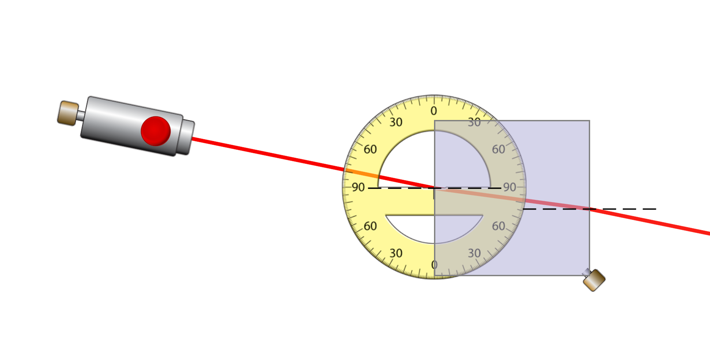
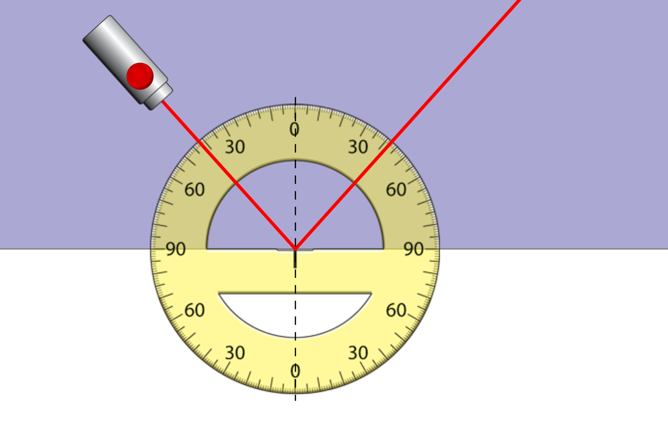
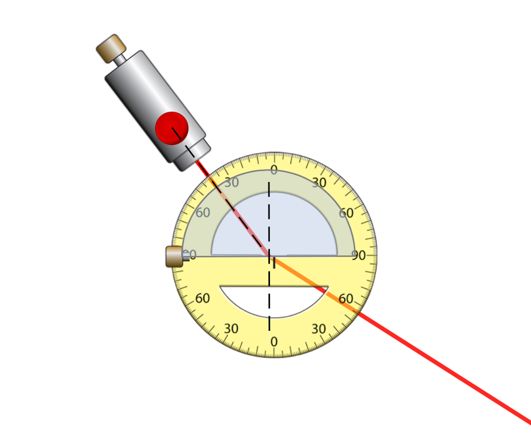
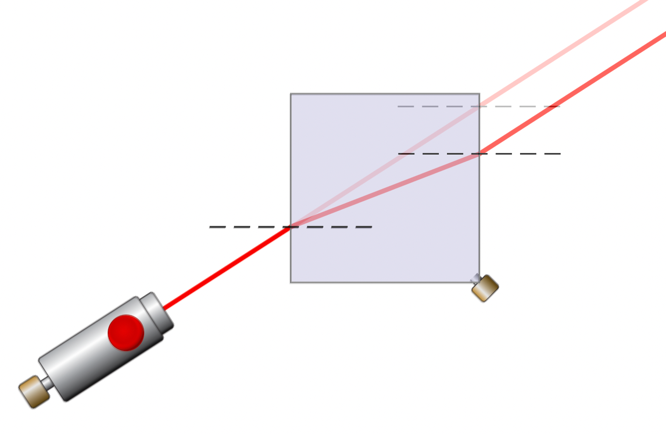
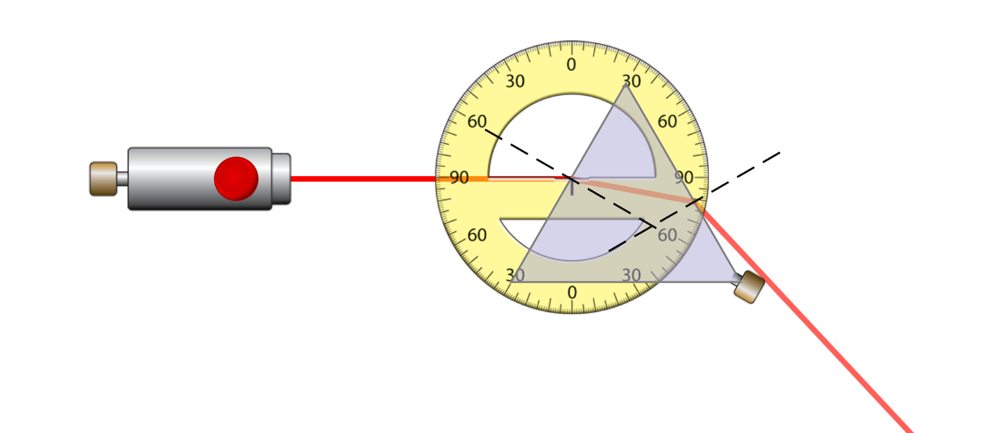
Data Observations & Calculations
The following formulas were used to calculate the corresponding values: percentage error, mean value, refractive index, critical angle, and deflection angle:
Table A. Law of reflection.
Table B. Law of refraction.
Table C. Law of refraction again.
Table D. Total internal reflection.
Table E. Total internal reflection again (since n2>n1, there are no solutions).
Table F. Refraction light ray shift.
Table G. Deviation of light from a prism.
Data Analysis
The data of the tables generally confirm well the known information about the laws of refraction and reflection. Table A showed that the beam’s angle of incidence is numerically identical to the angle of reflection, which was confirmed by a zero percent error. Table B showed that the refractive index could be calculated through the known values of the incidence angle and the angle of refraction. An appropriate formula was used for this purpose. In general, the results were reliable, given the low error. Table C also confirmed that the refractive index could be calculated from the known angles, even if a solid is used as the medium. In this case, the percentage error was already much higher, which was caused by the inaccuracy of the angle measurement in the absence of deeper detail of the virtual instrument.
In addition, since reference data for unknown material B were not available, the error percentage for this case was not calculated. Table D and Table E showed that it is possible to determine the critical angle of refraction of a light beam for two media, with only the refractive magnitudes of the media needed to be known. The error results for these Tables are low, and the error can be fully justified by the inaccuracy of the original ray angle of incidence measurement. The largest errors were noticeable for the case F, in which the measure of the difference between the straight beam and the refracted beam was determined. Since the percentage error averaged 86%, this indicates an extremely low level of test reliability. Case H was not considered because support for the Flash player, which is necessary for the effective operation of the simulator, has been suspended on all modern computers. Table G showed that it was possible to calculate the value of the deflection angle for a triangular prism using the known formula. The percentage errors did not exceed 7.70% for each of the three cases, and any errors were due to a lack of measurement accuracy.
Conclusion
To summarize, it should be said that the work performed entirely confirms the possibility of using the optical laws of refraction and reflection of a light beam. In the work, six out of eight cases were studied due to the impossibility of performing two. The total errors in each of the cases were not too high, and therefore we can declare good reliability of the results obtained.
Reference
Bending light. (n.d.). PHET Colorado. Web.