Introduction
The vacuum chamber is a necessary tool especially in industrial environments where factories rely heavily on them for various industrial practices. It is used majorly for the compression of gases to serve I things like welding. Alternatively it can be used for liquids to compress liquids out for purposes like spraying. It is therefore of absolute importance to consider their construction, since they are sometimes dangerous careers, especially when converted into gas careers as they are, oftentimes. Many are the instances when poor or unscrupulous construction has resulted in explosions and untold damage. The gas explosions have oftentimes caused deaths of technocrats handling the equipment and burning of property of painful costs. To curb such, therefore, attention should be given to its construction with the relevant architectural and engineering principles highly upheld.
Background
Before embarking on the process of the necessities in the construction of the vacuum chamber it would be necessary to think of the kind of materials to be used in the endeavour. This paper sets out to examine how in particular the Top or cover of a vacuum chamber ought to be designed. However, this task cannot be undertaken in isolation of the other dimensions of the camber. Thus, the base of the chamber as well as the cover and the technical factors and principles influencing their construction has been considered in detail.
The history of the chamber actually began with the discovery of the vacuum tube, which can be regarded as its predecessor. The vacuum tube or ‘electron tube’ in its simplest form, the diode, can be likened to a light bulb, which has a heat- and light-emitting filament encased in delicate material. It operates on the logic of its serving as one-way switch and signal amplifier in certain devices such as radios. With all its great novel advantages, transistor technology is perhaps most revolutionary for spurring the miniaturization trend in the electronic industry (Jovanovic and Rousseau, 2002).
Reaction of metals with air and vapour (or water)
This must be considered since if not, certain insidious chemical reactions do occur causing harm to the chamber and exposing its users to danger. While iron would be the most preferred material, there are dangers to it that must be taken care of. Since in any vacuum chamber gases and moisture are bound to be found, rusting of the iron is obvious. Yet this is detrimental to the chamber since it will destroy it with time. This is because tap water or distilled water contains oxygen. If iron combines with oxygen in the presence of water it will form hydrated iron (III) oxide, which is brown. This brown and porous substance is what is referred to as rust.
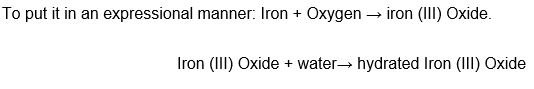
Rusting would even be more if some experiments are to be carried out containing sodium chloride. Be that as it may, it is necessary to take the relevant precaution in preventing this undue occurrence of rusting. Rusting destroys the machinery, any equipment to be used in the chamber and even of the chamber top if made of iron. Prevention of it is therefore paramount. The basis of prevention of rusting of iron or steel is to keep out of direct contact with water and oxygen. The following methods are quite often used: Painting of the chamber and of its top. It is also possible to do coating with other metals. This can be done through galvanization or electroplating. Another useful approach is to utilize alloying. This involves the mixing of one or more metals to produce a substance which does not rust. Finally, oiling and greasing can serve the purpose well. This method is particularly used in moving engine parts where other methods cannot be used due to friction.
While our discussion has quite much dwelt with iron, it does not imply that the options of metals are however reliable for the purpose of vacuum chambers. The other metals as well react with, if not cold water then steam, both of which are to be found in such a chamber. For instance, Magnesium burns brightly in steam to form white magnesium oxide powder and hydrogen gas. Zinc and iron do not burn in steam but they glow. Zinc metal reacts with steam to form yellow powder of zinc Oxide which turns white on cooling. Iron forms a black residue of an Oxide called tri-iron tetra-oxide and hydrogen.
Aluminium reacts with steam but quickly forms a layer of aluminium oxide which prevents further reaction. Lead and copper will however have no reaction and would perhaps be suitable for the purpose.
The Dimensions
The particular design of the chamber we want to develop is one that is cylindrical. Its Top however is not just meant for fitting the chamber, but also for carrying some extra load. For that matter, we have settled on the bottom assuming a square shape that it may be able to gracefully accommodate another material that is cylindrical in shape, the vacuum chamber. A similar square shape would be assumed by the cover to sustain another possibly cylindrically designed material, the welding equipment. Therefore, one cylindrical material would be at the bottom, the chamber in between will be the Top to compartmentalize the two gadgets, and at the top most will be the other cylindrical gadget, the beam welding equipment. However, to make the base stronger than the entire weight, we decided to end up with a square base at the bottom of the chamber.
Cause of up thrust
Since the chamber is to be cylindrical, we must consider a cylindrical solid cross-sectional area A, totally subjected to pressure of density p, as shown in the figure below.
Since pressure increases with depth, pressure of the welding equipment at the top T of the cover (Top) is less than that at the bottom B.
Pressure of the weight at a given depth acts equally in all directions. Hence, pressures on the sides of the solid cancel out. If p is the atmospheric pressure, pressure PT at the top of the cover (Top) is given by;
PT = P+ h1pg
We can thus determine the weight of the square bottom.
Since force= pressure × area, Force FT acting o top of the object is given by;
F1=PTA
= (P+h1pg) A
Force FB acting on the bottom of the solid;
FB= PB A
= (p+h2pg) A
The resultant upward force is hpgA, where h=h2-h1. This resultant force is the upthrust, U.
Thus, U=hAgp
=Wpg
Where weight W of the chamber and the object on top is given by, W=Ah.
Completing the square base
The chamber itself after construction cannot be expected to suspend in the air or be put on the bare ground. This will facilitate its vulnerability to dangers like being hit by other objects. Moreover its cylindrical shape may also make it difficult to let stand at an angle vertically perpendicular to the ground. As such, it is necessary to create a base for it. However, since the chamber is already complete, we only need to get a formula that will favour a square base and constitute the figures reflected by the chamber’s dimensions in the aquatic equation. Moreover, since the desired base design is square, a quadratic rather than an aquatic equation will serve the purpose better
Any quadratic expression can be simplified and presented in the form ax2+bx+c, where a, b and c are constants and a ≠ o. you will notice that in all these cases, (b/2)2 =c. for this expression to be used to find any side of the square base, we must deal with a case where a=1, for instance:
In x2 +10 x2, we must find out what can be added to make it a perfect square. We shall use this relationship to make the expression a perfect square so that we determine the dimensions of the lower support part of the chamber.
Solution
Let the number to be added be a constant c. hence;
X2 +10x+c is a perfect square.
Therefore, (10x+2)2 =c
→ c = 25
Thus 25 must be added to x2 +10x to make it a perfect square. If the square base is to be divided by the mass of the chamber, its Top and the welding beam gadget, we would get eighteen, i.e. 450/25. Thus we will need to make the square base at least 18 times larger than the whole width of the chamber for assured stability.
Weight of the chamber and the Top
In order to determine the design for the top of the chamber, certain features have to be considered. For one, the weight of electronic welding equipment plus that of the Top itself should surpass the internal pressure of the chamber to prevent it being blown off since it becomes the object in the air, W1 when the chamber is in use. However, since the top will be as well in direct contact with internal pressure, it can be treated as an object partially immersed in vapour. This shall be W2. For conceptualization purposes, we can treat the vacuum chamber as an empty beaker, since its internal pressure was reduced to make it an almost pure vacuum. We shall then label it W3. However to determine the pressure to be exerted by the Top plus the electronic beam machine, we find out the weight of the pressure displaced. Consequently, we take the weight of the beaker plus the displaced pressure to give us W4. Still done, all these would not complete the work if we did not know the weight of the two, i.e. the cover and the electronic devise on top when totally subjected to internal pressure, W5 (Korchagin, Lavruk, Fadeev, Bardakhanov, Suknev, Larina, and Bogdanov, 2005).
At this level then, we can, with fair ease, be able to tell what amount of pressure and weight we need to deploy in coming up with the appropriate weight of the chamber:
Object partially subjected
Apparent loss in weight=W1-W2
Weight of pressure displaced= W2-W3
Object totally subjected
Apparent loss in weight=W1-W5
Weight of pressure displaced=W6-W3
Observations and conclusions
The object here stands for anything found on top of the vacuum chamber. When the object is partially subjected, that is the mass of both the cover and the beam equipment on the chamber, the apparent loss in weight (W1-W2) equals the weight of pressure displaced (W1-W3).
Similarly, when the object is totally subjected, the apparent loss in weight is thus: (W1-W5)
The results above are a verification of the Archimedes’ principle which states that when a body is totally or partially subjected to pressure, it experiences an upthrust equal to the weight of the pressure displaced. Therefore we can say that if the total weight of the Top plus the electronic beam machine is to be 450kg, then the internal pressure must be less and calculated by the above procedure. This weight of 450kg would have been determined by the pressure we would have found in the chamber, and how much we would have wanted to lose in order to have 450kg as the total amount of weight suitable to be on top.
Note, however, that as we saw in the reaction of metals and vapour, the Top and welding devise materials must not be porous, soluble and or one that can react with any liquid, if need be to have a liquid used.
So far we have been able to discuss and determine the base of the whole chamber, the chamber itself and the Top and beam equipment considered together. However, it will be important to also consider the Top (or cover) itself.
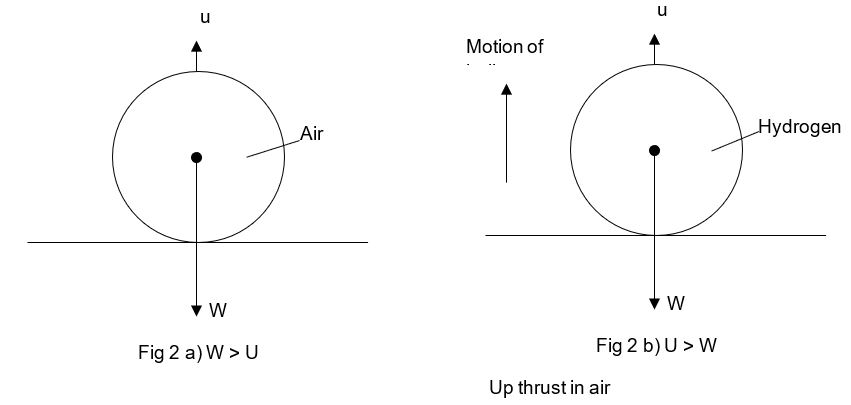
To begin with, we must acknowledge that just like it will happen with liquids, gases exert upthrust on objects in them. The upthrust in air is small owing to its low density. (About 1.3 kgm-3), but sufficient to make light items light items like balloons filled with hydrogen (density about 0.09 kgm-3 or helium (about 0.18 kgm -3) rise.
The figures below illustrate this fact. Consider figure2 below. If it is inflated with air to a certain volume, the weight of air in the balloon plus its fabric is greater that the weight of the air displaced by the balloon, since the volume of the air in the balloon is nearly equal to the volume of the air displaced.
Upthrust on the balloon due to the air is thus less than the weight. The balloon stays on the ground due to the downward resultant force, W-U.
Applying the same principle to our cover on the chamber, we can determine to know how the weight of the Top should go. In the case of the inflated balloon, the weight of the air in the balloon plus the fabric of the balloon was greater than the weight of the air displaced by the balloon since both volumes were nearly equal. This implied the stagnancy of the balloon since the resultant force was downward. However, for our Top, threes no inflation and therefore the only force applicable is that of its fabric and of the electric devise upon it. Therefore the downward thrust will come from the welding machine and the cover while the upward thrust will come from the chamber. To maintain stability therefore, we must seek a way to retain a downward resultant fo2ce, such that the chamber and everything stands firm on their squarer base. To achieve this however the chamber has already been relieved of its internal pressure and converted into an almost pure vessel. This translates into a balloon that has been inflated with a light gas like helium or hydrogen. These should have allowed the balloon to fly off. However in the experiments discussed, only air was filled in the balloon and not these particular gases. Thais implies that if he balloon had been inflated with the low density gases they would need an extra force on them to retain them on the ground. This is because the sum of their fabric and the density in them would be lighter than the atmospheric pressure and thus an upward thrust would have been inevitable. This extra mass in our case should be the weight of the cover and the welding beam equipment. That would mean, the450 kg of their sum weight should surpass that of the chamber and any gases in it. So the chamber and its content must be less than 450kg, in fact by far in order to retain downward thrust and stability of the chamber.
Application of the energy from chamber to welding beam
In our assignment, we have theoretically positioned the electronic beam used for welding on top of the lid or the Top. As such, whatever form of energy that will be stored in the chamber will have to travel in different forms to the beam above. This brings in the question of energy transport by EM waves.
Electromagnetic waves carry energy, as do always. Most industrial sources of energy are driven from electromagnetic energy waves from the sun. Hydroelectric power plants rely on the sun to evaporate water, in a sense pumping it back up hill so that it can again flow down rivers and turn turbines. Wind can be harnessed to generate electricity, but the winds are driven by uneven heating by the sun. The only energy sources we have that do not come from the suns EM radiation a nuclear fission and geothermal energy. This has a relation for our interest.
Energy Density
This reflects the flow of energy from the vacuum chamber to the top where it is to be used by the welding beam machine. The energy is stored in the oscillating electric and magnetic fields in the wave. For a EM vacuum, the energy density (SI unit: J/m3) are
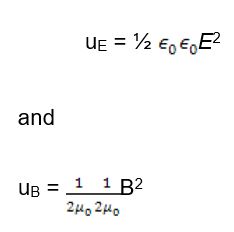
It can be proved that the tow energy densities are equal for an EM wave in vacuum using the relationship between the magnitude of the fields thus for the total energy density we can write.
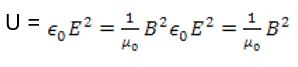
Since the fields vary from point to point and also change at time, so do the energy densities. Since the field oscillate rapidly, in most case we are concerned with the average energy density – the average of the squares of the fields. Recall that rms (root mean square) value is defined as the square root of the average of the square.
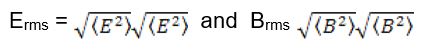
The angle brackets around a quantity denote the average value of the quantity. Squaring both sides we have
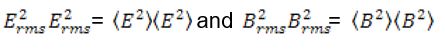
Then the average energy density can be written in terms of rms values of the fields:
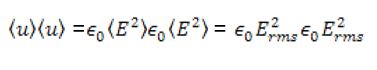
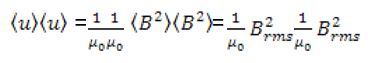
Therefore, we can, in the final analysis, be able to determine what energy can be moving from the vacuum chamber to the welding instrument and at what speed. This will in turn determine the power with which the welding beam will be working. Moreover, the strength with which the welding beam will be working will also determine the kinds of works it will be able to accomplish. Certain metals are certainly harder to burn than others depending on their melting points. Therefore, depending on the purpose the beam is to serve, we could regulate the energy transfer from the vacuum chamber to the point of consumption.
Conclusion
As we have noticed in the discussion, the design and construction of the Top to the vacuum chamber has more to it than that shape and form. For this electronic device to function appropriately, it was necessary that all the aspects, especially the dimensions ha d to be factored in. such include types of metals and their reaction to different substances. Also important were the mass, weight, volume and velocity of the various elements involved. If any of such requirements was flouted at the initial stages of design and construction, not only lives would be imperilled, but also destruction of property causing countless damage, since vacuum chambers are a danger enshrined: harmful gases at undue exposure. This is how crucial the task has been.
References
Jovanovic, B. & Rousseau, P. (2002). Moore’s law and learning by doing. Review of Economic Dynamics 5: 346–375. Web.
Korchagin, K., Lavruk, h., Fadeev, S., Bardakhanov, G., Suknev, P., Larina, Z. & Bogdanov, B. 2005 ’Production of silver nano-powders by electron beam evaporation’, Vacuum 77,