Abstract
In connection with the wide possibilities of practical applications, in recent years, methods of obtaining electromagnetic radiation from relativistic electron and positron beams have been intensively developed. Radiation of high-energy electrons in external magnetic fields has a number of attractive properties: high intensity, sharp directivity, polarization, and precisely calculated spectral characteristics. However, with all its positive qualities, synchrotron radiation (SR) could not fully satisfy the ever-increasing requirements imposed on the characteristics of radiation: intensity, spectral range, monochromaticity, and the possibility of promptly adjusting the type of polarization. Radiation that largely satisfies all these requirements is obtained by passing relativistic charged particles through an undulator. The undulator emits electromagnetic radiation generated by the oscillatory motion of fast charged particles. The paper discusses the possibilities of undulators; the characteristics of various types of undulators, their advantages and disadvantages, as well as directions for further developments in this area are given.
Introduction
At present, in almost all spheres of human activity, the achievements of atomic and nuclear physics are used, which were rapidly developed in the second half of the 20th century. The impetus for this was the emergence of nuclear physics and electrodynamics at the end of the 19th century, and then their development at the beginning of the 20th century [1]. After the discovery of X-ray radiation in 1895, humanity received a powerful tool for investigation of the properties of micro-objects and studying the possibility of their use in science and technology. Interest in the processes occurring during the passage of charged particles through amorphous and crystalline structures remains heightened both among theoreticians and experimenters at the present time. This is due to the general progress of physical research, which stimulated the formulation of a number of problems to discover new effects in the physics of electromagnetic processes. In addition to scientific interest, the practical use of a number of characteristics of electromagnetic processes in crystals is very promising in modern physics.
The search for new sources of intense electromagnetic radiation in different wavelength ranges has contributed in recent decades to the development of theoretical and experimental studies of various types of electromagnetic radiation by relativistic electrons in matter and in external fields. On the other hand, a number of problems can be significantly simplified by using monochromatic radiation, which can be obtained by choosing conditions suitable for the formation of the spectrum, for example, those under which a particle or an electromagnetic field carried by it experiences strictly periodic effects from the substance or an external field. One of the most promising directions today is the monochromatization of synchrotron radiation (SR). Synchrotron radiation is the one that occurs when a particle is deflected from a straight path by a magnetic field. This deviation occurs, in particular, in synchrotrons – cyclic accelerators of high-energy particles. SR has recently become the most important tool for studying the properties of matter and is used today in almost all areas of modern science. Among the main elements of modern SR sources, there are undulators and wigglers – periodic magnetic structures.
In recent years, the direction of creating cavityless (single-pass) X-ray lasers has begun to develop intensively, which in their characteristics (brightness, peak power) are orders of magnitude better than modern sources of synchrotron radiation. Installations of this type require the creation of undulators several hundred meters long with high requirements for periodicity, with a large amplitude and a small spread of the magnetic field. Therefore, the problem of finding new undulator circuits that will allow obtaining high amplitudes of magnetic fields and will also provide focusing of the electron beam in both transverse planes along the entire length of the magnetic system has become acute.
Principal of working with technical details and formulas
Among the various types of undulators, the ones with alternating magnetic fields are the most widely used. A schematic representation of such an undulator and the trajectory of a particle moving in it are shown in Fig. 1.
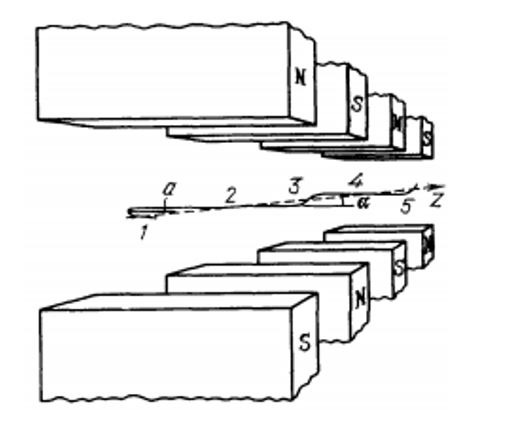
The undulator consists of two periodic systems, each of which contains a large number of magnetic poles of alternating polarity. The strength of the transverse magnetic field of the undulator varies along its z axis according to a law close to sinusoidal with a period λ0. A relativistic particle entering the undulator at a small angle α to its axis is exposed to the magnetic field of the undulator, which leads to the curvature of the initial trajectory of the particle. If the initial conditions at the entrance of the particle into the undulator are selected appropriately, then the particle at each oscillation will cross the axis of the undulator every time at the same angle αm. The value of this angle will be an important parameter; thus, the particle will move relative to the undulator axis along an almost sinusoidal trajectory with a period λ0. Since the force acting from the side of the static magnetic field on the particle is always directed normally to its velocity and the radiation losses are negligible, then during motion in the undulator under consideration the absolute value of the particle velocity, like its energy, is conserved. If the velocity ν is constant, the lengthening of its path caused by transverse oscillations relative to the undulator axis will lead to a certain decrease in its average velocity along the undulator axis νII = cβII in comparison with its absolute value ν = cβ.
Thus, in an undulator, a particle moves along a curvilinear trajectory with variable acceleration in sign and magnitude, and, therefore, emits electromagnetic radiation. The magnitude and orientation of the electric field vector of this radiation are determined by the magnitude and direction of acceleration. With a periodic change in acceleration, the electric field of undulator radiation will also be a function that is periodic in time. It should be noted that in general this function will not necessarily be harmonic.
Speaking about the influence of the parameters of the electron beam and the diaphragm of undulator radiation on its properties, it should be said that each particle of the beam is assigned a point in the six-dimensional phase space, the position of which is set by the transverse coordinates x, y, angles (x’, y’) formed with the undulator axis, the longitudinal coordinate z relative to the center of the beam, and the deviation of its energy from the mean. As a rule, this distribution can be described by a Gaussian law with variances:
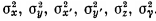
The emittance in a given plane of motion is defined as the product of the standard deviations of the displacements and angles of the particles relative to the beam axis
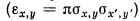
In this case, it is assumed that the center of the beam is always located on the axis of the undulator.
The experimentally observed characteristics of the UR (differential or integral) are determined, in addition to the beam parameters, also by the acceptance of the installation: the shape of the inlet and its dimensions rх and ry. The angular interval of radiation in the direction of observation, allocated by the entrance hole of the experimental installation, is
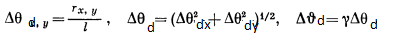
In some cases, it is more convenient to describe the beam parameters by the width of the effective angular distribution at half maximum
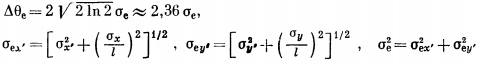
where l is the distance from the center of the undulator to the observation point.
The influence of the beam parameters on the spectral-angular characteristics of undulator radiation becomes noticeable if 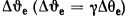
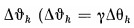
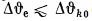
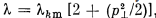
when
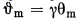
The width of the UR spectral line, taking into account the angular and energy spread of particles in the beam, as well as the angular acceptance of the diaphragm, can be estimated from the expression
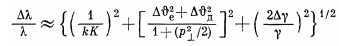
The intensity of radiation propagating at zero angle at a wavelength with the opening of the angle allocated by the diaphragm up to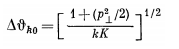
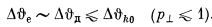
It should be noted that, in the optical region of the spectrum, the separation of monochromatic radiation can also be carried out using a mirror. Requirements for the angular size of the mirror are specified by the same conditions (4). Hence it follows that in a number of experiments that do not require a very high monochromatization of the radiation beam, undulator radiation can be used without a monochromator.
To generate the induced radiation, the mirrors of the optical cavity are placed on the undulator axis. The accumulation and amplification of spontaneous undulator radiation occurs in the cavity. Its high directivity makes it possible, with relatively small dimensions of the resonator mirrors, to confine the main part of the spontaneous emission energy of a given wavelength. When choosing the geometry of the optical resonator, the diffraction size of the emitter in the undulator is taken into account [2]. Obviously, in this case, in contrast to free space, a discrete set of electromagnetic waves (modes) will be excited. The distance between the mirrors is chosen so as to synchronize electron bunches with optical radiation pulses from neighboring bunches of the beam. Monochromaticity of radiation is determined by the length of the electron bunches.
Experiments carried out at the Pakhra synchrotron at a fixed wavelength (wavelength 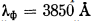
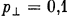
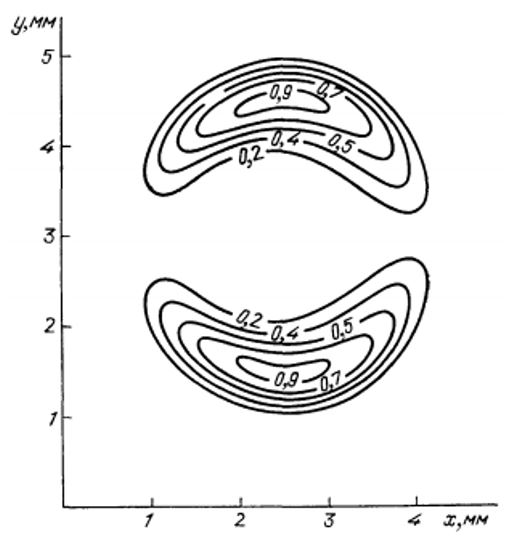
The figure shows that with increasing wavelength, two maxima appear in the distribution of undulator radiation, the distance between which gradually increases.
Specifications
According to the method of creating a magnetic field, undulators are divided into electromagnetic (including superconducting) and permanent rare-earth magnets, which, in turn, are subdivided into iron-free and hybrid ones. The greatest interest and widespread use in recent years, both from the point of view of the maximum achievable amplitude of magnetic fields and the simplicity and compactness of the design, is characteristic for undulators based on permanent rare-earth magnets and, in particular, plane hybrid undulators with vanadium permendur poles [4]. For the technical realization of periodic fields in undulators, EM, SC and PM technologies are used. Fig. 3 shows a comparison of the peak field of undulators using EM, SC and PM technologies.
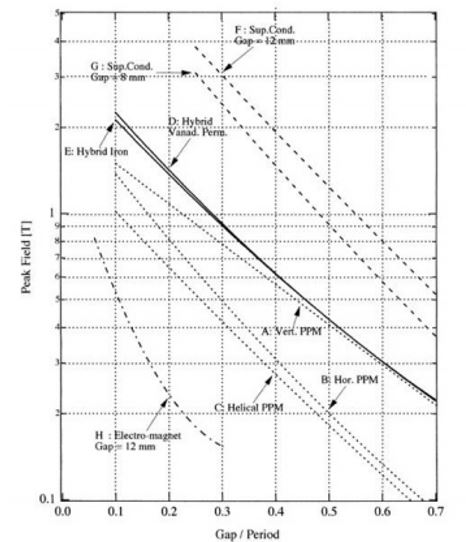
SC provides the highest fields. At a gap of 12 mm a period length of about 50 mm would result in almost 4 T and at a period length of 17 mm still about 0.5 T is possible [4]. EM technology appears appropriate for undulators with long or even very long period lengths, 0 > 200 mm, and for very special applications. This technology is well defined and has many common features with classical EM magnets for accelerator applications.
In recent years, there has been an active search for new accelerator schemes with a high acceleration rate. One of the most promising schemes is a vacuum laser accelerator of the Inverted free-electron laser FEL (IFEL) type, which allows one to obtain both a high acceleration rate and a large percentage of electrons captured in the accelerating process. IFEL is based on the interaction of electron and high-power laser beams in a special undulator [5].
As it is known, there are several methods that allow obtaining a detailed picture of the field inside a magnetic element (devices based on nuclear magnetic resonance, Hall transducers, measuring coils, vibrating wires, etc.) and methods for determining the integral characteristics of magnetic elements (extended integrating coils and longitudinal wires, pulse wire method). It is shown that for tuning magnetic undulators it is advisable to use two methods: for precision measurements required to adjust the amplitudes of magnetic fields, it is best to use Hall sensors; and for the final integral adjustment of the fields, which allows adjusting the trajectory of the electron inside the undulator, it is better to use the pulsed wire method [5].
The Hall transducer method is one of the most accurate and reliable methods. Field measurements are made step by step with stops of the sensor carriage at the measuring points and take a long time. The wire-wound method for measuring magnetic fields is less accurate, but has its advantages. First, it is significantly faster. Secondly, it is more compact and can be used to measure magnetic fields in narrow gaps within the entire undulator. Third, it provides direct information on the first and second integrals of the magnetic field, excluding numerical integration errors. The principle of the method is as follows: a current pulse is passed through a thin wire stretched along the undulator axis (Fig. 4). Under the action of local transverse Lorentz forces, a disturbance region is formed, which propagates in both directions with an acoustic velocity of ~ 300 m/s [6]. An optical sensor located near the beginning of the undulator measures the deflection of the wire, which is proportional to the first or second integral of the magnetic field, depending on the duration of the current pulse.
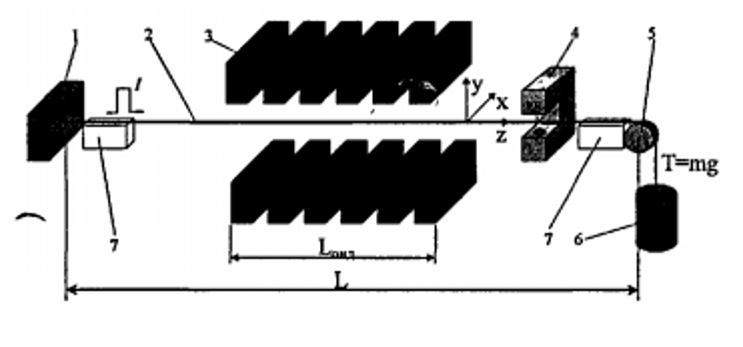
Both of these methods have been significantly improved in recent developments. A high (0.1 Gauss) accuracy of magnetic field measurements was achieved in the test bench based on the Hall sensor. The pulsed wire method was modernized for measuring the fields of extended (> 1 m) undulators and checking their focusing properties [6].
The latest developments of undulators, in contrast to standard ones, focus the electron beam not only in the vertical plane, but also in the horizontal one. This property simplifies the problem of focusing electron beams in FELs, especially in hybrid undulators, at generating electromagnetic radiation in the millimeter wavelength range, when noticeably diverging low-energy electron beams are used, as well as when generating short-wavelength radiation in single-pass FEL circuits, where high efficiency is required for interaction of an electron beam and an electromagnetic wave at relatively large longitudinal distances.
Mention should also be made of the use of modernized methods for measuring magnetic fields to tune real undulator designs, in particular, the use of improved Hall and wire methods for measuring magnetic fields to tune real undulator designs, as well as the results of physical experiments using them.
For a prototype maser with a tunable frequency of megawatt power with high efficiency for the Dutch FOM Institute of Plasma Physics, a two-section stepwise profiled hybrid undulator was designed, assembled and tuned [7]. The specific requirements of the project did not allow using the undulator of the standard circuit. An especially serious requirement is a strong magnetic field exceeding the Halbach limit at a relatively large ratio of the undulator gap to the period of the undulator (0.65 and 0.73 for the first and second sections, respectively). In addition, high requirements were imposed on focusing a high-power electron beam in the energy range from 1.75 to 2.0 MeV. The electron beam loss at a current of 12 A should not have exceeded 0.2%. These requirements have been met. A photograph of the assembled undulator and its section are shown in Fig. 5. The main parameters of the manufactured undulator are given in Table 1.
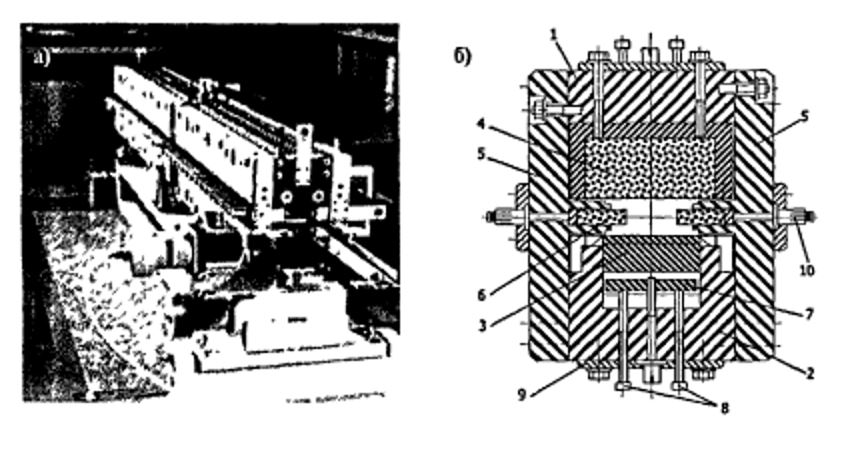
Table 1 Parameters of the electron beam and the main characteristics of the FEL
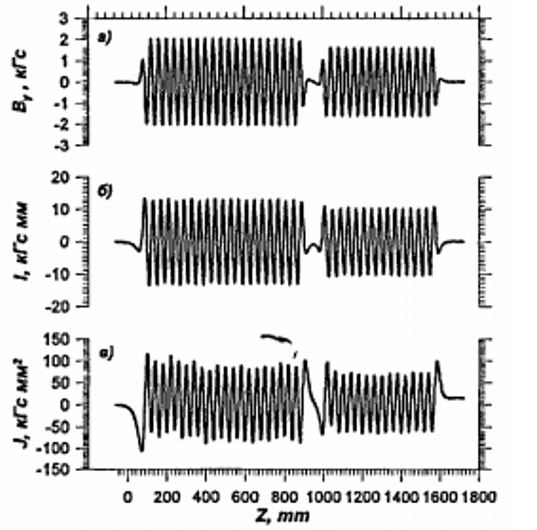
Fig. 6 shows the results of measurements of the magnetic fields of the KIAE4 undulator by the Hall sensor. By individually adjusting the magnetic field of each pole, a very high degree of homogeneity was obtained – the spread of the magnetic field amplitudes did not exceed 0.2%. The contribution of high harmonics to the field shape was less than 0.25% for the third harmonic and less than 0.1% for the fifth harmonic. The relative spread of the amplitudes of the second field integral from the mean does not exceed 10% [8].
Many theoretical works have been devoted to the problem of creating an accelerator with a high acceleration rate since the 1960s. The most promising are laser accelerators. It was shown that it is possible to accelerate electrons by tens of MeV (from 14 MeV to 50 MeV) in an undulator 50 cm long. In this case, in principle, a high electron capture coefficient during the acceleration process (up to 30%) can be ensured [9]. The calculated parameters of such an accelerator are presented in Table 2.
Table 2 Calculated parameters of the laser accelerator
A Gaussian laser beam has a relatively short Rayleigh length (3.6 cm); therefore, the electric field of the driver laser varies greatly along the length of the undulator, reaching a value in the focal region at the center of the undulator.
Comparison of different models and their applications in real life
Advantages and disadvantages
According to the method of creating a magnetic field, undulators can be divided into electromagnetic (including superconducting) and permanent magnets. Electromagnetic undulators differ from other types of undulators: the ability to change the field strength by simply changing the current in the windings; high field uniformity (which is especially important for long undulators). The disadvantages of electromagnetic undulators include the following: relatively complex designs; large heat losses; the complexity/impossibility of fine tuning the magnetic field, which is practically necessary for the passage of the electron beam through the undulator.
Ordinary (warm) electromagnetic undulators, widely used in accelerator technology, can no longer satisfy the requirements for the field strength, for at least two reasons. First, saturation effects will noticeably affect the steel core with an increase in the field, since the magnetic field strength at the pole edge is 1.5–2 times higher than the field on the undulator axis. Secondly, the space between adjacent poles decreases with a period and the required current density in the electromagnetic coils reaches values of the order of 2 kA/cm or more, exceeding the permissible limit for warm electromagnets. In superconducting undulators, there is also a critical current density of the order of 2.7 kA/mm2, but this is two orders of magnitude higher than the limit for conventional warm electromagnets. Relative simplicity of design; lack of additional equipment (powerful current sources, cooling systems, etc.); possibility of fine adjustment of magnetic fields also should be mentioned [10]. Rare earth magnets significantly outperform other permanent magnets in a number of characteristics and especially in terms of remanence.
Rare-earth magnets made of NdFeB alloy have very high remanent magnetization (up to 1.47 T), but a small maximum operating temperature, while magnets from the Sm2Coi7 alloy retain their characteristics (Br up to 1.2 T) at significantly higher temperatures (up to 250ºC). When choosing rare-earth magnets for the designed undulator, one should be guided, first of all, by the temperature conditions in which the device will operate, and only secondarily by their magnetic properties. One of the main drawbacks of the permanent magnet undulator design is a large spread in the magnetization force and direction in different magnetic blocks. To reduce the spread, one has to make a careful selection of magnets, combinatorially group them into pairs, fours, etc. By their design, permanent magnet undulators (PM) are subdivided into pure rare-earth (iron-free) and hybrid [10]. Undulators of this type are the simplest to design and manufacture, but require a computer calculation of the location of preliminary carefully measured magnetic prisms.
The fields adjustment is very difficult (it is practically impossible) and the amplitudes of the magnetic fields of such undulators are small. Substantially stronger magnetic fields can be achieved with the so-called hybrid configuration. Since the pole pieces in the hybrid circuit are usually in saturation, changes in the magnetic field caused by inhomogeneities in the magnetization of the rare earth magnets are reduced. It becomes an option to fine-tune the field of an individual pole using shunts, which makes it possible to achieve high field uniformity.
Future improvements and future research opportunities
The high requirements for undulators in modern coherent radiation devices and the growing demand for sources with specified radiation characteristics have revived interest in the study of the theoretical aspects of UR. The developed mathematical apparatus of extended and generalized forms of special functions made it possible to accurately describe the effect of the finite size of the electron beam, its divergence, energy spread, the effect of non-periodic components of the magnetic field on the intensity, spectrum, and shape of spectral lines of the UR. In particular, the influence of the length of the undulator on all characteristics of the URI was calculated analytically, taking into account the losses, and the possibility of compensating the divergence of the electron beam with a suitably configured constant magnetic field was shown.
At present, sources of undulator radiation find practical application in research in vacuum ultraviolet radiation and in the harder regions of the spectrum, where there is a shortage of intense tunable sources of electromagnetic radiation. There are already interesting results of their application in research on X-ray fluorescence elemental analysis, nuclear spectroscopy, medical diagnostics, and spectroscopy. In the near future, it is planned to further increase the radiation power of operating lasers and place them on a third-stage FEL with wavelengths in the near infrared range of 5-30 microns [11]. There are always many plans in this interesting and promising field of knowledge.
There is no doubt that their use will become more widespread in the near future. For example, in all projects of specialized SR sources being implemented and developed to date, the undulator becomes an essential element. The presence on the largest proton synchrotrons of intense beams of high-energy monoenergetic electrons (tens and hundreds of gigaelectronvolts) and the creation of colliding electrons in the near future; positron beams with energies up to 100 GeV will allow, when they are decelerated in an undulator, to generate intense fluxes of polarized quasi-monochromatic photons of high energy (of the order of several megaelectronvolts and above) [12]. Such photons are of independent interest for the production of polarized electrons and positrons in linear colliding electron-positron beams and for research in the field of photonuclear physics and high-energy physics.
Using radiation from a spiral undulator installed in an electron-positron collider, it is possible to obtain fluxes of monochromatic circularly polarized photons arising from Compton scattering of undulator radiation from one of the beams on a counterpropagating beam. The energies of such photons will be close to the energy of the colliding particles. From their angular distribution, one can judge the polarization of the electron-positron beams.
Modern physics formulates topical problems, the solution of which leads to the need to create new tools for collecting information and its subsequent analysis. One of these tools, of course, are the sources of powerful radiation in the X-ray range, which make it possible to operate on various phenomena at the atomic and molecular level; in fact, without this class of devices it is impossible to imagine the study of submicron and nanosystems [12]. Particular attention in the class of the described radiation sources is paid to FELs, which differ in a wide range of operating frequencies, up to soft X-ray ones (at present, it is planned to obtain harder radiation in FELs under construction), coherence and polarization of the output radiation.
Free electron x-ray lasers (FELs) have opened new horizons for researchers. It became possible to study the chemical and physical properties of substances, for example, exotic crystalline structures of nanomaterials, where high radiation power is important, and thanks to the coherent properties of FEL radiation, one can “see” electronic transitions in little-studied quantum systems with short-lived states, and much more. For one of the largest and most powerful X-ray FELs in the world, the European X-ray Free Electron Laser (XFEL), the possibility of an ultrafast change in the polarization of the FEL radiation was simulated.
References
B Lai, Khounsary, A, Savoy, R, Moog, L, and Gluskin, E. Undulator A characteristics and specifications. United States: N. p., 1993. Web.
A. V. Korol, A. V. Solov’yov, and W. Greiner. Channeling and Radiation in Periodically Bent Crystals. UK, London: Springer, 2014.
N. A. Vinokurov and E. B. Levichev. “Undulators and wigglers for the production of radiation and other applications,” Physics Uspekhi, vol. 58, no. 9, p. 850-871, 2015.
C. Pellegrini, A. Marinelli and S. Reiche, “The physics of x-ray freeelectron lasers.,” Rev. Mod. Phys., vol. 88, pp. 15-26, 2016.
J. Pflueger. “Undulator Technology,” Proceedings of the CAS-CERN Accelerator School: Free Electron Lasers and Energy Recovery Linacs, Hamburg, Germany, 2016, edited by R. Bailey, CERN Yellow Reports: School Proceedings, Vol. 1/2018, CERN-2018-001-SP (CERN, Geneva, 2018).
B. A. Peterson et al. “Technology development for short-period magnetic undulators.” Physics Procedia, vol. 52, pp. 36-45, 2014.
K. Kim, Z. Huang and R. Lindberg. Synchrotron Radiation and Free-Electron Lasers: Principles of Coherent X-Ray Generation. Cambridge: Cambridge University Press, 2017.
K. V. Zhukovsky. “Generation of X-Ray radiation in free-electron lasers with two-frequency undulators.” Optics and Spectroscopy, vol.60, pp. 1630-1637, 2018.
J. Bahrdt J. Shaping Photon Beams with Undulators and Wigglers. In: Jaeschke E., Khan S., Schneider J., Hastings J. (eds) Synchrotron Light Sources and Free-Electron Lasers. Springer, Cham., 2019. Web.
S. Yamamoto. “Development of undulator magnets towards very short period lengths,” AIP Conference Proceedings 1741, 020029 (2016); Web.
A. Schops et al. “Recent undulator developments at DESY.” Journal of Physics Conference Series, vol. 425, no. 3, 2013. Web.
S. Fisher and C. Roques-Carmes. “Monochromatic X-ray source based on scattering from a magnetic nanoundulator,” ACS Photonics, vol. 7, pp. 1096-1103, 2020.