Adsorption is the capacity of all strong substances to pull to their surface atoms of gases or arrangements with which they are in touch. Solids that are utilized to adsorb gases or break down substances are called adsorbents. Regularly, adsorbents have little pore widths so that there is a high surface region to work with adsorption. The pore size normally goes somewhere in the range of 0.25 and 5 mm (Do, 1998). Mechanical adsorbents have high warm steadiness and protection from the scraped area. The surface of mechanical adsorbents can be either hydrophilic or hydrophobic. Adsorbents can be characterized by a variety of shapes (including but not confined to pellets and poles, as well as formed shapes).
Other adsorbent materials might be utilized in nonwoven channels: alumina, silica gel, actuated carbon, and zeolite. Alumina is an aluminum oxide that is exceptionally permeable and displays a gigantic surface region. Alumina is such a functioning adsorbent that it adsorbs water from encompassing air whenever offered the chance. Silica gel is an artificially dormant, non-harmful, polar, and dimensionally steady (< 400 °C or 750 °F) nebulous type of SiO2. It is ready by the response between sodium silicate and acidic corrosive, which is trailed by a progression of after-treatment cycles like maturing, pickling, and so forth. Initiated carbon adsorption genuinely connects gas or fluid-stage particles to the outer layer of the actuated carbon. It is a compelling adsorbent since it is a profoundly permeable material and gives a huge surface region to which foreign substances might adsorb.
Actuated carbon contains carbonaceous material that is received from charcoal. It is delivered by pyrolysis of natural materials of plant beginning. Actuated carbon has great potential for adsorbing substantial metals as a result of its more noteworthy surface region, microporous capacity, and compound intricacy of its outer region. Zeolite is a viable permeable and adsorbent apparatus in eliminating hydrocarbons, radioactive cations, smelling salts, and weighty metal cations in mechanical conditions. Zeolite additionally dominates in squandering the board and remediation arrangements.
In Gibbs’ thermodynamic hypothesis of surfaces, the overall conditions overseeing balance at interfaces were given, including conditions administering adsorption. Gibbs’ most broad conditions apply to any conceivable situation of this surface. However, the specific condition, usually known as “Gibbs’ adsorption condition,” was found by the guide of a specific decision of the situation of this numerical surface, with the end goal that the surface abundance of one of the parts disappeared.
Adsorption can happen as a result of actual powers or by substance bonds. It is generally reversible, which implies it is dependable for the deduction of substances as well as for discharge. In the majority of the cases, this cycle is depicted at the balance through certain situations that measure the measure of substance appended on a superficial level, given the focus in the liquid. These conditions are called isotherms as a result of the reliance of their boundaries on the temperature, which is perhaps the main ecological factor influencing adsorption. The most well-known isotherms are the Langmuir and the Freundlich conditions.
The Langmuir adsorption model clarifies adsorption by accepting an adsorbate acts as an optimal gas at isothermal conditions. At the point when the measure of adsorbed particles per unit space of the interface is plotted as an element of either the balance pressure or the balance arrangement fixation at a steady temperature, the acquired bend is called an “adsorption isotherm.” If the collaborations between the adsorptive areas are more grounded than those between the adsorptive surface and the iotas on the substrate, the adsorptive areas tend to group together to limit their contact with the substrate. The got film is island-like, and after the continuation of the testimony cycle, the islands will complete combining to frame a diverse film, absolutely covering the substrate.
At something contrary to the past circumstance, when the collaborations between the adsorptive areas and the substrate are a lot more grounded than their intermolecular communications, the adsorptive surface structure of a monolayer on the substrate, and the development cycle can be captured at this level. The adsorbent surface viable is described by four kinds of adsorption focuses, which vary in the measure of energy focus. The Langmuir condition is determined around the monolayer being the restriction of adsorption, though the BET condition models halfway and multi-facet adsorption as far as the monolayer.
The Freundlich condition is an adsorption isotherm and an experimental connection between the amount of gas adsorbed into a strong surface and the gas pressure. A similar relationship is additionally appropriate for the grouping of a solute adsorbed onto a strong’s outer layer and the solute’s convergence in the fluid stage. Brunauer, Emmett, and Teller (BET) determined the main isotherm for multi-facet adsorption. It expects an irregular dispersion of locales that are vacant or that are covered with one monolayer, two layers, and so on. The framework is grounded on the assumption that the adsorption rate of any layer equals its desorption rate. The equation for the first layer’s adsorption and desorption rates is as follows:
a1Ps0 = b1s1 exp
In this equation, E1, a1, and b1 are independent of the adsorbed amount and constant. E1 stands for the interaction energy between the first-layer molecule and the solid, and it is expected to be higher compared to vaporization heat. The same equation can be drawn to any layer, and it will be written as follows:
aiPsi-1 = bisi exp
The total area equals the sum of individual areas, which can be formulated in the following way:
The adsorbed gas volume covered by one layer is the fraction with one layer of molecules multiplied by the coverage of monolayer Vm. The total volume of adsorbed gas at a particular pressure equals the sum of all volumes, which is represented in the following equation:
= Vm
Hence, the BET surface region is estimated by the explicit surface space of the adsorbent. It is estimated by utilizing non-destructive gases like N2, CO2, Argon. BET surface region relies upon the size and number of gas atoms adsorbed. The equation given above can be simplified with the use of such parameters as P (pressure) and C that is calculated as a fraction between the rate consonants of the second and following layers and reduced heat of liquefaction. Based on this simplification, the BET equation is formulated as follows:
The BET equation can be illustrated with the help of Figure 1.
It is assumed that the temperature of the first layer is equal to the following layer at infinite temperature, which makes it possible to calculate the interaction energy between the solid and the first layer if C is known. This interaction energy is always greater as compared to adsorption heat, so C is usually more than 100.
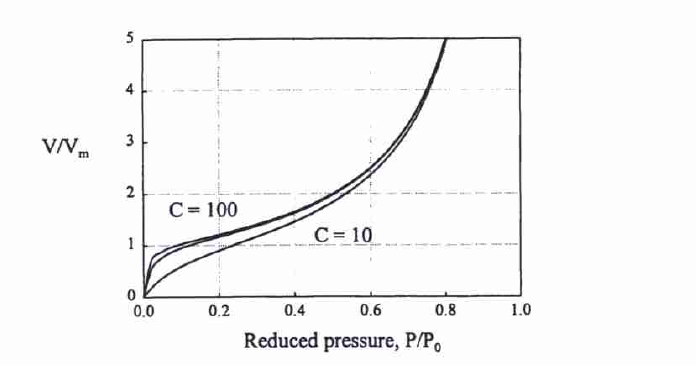
BET Equation Properties
The analysis of the slope and inflexion points suggests that the slope grows with an increase in pressure, becoming infinite as soon as the vapor pressure is gotten. Thus, the derivative of the BET equation is as follows and can be illustrated graphically (see Figure 2):
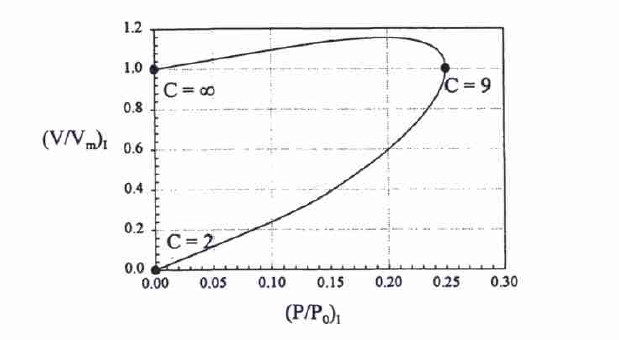
The BET equation is also employed to determine surface area with the known Vm (monolayer coverage) and the known surface area of one molecule. The linear equation, where NA is the Avogadro number, Vm (mole/g), and am is the projected area of the molecule, is as follows:
A = VmNAam
Bet theory describes the multilayer adsorption that can be typified in five isotherm classes (Figure 3).
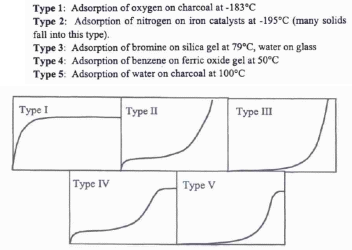
The BET equation for n-layers illustrates the three first types of the isotherm. When C is greater than 1 (which is a common case) and when the vapor pressure is reached, the adsorbed amount can be calculated with the help of the following equation:
Pore Size Distribution
The adsorption cycle encompasses pore filling with adsorbate that occurs in a radial manner, causing the gradual increase in adsorbed amount versus pressure. The BET equation is also employed to calculate the equilibrium between the phases of adsorption. The Kelvin equation is used to determine the pore radius when the condensation pressure, the contact angle, the surface tension, and the molar volume of liquid are known:
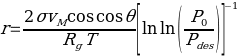
The mean pore radius can be estimated with the help of the following equation:
In Chapter 4, the authors present a relevant adsorption mechanism that is typical of microporous solids exclusively and is referred to as micropore filling. Such solids are characterized by micropore walls that are located close to each other. Dubinin coined the term and provided diverse equations developed to describe the equilibria in such types of solids. The micropore-filling mechanisms were described with the help of zeolite CaA and NaX due to the small (almost insignificant) surface areas of these crystals and large volumes of micropores.
Empirical Data for Volume Filling
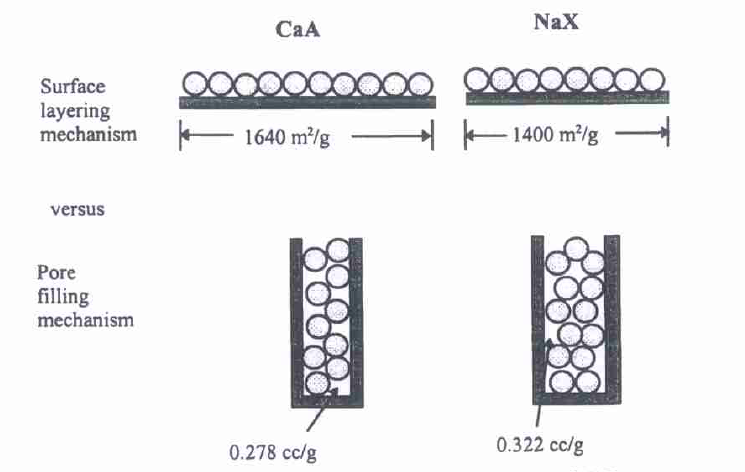
The analysis of the ratios of surface areas, void volumes ratios, and experimental amount adsorbed ratios illustrates the micropore filling mechanisms (see Figure 4).
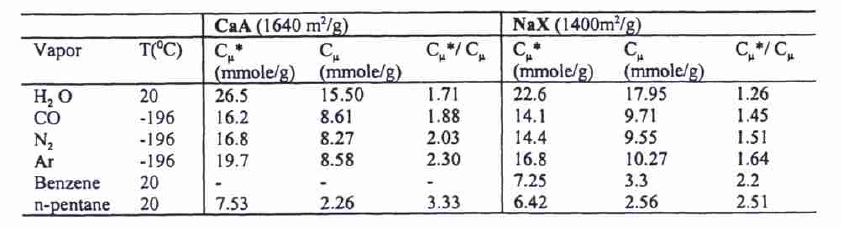
The calculations of the amount in the monolayer adsorption mechanism suggest that micropore filling takes place rather than the mechanism of surface layering. The estimation of the experimental ratio of the adsorbed amount of the 2 zeolites is as follows:
This ratio is in agreement with the void volumes ratio of the 2 zeolites:
While it is not in agreement with the surface areas ratio:
These calculations illustrate the mechanism, which is that of adsorption by micropore filling (see Figure 5).
Adsorption forces include the valence energy force, electrostatic forces, and cohesive energy force. Van der Waals forces referring to the attraction of molecules and atoms can be dipole-dipole, dipole-induced dipole, and dispersion forces. The dispersion force is central to adsorption as this force refers to the generation of dipole that polarizes nearby atoms. The energy of dispersion interaction between molecules or atoms that are identical can be governed by London’s equation:
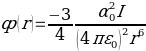
The equation is different for dissimilar molecules or atoms:
In order to calculate the total interactive potential energy emerging between a solid atoms layer and a molecule or atom, the abovementioned equation is summed in terms of pairwise interaction regarding all solid layer atoms.
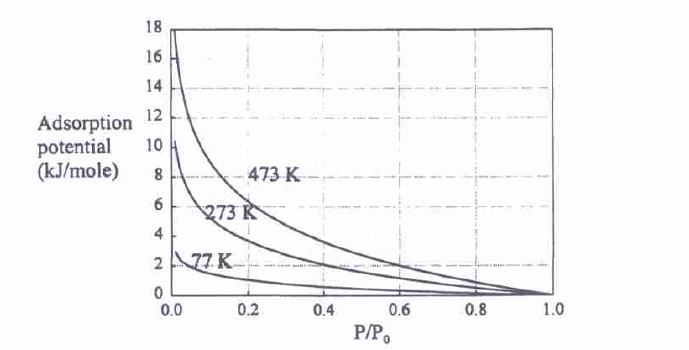
Based on Dubinin’s concepts, the following equations describing micropore filling were developed: Dubinin-Radushkevich, adsorption potential A, adsorbed molar amount, the characteristic curve, Dubinin-Astakhov, and the heterogeneity parameter n. The Dubinin-Radushkevich (RD) adsorption equation is Ɵ = exp[-(A/E)2]. This equation is appropriate for calculations of adsorption at different temperatures as the adsorption potential tends to collapse into a similar curve, called the characteristic curve. The adsorption potential A is a modified Gibbs free energy on adsorption and is formulated as follows: A = -∆Gads. The adsorption potential is high when the reduced pressure is low and vice versa (see Figure 6).
Dubinin equations have also been modified and applied when calculating adsorption isotherms of solids with different characteristics. These equations, however, are inapplicable for the description of adsorption at low pressure. When analyzing such adsorption mechanisms, the following approaches are utilized: Yang’s, Schlunder’s, and modified Antoine equation. The heterogeneity parameter n is employed as a microscopic measurement of microscope size distribution sharpness. The heterogeneity parameter is empirical, and the DA equation is used to calculate it.
Adsorption heat is estimated with the help of van’t Hoff equation:
The isosteric heat is calculated with the following equation:
The adsorption potential (A) is estimated with the following equation:
The sum of the three terms mentioned above is the isosteric heat. The following is the expression of the adsorption isosteric heat in terms of loading:
Reference
Do, D. D. (1998). Adsorption analysis: Equilibria and kinetics. Imperial College Press.