Introduction
Models of asset pricing are ways of mapping from theoretical circumstances of this world into prices of the financial assets such as bonds and stocks. Prices are considered as endogenous to be precise, the world’s circumstances cause them and not vice versa as of asset pricing models.
There are a number of these models which include Arbitrage Pricing Theory (APT), Capital Asset Pricing Model (CAPM), Intertemporal Capital Asset Pricing Model (ICAPM) and Consumption-based models (Lucas) (Beggs, 2011).
CAPM of William Sharpe and John Lintner in 1964 and 1965 respectively marked the beginning of the theories of asset pricing and as a result of this William Sharpe received the Nobel Prize in 1990.
There were no models of asset pricing before their penetration built from the first principles on the nature of investment opportunities and tastes and with logical testable forecasts on return and risk.
For five decades or so, CAPM has been widely used and it is still being used in predicting firm’s cost of capital as well as in assessing portfolio performance (Fama and French, 2003). Thus this paper will discuss CAPM in detail.
Capital Asset Pricing Model
CAPM was derived from the Capital Market Theory where an individual asset is valued instead of a whole portfolio. Risk of that asset is considered the only independent variable that influences the return of a portfolio.
The CAPM function explains the relationship between the risk of an investment and the expected return of the same. CAPM accounts for the sensitivity of the assets to the non-diversifiable risk, occasionally represented by beta (β) and the market’s expected return and theoretical expected return of the risk-free asset (Sharpe, 1999).
Building on earlier research of the Harry Markowitz with reference to Modern Portfolio Theory and diversification, Jack Treynor, William Sharpe, John Lintner and Jan Mossin individually introduced CAPM while Markowitz, Sharpe and Merton Miller together won Nobel Prize for their contribution in the discipline of the financial-economics (Money-zine.com, 2006).
CAPM formula
The model prices a portfolio or individual security; for single assets, security market line (SML) as well as its connection to the beta (systematic risk) or expected return indicate the way the market should price individual assets relative to the risk of their security class.
SML allows investors to determine risk-reward’s ratio of any asset relative to the risk-reward of the general market. Thus, the risk-reward ratio of the individual asset equates to the risk-reward ratio in the marketplace when anticipated rate of return of any asset is deflated (Money-zine.com, 2006). Therefore, CAPM formula is as shown below.
E (Ri) = Rf + β (E (Rm) – Rf)
Where, E (Ri) is anticipated return from the security
Rf is risk-free interest rate for instance interest from treasury bonds
Βi is sensitivity of anticipated surplus security returns to anticipated surplus market returns
E (Rm) is anticipated market return
E (Rm) – Rf is the market premium
E (Ri) – Rf is the risk premium
The anticipated market return is normally determined by using historical returns to calculate Geometric Average such as S&P 500. In addition, historical risk-free returns are used to determine risk premium and not present risk-free return (Sharpe, 1999).
Security Market Line and Asset Pricing
SML explains the CAPM function. The y-axis shows the anticipated return and x-axis indicates the beta (risk). The risk premium is calculated from the SML’s slope; the association between expected return and beta is shown on the SML, which indicates return expected as a beta function.
The nominal risk free rate is the intercept existing in the market, whilst the market premium is the slope. The SML can be considered as representing asset price’s single-factor model, where beta is the exposure to fluctuations of asset value in the market (Money-zine.com, 2006).
SML is a constructive tool used to establish if the security being measured for the portfolio provides a rational anticipated return for the risk.
The SML only plots for an individual asset; in case the asset’s anticipated return versus the risk is drawn above SML, this means the asset is undervalued because the investor may anticipate higher return for inherent risk (Money-zine.com, 2006).
On the other hand, asset plotted below SML is thus overvalued because the investor may be accommodating lower return for assumed amount of the risk exposure. The following diagram indicates the SML, which explains the CAPM functions based on Markowitz portfolio theory, the risk of an asset in a portfolio is the covariance of that asset with the market portfolio m (Money-zine.com, 2006).
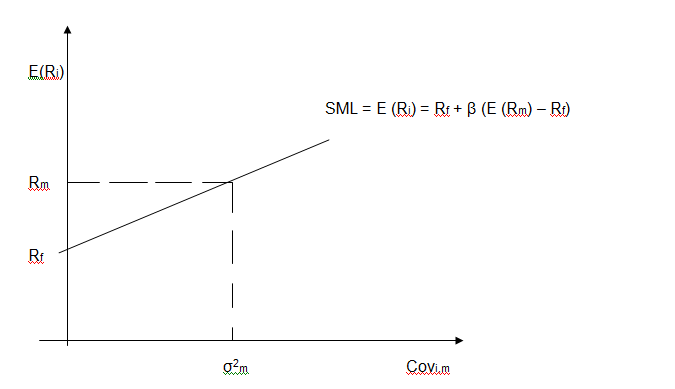
Based on CAPM the risk of an asset is measured by β coefficient and β is a standardized measure of covariance which allows an analyst to evaluate the nature and extent of that relationship with reference to the market portfolio.
For instance, β coefficient of 1.2 can be interpreted to mean that a particular asset is more risky than the market portfolio.
It implies that if the returns of the market portfolio move by 1% relative to the mean then the return of the asset i will vary by 1.2% relative to the mean. The asset return is influenced by the β coefficient since all other variables already exist in the market (Money-zine.com, 2006).
When constructing a portfolio the CAPM calculated return gives us the theoretical value of an asset which means that is what the asset is expected to value and therefore that is the value which will plot the asset on the SML.
However, the economical realities are that the actual price of the asset in the market is determined by market forces of demand and supply for that asset which can price the asset and plot the asset on the SML (Money-zine.com, 2006).
Therefore, in a portfolio construction the best decisions are to buy all the undervalued assets in the market when constructing a portfolio and sell off any overvalued asset currently held when managing a portfolio. This way portfolio will be constructed at a discount price while asset should be sold at a market value.
Thus CAPM, in a portfolio construction gives the minimum return on a security or an asset which should yield or return in order to justify being included in a portfolio (Moneyterms.co.uk. 2011).
Asset-particular required return
CAPM yields a suitable discount rate or required return for the asset that is used to discount projected cash flows from the asset provided by the relative riskiness of the asset. Beta in excess of one indicates higher risk and less than one shows lower risk.
Therefore, a risky security will have higher β and a higher rate will be used to discount it while less sensitive security will be discounted using lower rate since it has lower β. CAPM is constant with intuition provided that the utility function of the investor is concave that is the investors need superior return for investing in asset that is more risky (Sharpe, 1999).
Beta normally reflects the asset-particular sensitivity to the market risk or non-diversifiable risk, thus the market has a β of one as a whole. Indices of the stock market are often utilized as market’s local proxies, and therefore they have a β of one. Any investor investing in a greatly diversified portfolio such as mutual fund anticipates performance in proportion to the market (Valuebasedmanagment.net, 2011).
Diversification
A portfolio risk consists of systematic risk (non-diversifiable risk) and the unsystematic risk (diversifiable or idiosyncratic risk). A systematic risk is the risk that can be found in all the securities that is market risk while diversifiable risk is risk coupled with the individual security.
Systematic risk cannot be diversified in one market but the unsystematic risks may be diversified by investing in a portfolio with large number of securities.
The total number of securities to be included in the portfolio depends on the economy or market; in the developed markets like U.S. and UK a portfolio consisting of about 30 to 40 assets will make the portfolio adequately diversified in that exposure to risk is restricted to only systematic risk.
In the emerging and frontier markets huge amount of assets are required as a result of superior security volatilities (Sharpe, 1999).
Rational investors must not be exposed to any diversifiable risk because only systematic risks are compensated in case of CAPM. Thus, the asset’s return should be related to its risk in the context of the portfolio that is its contribution in terms of risk to the portfolio risk rather than its individual risk.
In the context of CAPM, portfolio riskiness is characterized by superior variance that is less predictable. That is to say the portfolio beta is the essential factor in compensating the non-diversifiable risk taken by the investors (Markowitz, Todd and Sharpe, 2000).
Efficient Frontier
CAPM presumes that portfolio return-risk profile may be optimized; a portfolio that is said to be optimal presents the least likely risk level for its return level. In addition, since every extra security introduced into the portfolio diversifies further the portfolio, an optimal portfolio should consist of every security.
All the optimal portfolios consist of the efficient frontier. Since the idiosyncratic risks are diversifiable, the overall risk of the portfolio may be measured by β (Markowitz, Todd and Sharpe, 2000). The diagram below shows the Markowitz efficient frontier.
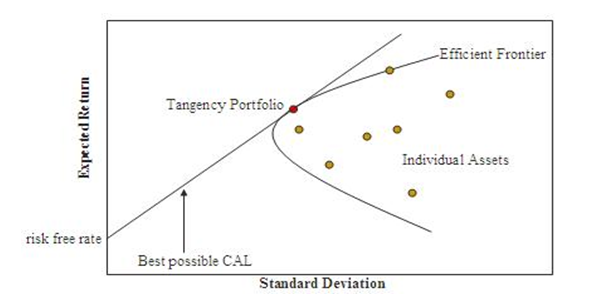
Market Portfolio
Investors may opt to invest the proportions of their wealth in portfolios of risky securities with residue in cash, receiving an interest rate that is risk-free. The investor may opt to borrow cash to finance the purchase of the risky securities wherein there is negative weighting of cash.
In this case, then the risky security ratio to risk-free security does not establish the overall return and thus this association is evidently linear. Therefore, it is feasible to attain specific return by either investing all the investor’s wealth in any portfolio with superior risk or investing a percentage of wealth in any portfolio with superior risk, while the residue is retained as cash.
However, just one of the two portfolios will turn out to be optimal, given the return level and in the perspective of the lowest risk. Because the risk-free security is normally uncorrelated with other security, the second option will in general have the least possible risk and thus be more effective than the first option (Elton and Gruber, 1995).
The association holds also for all the portfolios along the efficient frontier: portfolio with superior return together with cash is efficient compared with portfolio with lower return alone for the same lower return level. In case of a risk-free rate, only one portfolio is optimal that can be mixed with cash in order to attain lowest risk level for any likely return, which is market portfolio (Elton and Gruber, 1995).
CAPM Assumptions
CAPM is developed based on the following assumptions:
- All investors are Markowitz efficient investors and therefore will invest in a portfolio of risky assets along the Markowitz efficient frontier,
- Investors can borrow and lend at the risk-free return rate,
- Transaction costs and taxation do not exist in the capital market therefore there is free flow of funds between assets depending on the yields,
- Inflation is not an important consideration because it does not significantly affect the performance of the portfolio. However, should inflation be an issue it will be effectively dealt with and,
- Investors seek to maximize their single period utility.
Additionally, CAPM presumes that the historical returns standard deviation is an ideal proxy for future risk connected with a particular asset.Under CAPM a portfolio will include both risky and risk-free securities (McCracken, 2009). Therefore, the risk and return of such a portfolio will be measured as follows;
Let Wr be the investor’s wealth committed in the risk-free security
Thus the portfolio return is measured as follows;
E(Rp) = WrRf + (1 – Wr)Ri
Where, Rf and Ri is the average return of the risk-free security and risky security respectively.
While portfolio risk is as follows;
E (σp) = √ ((1 – Wi) 2 x σi2)
Criticisms of CAPM
CAPM has been criticized to have many problems that include; first, CAPM presumes that there are no transaction costs or taxation, and thus if costs do not exist investors will sell or buy mispriced assets plotted below or under the SML.
Second, market portfolio comprises of all securities in all the markets, where every security is weighted through the use of its own market capitalization.
Therefore, this presumes no inclination between securities and markets for single potential and active investors, and that potential and active investors select securities exclusively as their return-risk profile function. It also presumes that all securities are considerably divisible to amount that can be transacted or held (Valuebasedmanagment.net, 2011).
Thirdly, CAPM presumes that all potential and active investors will deem all their securities and optimize only one portfolio. The assumption contradicts portfolios owned by individual investors: people have a tendency of having fragmented portfolios, multiple portfolios and for every objective one portfolio.
Finally, market portfolio must in theory embrace all forms of securities that can be held by any investor like an investment, including, real estate, art and human capital. In reality, that type of market portfolio cannot be observed and investors normally use a proxy such as stock index to replace the real market portfolio.
Unluckily, this replacement has been indicated to be unsafe and may result to false conclusions to the soundness of CAPM and as a result of lack of any real market portfolio, it is alleged that CAPM may not be tested empirically (Valuebasedmanagment.net, 2011).
References
Beggs, J. 2011. Definition of Asset pricing models. Web.
Elton, E. and Gruber, M., 1995. Modern portfolio theory and investment analysis, 5th edition. New York: Wiley.
Fama, E. and French, K., 2003. The Capital Asset Pricing Model: Theory and Evidence. CRSP Working Paper No. 550; Tuck Business School Working Paper No. 03-26.
Markowitz, H., Todd, P. and Sharpe, W., 2000. Mean-variance analysis in portfolio choice and capital markets. New York: John Wiley and Sons.
McCracken, M., 2009. CAPM – The Capital Asset Pricing Model. Web.
Moneyterms. 2011. CAPM. Web.
Money-zine. 2006. Capital Asset Pricing Model or CAPM. Web.
Sharpe, W., 1999. Portfolio theory and capital markets: The original Edition. New York: McGraw-Hill Trade.
Valuebasedmanagment.net. 2011. Capital Asset Pricing Model CAPM. Web.


