Introduction
Osmosis and diffusion are physical processes that scientists in diverse fields such as physical and biological sciences have used in the elucidation molecules’ movement under various conditions. Fundamentally, osmosis is a mechanism in which solvent molecules move from a section that has a lower concentration of solutes to a section that has a higher concentration of solutes through a semi-permeable membrane (Elmoazzen, Elliot, & McGann, 2009). Comparatively, diffusion is a mechanism in which molecules move from a section that their concentration is high to a section where their concentration is low (Zhou, Nyberg, & Rowat, 2015). The aim of the mechanisms in both osmosis and diffusion is to balance the concentration of molecules in two sections so that they can have the same concentration. Therefore, the research paper aims to describe cell membrane osmosis and diffusion in relation to physics.
Cell Membrane Osmosis
Semi-permeability of the cell membrane and the direction of solvent molecules are two concepts that effectively describe osmosis as a physical process. The cell membrane is semi-permeable because it selectively allows water molecules to pass through it and prevents the entry of biomolecules such as proteins, lipids, carbohydrates, and vitamins (Elmoazzen, Elliot, & McGann, 2009). The difference in the concentration of solutes in two sections that the membrane divides forms osmotic gradient, which determines the direction of the solvent molecules. In pharmacy, osmosis is applicable in modulating pharmacokinetics and pharmacodynamics of drugs. For instance, pharmacists employ osmotic drug delivery systems in ensuring that there are optimum absorption and distribution drugs and minimized metabolism and excretion to increase the bioavailability of drugs in the body.
Mechanism of Osmosis
The mechanism of osmosis relies on the concentration of solutes in various solutions. According to the formula developed by Jacobs and Stewart, osmosis is subject to the concentration of solutes and the thickness of cell membrane, which collectively determines the osmotic pressure or osmotic gradient (Elmoazzen, Elliot, & McGann, 2009). Moreover, the integrity of the membrane determines the occurrence of osmosis. Elmoazzen, Elliot, and McGann (2009) explain that the membrane should be semi-permeable for osmosis to occur, which means that it should only be permeable to solvent molecules but impermeable to solutes. The formula developed by Jacobs and Stewart to determine the concentration across cell membrane indicates that:
Concentration gradient = Co – Ci/ l
Where Co represents the concentration inside the cell, Ci represents the concentration outside the cell, and l represents the thickness of cell membrane.
In elucidating the thermodynamics of osmosis, physicists mainly use the osmotic virial equation, which MacMillan and Mayer formulated in 1945. The osmotic virial equation indicates that osmolality of a solution that has a single solute is a function of polynomial molality of solute as indicated by the following equation.
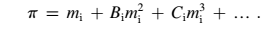
Where π is osmolality, mi is molality, and Bi and Ci are constants of osmotic virial equation
The osmotic virial equation can also determine osmolality of solutions with solutes. According to Elmoazzen, Elliot, and McGann (2009), solutes in a given solution increases osmolality, as the osmolality of multi-solute solutions constitutes the sum of osmolalities of each solute present. However, the determination of osmolality in multi-solute solutions is not direct as there are solute-solute interactions. When a solution has two solutes, named i and j, the cross-constant, Bij, explains the interaction effect of solutes on osmolality.
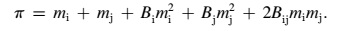
Diffusion
Diffusion is simply a physical mechanism that describes how molecules move from a section where their concentration is high to the section where their concentration is low. Two sections of molecules, which are the section of high concentration and the section of low concentration, create concentration gradient for the molecules to move. In this view, diffusion is essentially the movement of molecules down the concentration gradient. In biological systems, the physiological process of respiration follows the mechanism of diffusion, and thus, allows organisms to exchange carbon dioxide for oxygen. In physics, the movement of gases in a given space effectively demonstrates the mechanism of diffusion.
Mechanism of Diffusion
The mechanism of diffusion is dependent on the concentration of molecules in a given space or environment. The fundamental mechanism of diffusion is that molecules move from a section where their concentration is high to where their concentration is low. The movement of molecules is subject to concentration gradient and electrostatic forces, which ensure there is a net movement of molecules (Zhou, Nyberg, and Rowat, 2015). Concentration gradient initiates and determines the direction of the moving molecules while electrostatic forces sustain the movement of molecules. The movement of gases demonstrates how diffusion of molecules occurs in the air.
In a bid to illustrate the mechanism of diffusion, scientists have come up with different formulas. Boltzmann’s H-function is one of the formulas that scientists use in predicting the process of diffusion. According to Boltzmann’s equation, the distribution of molecules (H) is a function of time moment (t), the position of molecules (x), and velocity of a molecule (dx) (Hubbard, Lund, & Halter, 2013). When two different molecules have the same time moment, position, and velocity, diffusion does not occur. Consequently, the diffusing molecules reach a stationary state or dynamic equilibrium.
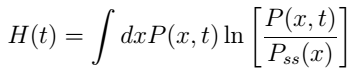
Fick’s laws constitute the basis of the elementary theory that demonstrates how diffusion of molecules occurs. The first Fick’s law predicts that the amount of molecules, which is the diffusion flux (J), have a positive relationship with the negative concentration gradient (D), concentration gradient (dC), and negative relationship with the distance (dx) (Zhou, Nyberg, & Rowat, 2015). In essence, according to the Fick’s laws, anti-gradient of concentration determines the occurrence and extent of diffusion in certain molecules. Hubbard, Lund, and Halter (2013) hold that Fick’s laws support Boltzmann’s equation, and thus, they are helpful in predicting the movement of molecules. Therefore, Fick’s laws indicate that diffusion is a physical process that is subject to the concentration gradient and the position of molecules.
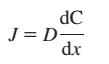
Applications
Osmosis has notable applications in diverse fields such as physics, physical chemistry, pharmacology, medicine, and biophysics. In physics and physical chemistry, reverse osmosis is a process involved in desalination of salt water to obtain fresh water. Since dilution of drugs requires clean water, pharmaceutical industry also uses reverse osmosis in producing purified water and water for injection. Osmosis also applies in medicine as medical providers use isotonic solutions in preserving the integrity of tissues and blood cells. Biophysics effectively illustrates the mechanism in which plants absorb water from the soil and distribute in all cells using the process of osmosis.
Diffusion also has extensive application because it elucidates the movement of molecules, particles, and other forms of matter in a given space or environment. In pharmacology, diffusion is applicable in drug design because it effectively elucidates pharmacodynamics and pharmacokinetics, which define efficacy, safety, and mechanisms of action. Physicists and physical chemists apply physics of diffusion in studying thermodynamics, kinetics, entropy, enthalpy, and pressure. Biophysicists also apply diffusion in assessing physics and physiology of respiration and the integrity of the respiratory system.
Conclusion
Analysis of osmosis and diffusion shows that they play a central role in elucidating physical process involved in the movement of molecules, particles, and other forms of matter in physics, biology, and chemistry amongst other fields of knowledge. A critical analysis shows that osmosis and diffusion are similar physical processes that are subject to physical laws. However, osmosis requires cell membrane and involves solvent molecules only. In biological systems, osmosis involves the movement of water across cell membranes. Diffusion also occurs in biological systems when it entails the exchange of gases in the alveoli.
Critique of the Sources
The research paper used three research articles in describing physics of cell membrane osmosis and diffusion. The first article by Elmoazzen, Elliot, and McGann (2009) describes equations of osmotic transport with a view of elucidating a new equation that applies to non-dilute solutes. The article presents the physics of osmosis correctly because it uses numerous equations. Moreover, the physics of osmosis are understandable since the article clearly shows derivations of 38 equations. Therefore, the use of equations and their derivations depicts physics and promotes understanding of osmosis.
The second article by Hubbard, Lund, and Halter (2013) also correctly presents the physics of diffusion using numerous equations, which effectively illustrate the physical process of diffusion. Specifically, the article focuses on Boltzmann’s function and derives 36 equations, which effectively enhances understanding of diffusion. The third article by Zhou, Nyberg, and Rowat (2015) examines diffusion from the perspective of Fick’s laws. The article correctly presents physics of diffusion using Fick’s law, but the presentation is not understandable because it does not illustrate derivation of diverse relevant equations. Essentially, the article concentrates on explaining the application of the Fick’s law in diffusion using limited equations of physics.
References
Elmoazzen, H., Elliot, J., & McGann, L. (2009). Osmotic transport across cell membranes in nondilute solutes: A new nondilute transport equation. Biophysical Journal, 96(1), 2559-2571.
Hubbard, J., Lund, S., & Halter, M. (2013). Boltzmann’s H-Function and Diffusion Processes. Journal of Physical Chemistry, 117(42), 12836-12843.
Zhou, L., Nyberg, K., & Rowat, A. (2015). Understanding diffusion theory and Fick’s law through food and cooking. Advances in Physiology Education, 39(3), 192-197.