Abstract
Cell membranes are thin semipermeable barriers that separate the internal and external cellular environments. This protects and regulates the intracellular composed of saturated and unsaturated fatty acid chains whose neutral hydrocarbons account for conditions, allows the cell to communicate using an electrical gradient, and can be used for external adhesion. This paper will cover the history of cell membrane theory. Additional focus will examine the ion conductivity properties of the cellular membrane as exemplified by the neuron and as modeled by the Nernst, and Goldman Hogkin Katz equations.
Introduction (Cellular Membranes)
The cellular membrane is composed of a phospholipid bilayer with embedded proteins. The lipids are amphipathic, having a hydrophobic tail and a hydrophilic head. This property makes the lipids spontaneously arrange into a wall which shields the hydrophobic tails inside the wall; meanwhile the hydrophilic heads associate with the intracellular and extracellular fluid.
A group of phosphate that has glycerol bond forms the heads. Oxygen that is negatively charged in the phosphate gives the heads the nature of being hydrophilic. The hydrophobic tail is the hydrophobia. Various bonds form and sustain lipid bilayer. Examples of the bonds include hydrogen and covalent bonds.
The membrane has unique feature of impermeability to polar molecules and ions and allowing permeability to hydrophobic molecules. The movement of ions across the membrane is regulated by proteins that span the phospholipid bilayer in the form of pores, channels, and gates. The fluid nature of the phospholipids and structural qualities of the proteins combine to form the fluid mosaic cell model (Nicolson 1972).
History of Cell Membrane Theory
Before biology, which is derived etymologically from the Greek study of life, the term natural history was used to describe the science of living things. This branch of science was half philosophical in nature, dealing with issues of the origins of life and theology as well as geology, physics, chemistry, and astronomy. Aristotle, a Greek philosopher, formed the foundation of western biology with his theory called the Great Chain of Being which ranked lifeforms on a scale of perfection with humanity on the top. After Aristotle there were numerous theories and natural historians, but the fall of the Roman Empire led western thought into a scientific blackout until the renaissance allowed scientists to begin exploring the initial questions these philosophers speculated.
The Development of Cell Theory
The existence of cells was first observed in 1665 by Robert Hooke who used a compound microscope to observe cork (Clarke). Five years later, the first living cells were observed by Anton van Leeuwenhoek, although these could still only be observed in plants because of their prominent cell wall. Animal cells were thought to have similar structures, but beside for bacteria they would not be discovered until the mid-19th century. That was a century and half after the cells discovery when Robert Brown observed the cells center. Robert, isolated the nucleus found in cells of plants. In 1838, the discovery was enhanced by Mathias Jacob Schleiden. Mathias discovered that the building blocks of plants were cells. That discovery formed the basis of the universal cell theory.
A year later in 1839 Theodor Schwann expanded the theory to include animal life and unified the cell theory. Theodor stated that cells were essential units of living organisms. According to Theodor, a living organism was made of one or more cells. This prompted further research into animal cells, leading to the discovery that sperm and eggs in humans are also cells in 1840. Carl Heinrich Braun is responsible for refining the theory and classifying cells as the basic unit of all life in 1845, and the final element of modern cell theory was added by Rudolf Virchow who stated that all cells are produced from other cells in 1855.
Cell Membrane Theory
Moritz Traube in the mid-19th century was the first to note that the other layer of cells must be permeable to allow the passage of ions and nutrients into the cell (Nicolson). Moritz noted that the interfacial reaction between extracellular fluid and intracellular protoplasm produced cell film. Quincke discovered that lipids were constituents of cell membrane. Quincke noted that cells that were split into half produced two smaller circles. Quincke predicted a membrane made of a material similar to oil because of its similar properties. Ernest Overton and HansMeyer further enhanced the theory membrane. They discovered that anesthetic were chemicals both soluble in oil and water. They developed a lipid theory of narcosis which speculated that the membrane must be lipid-based because the anesthetics must be soluble in oil.
Pfeffer first proposed the membrane theory in 1877. The theory explains single cell membrane’s mechanisms of permeability and impermeability. In 1889, the selective permeability in cells was shown when cells were placed in various solvents and the time that they took to lyse from swelling was recorded. The membrane’s high permeability to water was covered by Nathansohn’s mosaic theory in 1904. This theory hypothesized that the membrane was only partly constructed of lipids, while the rest of it was made up of a semipermeable gel.
Fricke in 1924 used this information to perform experiments designed to discover the structure of this lipid membrane. He was able to measure the membrane width as approximately 3.3 nm by testing capacitance across it, although he interpreted these results to indicate that the membrane was a single layer. The polar lipid heads did not show results on his capacitance test, meaning that he was only receiving data from the hydrophobic center of the membrane. Gorter and Grendel performed an experiment which spread a membrane out as a monolayer, which led them to discover a two to one ratio between their dismantled spread and the surface of cells. This discovery led to the first model of a lipid bilayer. In 1939, the lipid bilayer was officially suggested by Danielli and Harvey. They added that the lipid were covered by a protein layer; hence, surface tension was observable.
The first membrane pump was discovered with the technology of radioactive tracers which showed that cells are permeable to sodium even though the lipid bilayer is not. In order to expand the hypothesis of pump, the membrane theory was refined. The people accredited with refining and further computation of the membranes potential include Hodgkin, Huxley and Katz.
Fluid mosaic is accepted in the current setting. The advancement of the model was by Edidin and Frye. The advancements of the model dates back to 1970. They used florescent tags on two different cells and observed their interaction Two years later, Singer and Nicolson developed the modern fluid mosaic model. The model describes the existence of transmembrane proteins that are embedded within the lipid bilayer. These proteins are mostly unanchored and float freely through the sea of lipids, giving it its fluid nature. Modern research has refined the theory to include the construction of the transmembrane proteins, cytoskeletal protein anchors, and other structural details.
Transmembrane Proteins
Electrical gradients inside the cell are maintained by the proteins embedded within the membrane. They can be divided into four categories:
- Voltage gated channels remain closed until activated by an electrical potential across the membrane. Their main function is to create an action potential after an appropriately large signal has been received.
- Neurotransmitter is signaled to activate channels that chemically gated or the ligand. The channels have the ability to open in order to allow the passage of ions through the membrane after the activation of neurotransmitter.
- Leakage channels are continually open and allow free diffusion of one or more ions as is appropriate to its relative concentration gradients across the cell membrane.
- Mechanically gated ion channels are activated in response to pressure or vibration.
- Light gated ion channels are activated in response to high energy photons.
Passive and active transport
The ions transportation across the membrane is either passively or actively. Active transport requires an input of energy (usually derived from removing the third phosphate group from ATP to form ADP) to move ions against their concentration gradient. This is continually used by the sodium potassium pump which must move the ions against their gradients in order to maintain the negative resting potential in cells. In passive transport ions simply diffuse across the membrane with the aid of leakage channels in the same manner as ions in a solution that does not have a plasma membrane.
Electrochemical Equilibrium
The passive and active transport are influenced by the ion concentration in the sides of membranes. In addition, the concentrations of the electrochemical in the sides of the membranes influence the passive and active transport. Large proteins generally have a negative charge and cannot pass through the ion channels in the membrane. This makes the intracellular charge negative before ion transport is accounted for. The process of diffusion aids the movement of potassium ions from the cell. However, the diffusion is influenced by the concentration of the potassium. The diffusion takes place until the electrical force of the potassium concentration is lesser that of the gradient force.
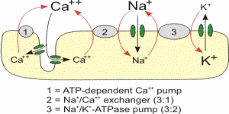
Structure of Neuron
Neuron consist of cells whose sole purpose to receive and transmit electrical signals. These are communicated via an electrical gradient maintained across the membrane which is controlled by the embedded proteins, making it the perfect cell to exemplify the properties of this system. There are three parts of neurons. They comprise the axon, soma and dendrites. The soma is the cell body which houses structures critical for cellular function. The dendrites are a mass of thin receptor branches that span great lengths and receive information from the axon of other neurons, which initiates the signal.
Neurons have an equilibrium charge of -65 mV called the resting potential. This voltage can be manipulated by ion the channels which move sodium, potassium, chloride, and calcium across the membrane. When the voltage change hits a threshold mark, an action potential is exhibited in the cell which is propagated along the axon and communicates with the dendrites of neighboring neurons.
Action Potential
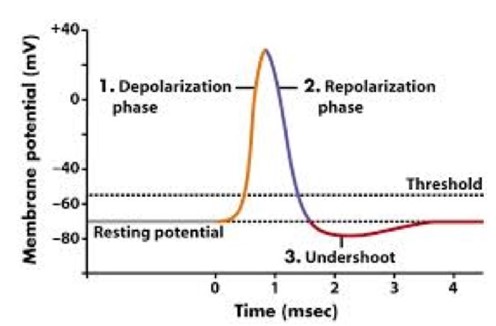
Before the neuron is stimulated, the resting potential voltage is maintained by the sodium and potassium pump in the membrane. Positive sodium ions are constantly transported outside of the cell, while a smaller number of positive potassium ions are exchanged inside of the cell to create the negative resting gradient. When a stimulus is received, the following steps will occur to formulate the action potential (Connors, Figure 2).
The sodium channels in the membrane will open in response to the stimulus. These gated ion channels allow the sodium to rush inside the cell, depolarizing it.
Weak stimuli will not keep the sodium channels open for long. In these cases the sodium potassium pump will return the sodium to the extracellular fluid, and the action potential will not fire.
Strong stimuli will open more channels and keep them open for longer until the electrical gradient has decreased to approximately -55 mV. This threshold causes the sodium channels to close while opening the potassium channels. Potassium ions now move outside while sodium ions remain inside, repolarizing the cell in the opposite direction. The action potential is generated, and the electrical gradient spikes to approximately positive 40 mV.
The cell becomes hyper-polarized, and the electrical gradient has been maximized when there is more potassium outside the cell than within it. This prompts the potassium gates to close. The electrical potential drops to approximately -70 mV, which is below the initial resting potential, and the cell is unable to undergo another action potential during this refractory period.
Propagating the Action Potential
The action potential generated by the axon spread to depolarize neighboring areas of the cell membrane, thus propagating the current through the cell. Voltage gated channels are responsible for determining when part of the membrane is depolarized, which opens potassium channels further along the membrane. The axon parts in which the current passes through display a period of refractory similar to that exhibited after the passage of potential action in the parts. In The result is the prevention of firing of the of the multiple signal in reaction to a similar stimulus. The refractory period is categorized into relative refractory and absolute refractory. The rate at which a signal fires when in relative refractory period is an effective way to communicate the intensity of the stimulus.
The axons of some neurons are wrapped in a myelin sheath which increases the speed that action potentials propagate. The oligodendrocytes and Schwann produce myelin. The location of the oligodendrocytes is in the central nervous system. On the other hand, the peripheral system contain the Schwann. The sheath wraps the axon in segments, with un-myelinated segments between called nodes of Ranvier. Ions cannot permeate the myelin sheath, and action potentials cannot propagate through it. Therefore, through salutatory conduction process, the current moves a Ranvier node to the other, thus the signal velocity is increased.
Synapses
Once the action potential has reached the end of its axon, it synapses with the neighboring dendrites of the neuron it is communicating with. This can either be in the form of a chemical synapse, an electrical synapse, or a neuromuscular junction.
- Chemical Synapse: the action potential triggers the release of neurotransmitter’s from the axon to cross the synapse and communicate with receptors on the dendrite. The neurotransmitter generally triggers gated channels in the receiving cell to open to continue the signal.
- Electrical synapses: The action potential crosses directly to the postsynaptic cell through pores called connexons without a chemical messenger. The production of the ifromation is not specific. However, compared with chemical synapses, faster responses are emitted. 3. Neuromuscular junctions: The final neuron at the end of the synaptic chain will synapse directly with the target cell to deliver the message. The neurotransmitter acetylcholine is released from the axon to terminate on the muscle fiber, prompting it to undergo its own action potential which flexes the muscle.
The Nernst equation
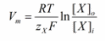
Derivation
In a membrane that has selectively permeable channels, the equilibrium of the electrochemical is determined by application of the Nernst equation. The Nernst potential denotes a membrane that is equilibrium. The two compartments being used will be represented by “i” for inside the cell and “o” for outside of a cell which has channels for ion “X”. The equation describes ideal conditions where the channels are selective only to ion X, and there are no other types of channels present for the counter ion, designated as “Y”.
Inside the cell, the chemical potential is denoted by “μiX”. On the other hand, the chemical potential outside the cell is represented by “μoX” “RTln[X]” accounts for the chemical potential based on the concentration of ion X while “zXFV” accounts for the electrical component. 8.314 J.K-1 is the constant for universal gas representing the variable “R”. mol-1, J/ (mol. K), “T”, the temperature in Kelvin, “zX” which is the valence for ion X, and “F” which is Faraday’s constant (96485 C.mol-1, C/mol).
Intracellular chemical potential: 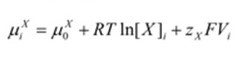
Extracellular chemical potential: 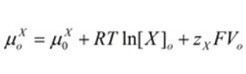
For the equilibrium of electrochemical to be achieved, the “μiX” term must equal the “μoX” term in these equations.
When the terms are set as equal the equations can be combined to form a new equation which represents the total chemical potential:
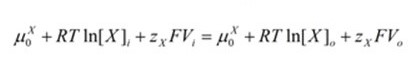
Which can be simplified by combining like terms and the properties of logarithms:
Simplified total chemical potential:
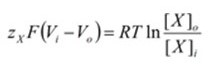
The new term “Vi – Vo” defines the electrical potential difference between the interior and exterior of the cell, also known as the membrane potential, or “Vm”. Replacing the term will change the formula to:
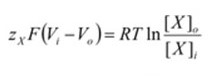
When the Vm term is solved for, the final form of the Nernst equation can be derived.
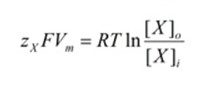
Nernst Equation Discussion
The equilibrium potential of an ion is verified potential by use of the Nernst equation final form. In cellular conditions, this represents the state where there is no movement for ion X across the membrane even when channels for it are open. Because the ion movement is based on electrical and chemical concentrations, when the ion concentrations within and without the cell are equal (Xo = Xi), the equilibrium potential will be calculated to be 0.
When there are more ions than X in the system, the equation will still only predict the equilibrium potential for X, and so it is no longer valid for determining the cellular potential. At the equilibrium, potential, individual ions will not balance. An electrical driving force that is down the electrochemical gradient exists in cases where the ion is not at its potential. The difference between the membrane potential (Vm) and potential of the equilibrium (Veq) is equal to the “VDF”.
The Goldman-Hodgkin-Katz Equation
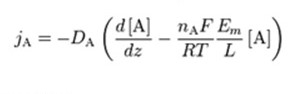
Derivation
The Goldman Hogkin Katz equation (GHK) accounts for conditions where there is more than one ion being considered, and thus more accurately reflects real living conditions (Gierke). Potassium (K+), sodium (Na+), and calcium (Cl-) are the greatest contributors to membrane potential. Normal conditions maintain a negative resting potential of approximately -65mV, (as was previously discussed in section III. A.) The GHK equation can also predict the reversal potential (Vrev).
The measure of the ease of passing through the membrane is achieved by the following permeabilities; pCl, pNa and pK. A higher permeability indicates that there is a greater number of active channels specific to that ion. They are represented in the equation as “DA/L”, which is the diffusion constant over the thickness of the membrane. When the channel is completely closed, the permeability for that ion is considered to be 0. In resting cellular conditions, these values are typically pK : pNa : pCl = 1 : 0.05 : 0.45. During an action potential, these numbers fluctuate greatly: pK : pNa : pCl = 1 : 12 : 0.45.
The term jA is associated with Fick’s law of diffusion, giving the ion flux from diffusion down its concentration gradient. “qA” is the charge of the ion “A”. The direction across the membrane is denoted by “z”. It is the only direction applied in the coordinate system of the Cartesian. This makes “μ” be considered a dimensionless number. The constants are charge valence (nA), temperature in kelvin (T), gas constant (R), and Faraday’s constant (F). in order to derive the equation, the steps followed include:
Separate the variables:
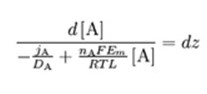
Integrate from z=0 (inside the membrane) to z=L (outside the membrane):
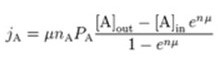
μ can be calculated to equal:
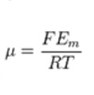
The ionic permeability is:
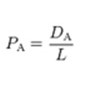
The electric current density is:
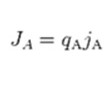
At equilibrium the total current density (jtot) is zero, therefore:
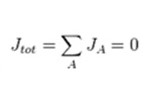
Assuming all ions are monovalent (nA = +/- 1), this can be expressed as:
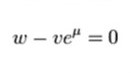
This can then be solved to the final Goldman equation:
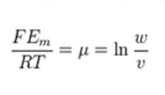
Discussing the Goldman and Nernst Equations
The Goldman equation is much more useful than the Nernst equation in calculating non-idealized cells because of its ability to incorporate multiple ions. The proximity each individual ion gets to its ionic equilibrium is directly dependent on the permeability of that ion, which in turn is dependent on the number of channels. This means that the cell can be at electrochemical equilibrium while individual types of ions are each out of equilibrium, and that those ions with highest permeability are closest to their equilibrium when the cell is at equilibrium. As the Nernst equation only deals with single ions, it also does not account for the relative permeability of multiple ions.
Electrical circuits and Nernst
The calculation of electrical potential across two compartments for an ion that is single is achieved by use of Nernst equation. This does not necessitate a membrane, and is used in electrical engineering as well as biology.
For example, the Nernst equation can be used to represent an electrical circuit of galvanic cell in which the ions are split to make two compartments. In the galvanic cell, an oxidation-reduction reaction takes place between two compartments divided by a salt bridge. The main components include as submerged cathode and electrode of solid metal in cations solutions of the anions and electrodes in order to achieve a balance of the charge. It was the first electric battery, able to store electrical potential energy.
In this example (Figure 3), a galvanic cell using zinc (Zn), chloride (Cl), copper (Cu), and potassium (K) is used. The zinc electrode loses mass as the Zn is oxidized into Zn2+, which dissolves into the solution of one of the compartments. This attracts anion (Cl-) from the other compartment to flow from the salt bridge toward the zinc. The copper electrode gains mass as Cu2+ ions are taken out of solution and the cation K+ will flow from the salt bridge toward the cathode. Moving to the equilibrium, the gradient’s concentration force, determines the battery strength. The Nernst equation can be used to present the gradient’s concentration force.In the case discussed above, the Nernst equation forms the basis of calculation. It is thus used to determine the potential energy of the cell. The calculation entails multiplication of the anode oxidation reaction by cathode reduction reaction. The reactions in the cathode and the anode are calculated by use of Nernst equation. The cell potential is achieved by calculation of the electrons lowest common multiple.
Equivalence Circuit
The equivalence circuit, an idealized circuit used in calculation, is a more sophisticated example of this principle. The Goldman equation can simplify the cellular membrane into to an RC circuit. The capacitance in this circuit can represent the lipid bilayer, and the resistance-DC voltage is analogous to the ion channels in the membrane. The elements in a biological equivalence circuit are the following:
Capacitor
Stores electrostatic energy in an electric field using two electrical conductors separated by a dielectric. In biological systems, this value is dependent on the plasma membrane and is thus static.
Parallel pathways
In the case of parallel pathways, ions from the various chemicals are used to denote the cellular gradient. Examples of the chemicals include the chloride and potassium. The concentration of the ions is determines the pathway voltage. The conductance is dependent on the number of active channels selective to that ion.
Discussion and summary
The history of science is a steady progression of theories, technology, and more sophisticated experiments, which build upon the work of predecessors. Each individual breakthrough is used as groundwork for the next generation of scientists who are able to refine humanity’s understanding of the world. From the natural philosophers in ancient Greece to modern electron microscopes, mankind is in a constant state of overturning its own knowledge and reaching deeper levels of understanding. Current theories about the nature of cells and their membranes are by no means the final answer, and further research and insight will constantly evolve scientific understanding.
The strength of a scientific theory rests on its ability to accurately predict the world around us, and thanks to the equations of Nernst, Goldman, Hodgkin, and Katz, cellular conditions are able to be calculated to a high degree of accuracy. All mathematical representations are a simplified version of reality however, and future equations that take more variables into account will continue to advance our understanding of cellular conditions. The Nernst equations work perfectly in idealized scenarios, but their failure to account for multiple ions makes them highly situational. The Goldman, Hodgkin, and Katz equation accounts for more, but future models which take into account ambient protein charges, cellular fluid pressures, or a myriad of other environmental conditions will continue to refine the formulas.
The applications of this research stretches far beyond biology as electrical engineers use principles of the body to construct ever more elaborate devices. Polymer membrane fuel technology, electric cells, surgical tissue repair, and a myriad of other fields are able to unify and extrapolate the information to their respective fields. In the same respect, medicine progresses as interrelated fields utilize their advancements in artificial organs, electron resonance imagery, patient care, and a thousand different ways. It is the unification of different scientific fields that continues humanity’s unending march of progress.
References
Budin, Itay; Devaraj, Neal K. Membrane Assembly Driven by a Biomimetic Coupling Reaction. Journal of the American Chemical Society, 2011. Print.
Clarke, Edwin. Nineteenth-Century Origins of Neuroscientific Concepts, University of California Press, 1992. Print.
Connors B, Long M. Electrical synapses in the mammalian brain”. Annual Revised Neuroscience, 2004. Print.
Djurisic M, Antic S, Chen W, Zecevic D. Voltage imaging from dendrites of mitral cells: EPSP attenuation and spike trigger zones. J Neuroscience, 24. 2004, Print.
Drachman D. Do we have brain to spare? Neurology 64 (12), 2004. Print.
Dugnes, Sarah. Nernst Equation: Derivation. Physiology Web, 2011.
Faraday, Michael. History of Science and Technology. Houghton Mifflin Company, 2004. Web.
Gierke, Henning,, David E. Goldman, 1910–1998, The Journal of the Acoustical Society of America 106 (3): 1225, 1999. Print.
Johnson, D. Origins of the equivalent circuit concept: the voltage-source equivalent. Proceedings of the IEEE 91 (4), 2003. Web.
Junge D. Nerve and Muscle Excitation (2nd edition ed.) Sunderland, Massachusetts: Sinauer Associates. pp. 33–37, 1981. Print.
Klabunde, Richard. Sodium-Calcium Exchange in Cardiac Cells. Cardiovascular physiology concepts: 2010. Web.
Nicolson, Singer. The fluid mosaic model of the structure of cell membranes. Science Journal, 175 (4023): 1972, Print.
Thorpe, SJ. Spike arrival times: A highly efficient coding scheme for neural networks. New York, NY: Random House. 1990, Print.
Weinstein, Joshua. Electrochemistry : Faraday’s Law & Nernst Equation. Chem, tamu, 2007. Web.