Introduction
Stocks’ beta expresses how much the stock prices may change as a result of changes in the financial market prices. A stock’s beta of 1.06 indicates that for a 1% change in general market prices, the price of the particular stock will change by 1.06%. Such a stock price is considered to be less volatile.
Assets’ beta is the average of the different sources of finance that a firm chooses. The assets’ beta for a company that has been financed without debts is equal to equity’s beta. Weighted cost of capital represents the least amount of return that an investment can offer stakeholders.
When the expected rate of return from a project is lower than WACC, it is considered unviable. Managers may consider those that break-even because of the economic level of returns. However, a project must have a higher rate of return than WACC before wealth is created for holders of securities.
A majority of firms uses debts to finance growth rather than wait for the profits. Fabozzi et al. (2008, p. 507) discuss that when a firm has no debt, “the beta of its equity is the same as its assets’ beta.” They also note that it is very rare for a company to operate without incurring some debts. Using debts makes a company’s equity riskier.
Fabozzi et al. (2008, p. 507) explain that financial leverage causes “the market risk of a company’s stock to be higher than its asset’s risk.” In that case, equity’s beta exceeds assets’ beta. When the firms choose to fund assets by a combination of equity and debts, the risk involved is shared between the two groups of stakeholders.
Fabozzi et al. (2008, p. 508) discuss that the “asset market risk is the weighted average of the company’s debt beta and equity beta because the asset’s risk is shared between creditors and owners.” In simple terms, the asset beta = debts beta (fraction of assets from debts) + equity beta (fraction of assets from equity).
The equation of assets’ beta average is true because the variations from equity’s and stocks’ betas are correlated. The effect on one source of capital influences the chance of the other sources volatility. Corporate taxable income is generated after deductions of interest paid on loans. The effect reduces what a firm pays as tax which makes their burden less. On the other hand, interest received by creditors is taxed after it is paid to them.
As a result of interest on debt being deductible, debts beta in most cases is assumed to be negligible. WACC is used to “evaluate the impact of debt-financing on risk and returns to investments” (Geltner et al. 2010, p. 307). Leverage is a term used to describe the common practice used by firms to fund their projects from debts, and equity. The WACC is derived from the formula of basic holding period return (HPR).
The formula expresses assets as a sum of debts and equities. It also equates property cash flow to the sum of debt cash flow and equity cash flow. The returns received are shared by holders, and creditors. It is derived from the returns to capital generated by the firm.
WACC represents the least rate of return on a project that evaluators consider before allowing a business plan to be implemented. The formula for WACC as presented by Hawawini & Viallet (2011, p. 410) is shown below. In this case, kE represents cost of equity and kD is the cost of debt before taxation.
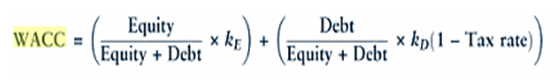
Bierman (p. 195) discusses that WACC can be interpreted as “the cost of both current capital and an additional dollar of new capital if the existing capital structure is maintained”. The existing capital structure refers to the percentage of debt and securities that have been used to finance a project. Debts tend to reduce WACC because of tax deductions.
As it can be seen in the formula “1 – tax rate” has a lesser effect on WACC compared to equity when the cost of capital is considered equal for both equities. WACC includes returns to creditors and shareholders. Baker and Martin discuss that WACC is the “cost of raising funds to the firm” (2011, p. 192). On the other hand, it is the rate of return that investors consider before lending a firm.
Creditors receive interest on money owed to them. Shareholders expect dividends, and gains in market value. The gains in market value are only possible if the firm chooses growth opportunities with higher rates of return than WACC. A firm can only add value to its capital after exceeding the rate of return owed to investors. The investors evaluate the firm’s strategy, opportunities of growth, and risk.
When a business opportunity promises slow growth, investors consider it as a high risk investment. Slow growth reduces a firm’s ability to repay its debts. For this reason, investors may require higher interest rates which may make a project unviable. The rate of return expected by investors also depends on what other financial assets receive as returns.
Firms choose to finance their assets with a mixture of debt, preference shares and common equity. They choose a mixture that optimizes the price of their stock. Besley and Brigham (2009, p. 485) discuss that WACC “represents the minimum return the firm must earn on its investments to maintain its current level of wealth”.
Besley and Brigham (2009) provide the formula below for calculating WACC.

The WACC of most companies represents the average cost of its capital. Lumby and Jones discuss that the WACC of most companies may not be used to rate individual projects because most companies have their investments diversified (2003, p. 427). The WACC in most cases reflects the “average level of systematic risk throughout all its operations” (Lumby and Jones 2003, p. 427).
Companies consider diversification as a means of reducing risk. The volatility of an individual project carried out by a company is unlikely to be represented by WACC because most companies calculate the overall value.
The returns expected from different securities vary. Different capital sources carry different weights. Lumby and Jones (2003, p. 748) explain that “changing a firm’s capital structure changes its WACC”. Debts are an obligation. They are considered before financial assets. Dividends and other benefits are paid to preference shares before common shares.
Importance of WACC
A higher WACC will require that the performance must be higher before generating wealth for stakeholders. Megginson & Smart discuss that firms use WACC to value the amount of effort needed before the firm can actually generate returns for shareholders (2010, p. 420). The firm’s market value declines if its WACC increases as a result of factors that the firm cannot control.
Megginson & Smart discuss that when a firm’s WACC is increased by an event it cannot address “its existing assets and its prospective investment opportunities become less valuable” (2010, p. 420). Such an effect can be expressed through a drop its market value. Such investments may go for a long period without dividends.
Calculating the cost of capital
Cost of capital involves what investors are willing to receive regularly as a result offering finances. Benninga & Czaczkles discuss that the present value of stock can be obtained from the discounted annuity values using anticipated growth in dividend streams (2000, p. 28). They give an example in which the expected growth of dividends is 10%. The following year, the dividend received on each share is $3. The present value of each share (Po) can be expressed as shown below.
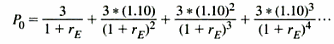
In this case, rE is the cost of equity/discount rate. D1 is used to represent the expected dividend, and g to represent the expected dividend growth rate. According to Benninga & Czaczkes (2000, p. 29), the formula is summarized as shown below.
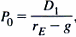
This formula holds only for firms with normal growth. This is the Leonhard Euler derivation. For supernormal growth where g> rE, the Gordon Model is applied.
The formula for the Gordon Model which has been discounted over five years can be expressed as shown below.
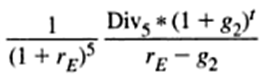
According to Benninga & Czaczkes (2000, p. 31), the cost of equity under Gordon Model is expressed as shown below.
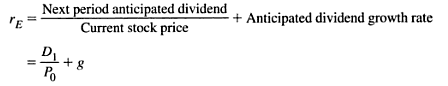
Considering that anticipated dividends can be expressed in terms of the dividends received in the current year (Do). The formula for the cost of equity is expressed as shown below.
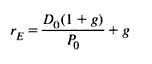
In the classic SML (Security Market Line) model, the formula for calculating the cost of equity is expressed as shown below (Benninga & Czaczkes 2000, p. 35).
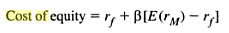
In this case, rf represents the rate at which investment is considered safe, and E(rM) represents the interest rates that the financial market are expected to generate. The risk-free rate of return is reflected in financial assets with the least amount of risk such as interest rates on securities issued by government (Bennninga & Czaczkes 2000). Treasury bills are considered risk-free indicators because governments are unlikely to default. When the expression is adjusted to integrate corporate tax, the expression becomes as shown below (Benninga & Czackles 2000, p. 36).
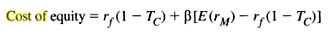
TC is the corporate tax rate.
The cost of newly issued stock is expressed as shown below (Calculating the Cost of Capital n.d., p. 3).
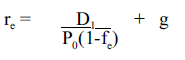
The cost of retained earnings is expressed below using risk-free rate, market expected rate, and stocks beta (Calculating Cost of Capital n.d, p. 2).
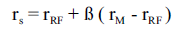
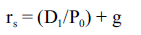
using the discounted cash flow approach.
Cost of debt
The cost of debt has different approaches. Benninga & Czaczkes (2000) discuss that the cost of debt can be estimated using a firm’s existing average cost of debt even though it is not an accurate measure. The cost of debt is expressed as shown below (Calculating Cost of Capital n.d., P. 1).

rd is the rate of return expected by investors to be paid on debts.
Cost of preference capital
Preference capital is associated with preference shares. Debts reduce the amount of corporate tax that a firm is entitled to pay. Khan & Jain (2007) discuss that preference share differs from debts because payments on preference shares are made after tax deductions. Some preference shares are redeemable at maturity while others do not have a fixed maturity date. Both types receive annual fixed rates of return. Khan & Jain (2007, p. 11.10) express the cost of irredeemable shares in two expressions as shown below.
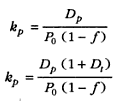
In this case, kp represents cost of preference capital, Dp is the fixed dividend, Po is the expected preference share price, f is the floatation costs expressed as a percentage of share price, and Dt is the tax rate on preference shares dividend.
Preference shares that have a maturity date and a stream of earnings are discounted to a present value. Khan & Jain (2007, p. 11.10) express that the cost of preference shares with a maturity date “is the discount rate that equates the net proceeds of sale of preference shares with the NPV of future dividends and principal repayments”.
This means that capital gains that an individual obtains today from sales are compared to the gains of holding the preference shares to maturity. The cost of preference shares with a maturity date is expressed as shown below.
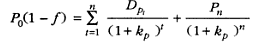
Po represents share price, f is the flotation cost expressed as a percentage of share price, Dp is for dividend, and Pn is the amount paid at maturity. Kumar (2010) gives a more simplified formula for the cost of redeemable share capital as shown below.
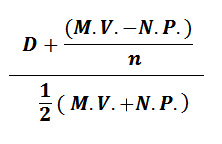
D represents dividends, M.V is the value on maturity, N.P is the net streams gains received on preference shares, n is the number of years.
Using the average cost of 25% tax, the asset beta can be calculated using the formula below. The asset beta is expressed as: asset beta= Equity beta/ (1 + (1 – tax) D/E) (Asset Beta n.d.). D is the percentage of financing received from debts, and E from Equity.
Asset beta = 1.06/ (1+ (1 – 0.25) 0.35/0.65)) = 0.755
However, since the tax rate is still unknown, the cost of equity can be estimated using stocks’ beta and market rate of return. The WACC is then used to express the volatility of expected returns.
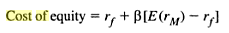
From this formula equity beta can be generated as follows: cost of equity = risk free rate of return + beta (market rate of return – risk free rate)
Cost of equity = 0.0395 + 1.06 (0.0601 – 0.0395) = 0.061336
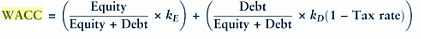
KE is the cost of equity and KD is the cost of debt before taxation
The value of Equity/ total capital can be expressed as:
Equity = 45/60 * 100% = 0.75
The value of debt as a fraction of the total capital is represented as:
Debt = 15/60 * 100% = 0.25
WACC = (0.75 * 0.061336) + (0.25 * 0.0485) = 0.046002 + 0.012125 = 0.058127
This is approximately 0.058. The WACC estimates the least returns expected from investments. It influences the volatility of stock prices.
From the expression in the question:
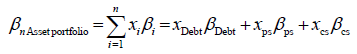
This indicates that the assets’ beta can be calculated from the sum of the product various sources of capital and their beta.
Asset beta = (0.75 * 1.06) + (0.25 * 0.058) = 0.795 + 0.0145 = 0.8095
Asset beta = 0.8095
The volatility of the stock market is derived from the asset beta. A value of less than 1 indicates that the assets are less volatile.
b) The same formula is applied to calculate the asset value of Coral Gambles’ Asset beta by first calculating the WACC. This is used as an estimate of the debt beta. From, the explanations above, the debt beta is always close to zero.
WACC = (0.65 * 0.061336) + (0.35 * 0.0545) = 0.0398684 + 0.019075 = 0.0589434
WACC value of 5.9% (0.0589) indicates that an additional unit of capital may cost the firm 5.9% interest. The firm must invest in projects that generate above the 6% rate of return for shareholders to get capital gains.
Asset beta = (0.65 * 1.06) + (0.35 * 0.059) = 0.689 + 0.02065 = 0.691
According to Bragg (2012, p. 142), the cost of common stock is “risk-free return rate + beta (average stock return – risk free return”. From this formula, it can be derived that stock beta = (cost of stock – risk-free rate) / (expected market return – risk-free rate)
Cost of stock = 0.0395 + 0.691 (0.0601 – 0.0395) = 0.054
Coral Gambles’ Stocks beta = (0.054 – 0.0395) / (0.0601 – 0.0395)
= 0.0145/ 0.0206 = 0.7039
The common stock’s beta indicates the value by which the firm’s stock price changes as a result of variations in the general stock prices. A value of 0.7039 indicates that when the market value changes by 1%, the stock price of Coral Gambles varies by 0.7%. This shows that Coral Gamble stock price is less volatile that the overall market prices.

WACC = (0.65 * 0.0601) + (0.35 * 0.0545 (1 – 0.25)) = 0.039065 + 0.0143 = 0.053365
From this calculation, it can be interpreted that investments must generate above the 5% rate of return for the project to add value to shareholders. The least acceptable cost of capital is 5%. This is the point where the firm operates at break-even.
Conclusion
The market stock’s beta of the similar company is more volatile than Coral Gamble stocks or the general market price. Coral Gamble stock price is less volatile than the average market prices. The WACC for both companies indicate that the CFO needs to search for growth opportunities that generate more than 6% rate of return. Investors may consider interest rates that are close to 5%.
The price (Po) generated in the calculation of share price is the discounted value of the current share price, and expected income streams. The income streams are paid to shareholders as yield per share or dividends. The assets’ beta indicates less volatility than stocks’ beta.
However, the stock’s beta generates its volatility from assets’ beta. The Coral Gamble assets’ beta indicates that the firm’s assets are more stable than shifts in market prices, and interest rates. The asset beta has been calculated as a sum of the impact caused by the volatilities of different sources of capital. It can also be calculated from the equity beta, ratio of debts to equity, and tax rate.
Equity beta is the beta quoted by financial reports as stock price volatility. Assets’ beta is equal to equity in situations where a firm has not used debts to finance its assets. The impact of debts’ beta on asset beta is reduced by the fact that it reduces corporate tax.
Reference List
Asset Beta n.d. Web.
Baker, H, & Martin, G 2011, Capital Structure and Corporate Financing Decisions: Theory, Evidence, and Practice, John Wiley & Sons, Hoboken.
Benninga, S, & Czaczkes, B 2000, Financial Modeling, Massachusetts Institute of Technology, Cambridge.
Besley, S, & Brigham, E 2009, Principles of Finance, South-Western Cengage Learning, Mason.
Bierman, H 2010, An Introduction to Accounting and Mangerial Finance: A Merger of Equals, World Scientific Publishing, London.
Bragg, S 2012, Business Ratios and Formulas: A Comprehensive Guide, John Wiley & Sons, Hoboken.
Calculating the Cost of Capital. n.d. Web.
Fabozzi, J. F, Drake, P. P, & Polimeni, S. R 2008, The Complete CFO Handbook: From Accounting to Accountability, John Wiley & Sons, Hoboken.
Geltner, D, Miller, N, Clayton, J & Eichholtz, P 2010, Commercial Real Estate Analysis & Investments, Cengage Learning, Mason.
Hawawini G, & Viallet, C 2011, Finance for Executives: Managing for Value Creation, South-Western Cengage Learning, Mason.
Khan, M, & Jain, P 2007, Financial management, Tata McGraw-Hill, New Delhi.
Kumar, V 2010, Cost of Preference Share Capital. Web.
Lumby, S, & Jones, C 2003, Corporate Finance: Theory and Practice, South-Western Cengage Learning, Mason.
Megginson, W, & Smart, S 2010, Introduction to Corporate Finance, South-Western Cengage Learning, Mason.