As part of the proposed task, it was necessary to determine the area of any of the shaded shapes of choice, using the formulas for the area of triangles and rectangles. The selected figure is shown in the figure below; it is noteworthy that Pythagoras’ theorem could not be used to solve triangles. As one can see in the Figure below, the shaded figure is a square with another slanted square cut out. The fact that the inner figure is exactly a square is confirmed by the equality of its sides (1 inch each) and the right angles of 90° between the sides.
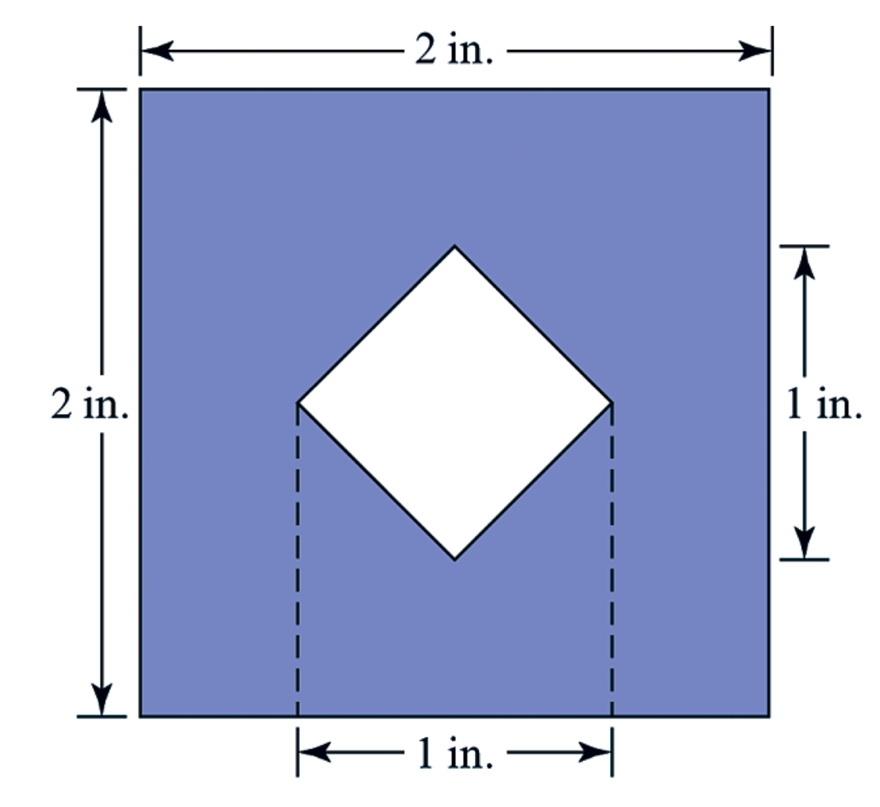
To solve the problem, one can use the subtraction strategy: in this case, the area of the inner square is subtracted from the area of the whole figure. As it is known, the area of a square is calculated as a special case of the area of a rectangle with all sides equal:
If one uses this formula for a large square with two-inch sides, then its area is:
Hence, the area of the shaded figure really should not exceed four square inches. To answer this question, one must determine the area of the small white square in the center of the entire composition. In this case, however, the sides of the square are unknown, but the dimensions of the diagonals are known: they are one inch each. It is worth understanding that the vertical diagonal crosses the horizontal diagonal at exactly half, which means that the height lowered from the top corner of the square to the horizontal diagonal is 0.5 inches. Therefore, the area of the upper triangle can be found by the formula (Pennington, 2022):
But there are two such isosceles triangles as part of the inner square, and they are identical. Then the total area of the small square is determined by the sum of the two interior triangles and is equal to 0.50 square inches. In this case, it is already known that the entire area is equal to 4 square inches, and that the area cut out is equal to 0.50 square inches. Hence elementary, the area of the shaded figure would be 3.50 square inches.
Reference
Pennington, L. (2022). How to find the area of an isosceles triangle. Study. Web.