Inventory Control in the Food Industry Research Paper

Abstract

To formulate a mathematical model to optimize cost in inventory control, it is critical to consider different aspects of inventory control that significantly contribute to the formulation of the model and the reorder policies. Typically, the solution lies in underlying types of inventory systems, the rational for inventories of raw materials used in the food production processes, and the cost of holding stock, that is the raw materials. On the other hand, inventory control constitutes deterministic or stochastic models that bear significantly underlying concepts related to the stock levels enable a firm to identify the critical aspect of specific items used in the food ingredients to make the foods. Thus, the linear programming model with the economic order quantities form a strong complimentary approach to formulating the model and justifying the best order policies, despite some other additional factors influencing the model. Typically, some mathematical models are considered with the inventory level and time factors playing the critical component in addition to the costs incurred in the inventory. Typically, issues worth considering include the reorder cycles, storage costs, procurement costs, and inventory control procedures play a significant role in formulating the ,model. Thus, the model constitutes different aspects and variables.

Introduction

It is important to consider various aspects and parameters that provide the basis for formulating a mathematical model for inventory control in the food industry. These issues include the type of inventory that the model is applied. Typically, there are raw material models where raw materials that are used in the preparation industry are considered, work-in-progress models that factors finished or partially finished products, and finished goods models (Balkhi, 5). However, the current study factors raw materials inventory for the food-processing firm. In that case, therefore, the firm has to consider the aspect of stock costs, which might be due to deliberate policies or replenishment policies, the cost of holding stock that includes storage, deterioration, handling, and interest on capital (Moon, Giri & Ko, 5). On the other hand, the cost of procuring stock also plays a significant role in the cost resulting cost of each of the raw material units, and stockout costs (Robinson, 4). On the other hand, the study considers re-order level systems that are used in inventory control, and periodic review systems that require a review of stock at a constant cycle (Balkhi, 5).

Research Problem

The research problem is to formulate a mathematical model for inventory control in a food-processing firm to obtain the optimum costs, identify the best order policy for its raw materials, and discuss other aspects that might influence the logistics of the company.

Research Questions

1. What are the basic concepts of inventory control?
2. What are the types of models used in inventory control?
3. What are inventory control procedures?
4. How can a linear model be used to minimize costs?

Aim of the Research

The aim of the research is to formulate a mathematical model that can be used to optimize cost in the food-processing firm.

Objectives of the research

1. To identify the concepts related to inventory control
2. To research on the type of models used in inventory control
3. Identify the basic variables used to formulate the mathematical model
4. To formulate the model with the identified variables

Significance of the Research

The current research bears significant benefit to organizational managers particularly in the food industry who face continues problems of uncertainties of what quantities to order in the form of raw materials when processing foods. Typically, foods are easily perishable and have a short lifespan on the shelves. Therefore there is need for the managers and use a specific model that enables them predict, with a high degree of accuracy the quantity of raw materials required to avoid problems associated with inventory control, that include stockout costs. Thus, mangers are also able to minimize the cost of inventories. In addition to that, managers for such firms can build goodwill with the customers, avoid extra costs associated with emergence and unpredictable orders, avoid costs incurred due to production stoppages, avoid loss of future sales, and avoid loss of contributions through lost sales.

Literature Review

Inventory control in the food industry is a basic and important element that management employs to determine stock levels and the movement of stock, beginning from the supply of raw materials for the food industry, to the processing phase, and into the replenishment at the food outlets. Typically, the entire chain extends even to the consumer and covers the recycling phase of the wastes resulting from leftovers. However, the current literature review concentrates on inventory control within the precincts of the food industry and in particular that which is within the management of a company. Therefore, in the context of the current study, the inventory control falls within the supply of raw materials to the inventory of finished products ready for distribution. Of specific importance, therefore, these are the raw materials inventory, the work-in-progress inventory, and the finished products r goods inventory (Lau, 5).

Inventories

Clear views on the types of inventories mentioned above are important to crystallize their meaning. Typically, the raw materials inventory constitutes the components and other materials required to use in the manufacturing processes of the foods. On the other hand, the work-in-progress is a type of inventory that constitutes partially finished products usually occurring between the production phases or processes (Shah, 11). Thus, the work-in-progress phase might not or might be involved in the food industry inventory depending on the type of firm involved in the phases. Typically, that is because other firms might require some finished products as raw materials for the food manufacturing process, while others might be working at the final phases of the industry.

Reasons for Inventory Control

On the other hand, it is important to crystallize the rational for inventory control based on good inventory management policies. Typically, the rationale revolves around the need to satisfy the customers as they are the most critical component in any business organization, and the economic value associated with each of the products in the food chain. In addition to that, the most cost effective transportation policies are another factor worth considering, the level of flexibilities associated with the production processes, and policies of the competing firms since business organizations operate in environments with business rivalries (Axsater, 4).

Other literature in the rationale for inventory control includes ensuring sufficient stocks are made available for any anticipated demand in the food logistics and absorb any changes that might arise in demand, production, and supply (Vrat & Padmanabhan, 22). It also provides a buffer during a work-in-progress when intending to decouple operations, to optimize the benefit associated with bulk purchasing and discounts, meet seasonal fluctuations that might arise due to changes in demand and consumption. In addition to that, inventory control enables smooth and efficient flow in production processes and addresses the effects of inflation (Horowitz, 4). However, the above reasons for inventory control are applicable in a logical situation. Thus, other reasons that might not be logical include the inventory of obsolete items, poor inventory mechanisms, and lack of good coordination between departments. Typically, stock is a critical and deliberate undertaking by a business organization and represents an organization’s investment (Misra, 11). Thus, the cost of holding stock is critical and important and correlates strongly with the benefits of the organization.

Cost of Holding Stock

In the process of formulating a mathematical model for inventory control, it is important to consider a number of factors literature considers essential components in the modeling process. Thus, the carrying or stock holding costs include interests accruing on the capital invested in the stock, cost of storage which include lighting, heating, refrigeration, and air conditioning among other factors. In addition to that, the cost of maintaining equipment and stores staffing significantly contribute to the inventory costs (Mirzazadeh, 8). On the other hand, perpetual inventory costs, auditing costs, and stocktaking costs contribute to the inventory costs as well. Other factors include security, insurance, vermin damage, and deterioration of the food products. Typically, that is because most foods have a short or limited lifespan. On the other hand, the warehousing strategy is another determinant for the overall inventory costs (Maiti, Maiti & Maiti, 20).

Costs of Procuring Stock

The cost of holding stock is complimentary with the cost of procuring stock specifically as it related to the procurement of raw materials. Typically, these costs include clerical and administrative costs, cots of transporting stock, cost of accounting and goods received in the departments, and the set up costs. In addition to that, additional costs include stockout costs (Mirzazadeh, 11). These are associated with the cost incurred due to the contributions incurred due to lost time, future sales lost costs, loss of customer goodwill, costs due to loss of production labor, additional costs incurred due to the need to make urgent orders, which are often in small quantities, and loss of the good will of the customers (Topkis, 3). Thus, research shows that the latter are factors to consider when formulating a mathematical model that provides economic quantities. On the other hand, for the mathematical model to provide a strong and economically feasible control system, it is important to consider available literature on the type of quantitative models used in the inventory control. Typically, research shows that two approaches have been used with significant contributions to efficient and effective inventory controls (Chen, 5). These include deterministic and stochastic models (Mirzazadeh, 10).

Deterministic and Stochastic Models

Deterministic and stochastic models provide inventory control quantitative methods based on the environment inventory controls occur. These environments include a probabilistic environment where the level of certainty is low, while in another environment, the level of certainty is assumed with complete certainty (Yang, 22). Thus, in a stochastic model, the level of certainty is high and of complete certainty. In addition to that, the deterministic model assumes that all factors of production such as demand, usage, carrying costs, and lead-time are well known and hardly an element of uncertainty exists (Chao, 8). On the other hand, the stochastic model is characterized by unknown and undeterminable factors that influence the inventory control of the food production processes (Wee & Law, 21). Examples include a situation with unspecified lead-time and other related factors not known with certainty. It is therefore important when formulating the mathematical model to consider literature on the types of inventory control systems available, and the principles of the inventory control systems. In the context of the current research, in relation to the food industry, it is critical to consider and narrow down to re-order level systems (Yang, Teng & Chern, 22).

The re-order level system is characterized by re-order levels that are characterized by predetermined quantities for each of the items used in the production process of the foods. Typically, there are different items in the form of raw materials used in the manufacturing process. In addition to that, the movement of stock is the predetermining factor on the need to make a re-order of the new stock. Thus, the level of stock movement is correlated strongly to the balance of stock in store. In addition to that, the reorder level introduces the concept of economic order quantities. That is also in view of the fact that costs are incurred when maintaining in in a warehouse (Buzacott, 6). Typically, it is important to note that some of the raw materials required in the food production processes have short lifespans are easily perishable. The Re-Order level system is best illustrated in the following mathematical model. Suppose data about a certain raw material is as in table 1 below.

Table 1

Thus, the Re-Order level can be calculated based on the following mathematical relation.

Re-Order level= Usage at Maximum × Lead Time at Maximum Usage.

• =140 × 30
• =4200 Items

Minimum level = Re-Order level- Average Item usage at Average Lead Time

• =4200-(110 × 27.5)
• =1,175 Items

Maximum level Lead time= Re-Order level +EOQ – Anticipated usage at the minimum

• = 4200+5,000- (50 × 25)
• = 7,950 Items

It is however important to note that once the items have been ordered, it is critical to minimize the costs

Mathematical Models

Research studies on inventory control show that inventory control is based on inflow and outflow of items. Thus, mathematically, inventory movements can be modeled as shown below.

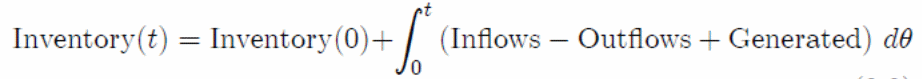
The above model is based on a number of assumptions. These include constant supply of raw materials without any short-term shortages.

The above model draws from inflow and outflow of items shown in the following diagram.

In the above model, t is the time equal to zero. Typically, the above model draws on the formulation of parameters that are specific to the inventory control. That includes environmental factors, manipulating factors, and outputs variables as show in the following block diagram.

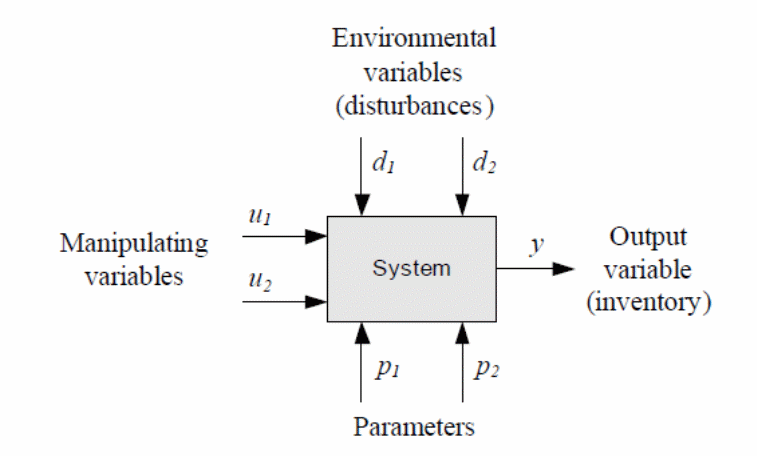
In the above model, the author considers environmental factors to relate to issues such as the probability of an event occurring. These includes issues associated with stochastic models where the variables are either non-determinable. On the other hand, other factors include the certainty of the level of stock movements based on usage and other factors identified above. However, the above model falls short of identifying the point at which cost optimization occurs and provides a general view of a mathematical model that does not widely consider additional issues related to inventory control (Whitin, 12).

On the other hand, certain models consider the reorder cycle with variables based on the demand rates, which are considered well known and understood, which are also considered to vary with time, depend on available stock, and depend on the price of the raw materials (Kawashima, 3).

Another literature on mathematical models that factor stochastic environment includes one that considers the following assumptions. Thus, unsatisfied demand is backlogged according to the above model. On the other hand, the above model revolves around the backorders that are a differential of a decreasing waiting time denoted as t. in addition to that, the ordering considers inflation as an additional factor. However, it is demonstrated clearly that inventory costs increase with increasing time on a stochastic model. On the other hand, it is assumed that items only deteriorate when in stock, thus, replenishment follows an infinite rate with the production levels higher compared with the consumption rate and item deterioration rates. Typically, the model factors inflation rates, discount rates, discount net of inflation, the demand rate, backlogging, and rate of annual productions, deterioration rates, ordering costs, unit costs, and the horizontal time (Wu, Chiang & Chang, 3).

One approach used by Mirzazadeh (42) to formulate a mathematical model includes a number of cycles designated as n with a horizontal time H. Typically, the length of time for the horizontal period is split into T, where T=H/n. Thus, the inventory levels are considered equivalent to zero at this point. Mirzazadeh (42) asserts that it is possible to divide the inventory levels into four distinct groups as discussed on the concepts of inventory control above (Yang, Teng & Chern, 2). It is therefore assumed in the invent control level that production begins at time 0. On the other hand, according to the model, inventory stops at time µ1, with the inventory deteriorating until kT, when shortage is experienced (Sarker & Pan, 33) Thus, the shortage is linear. On the other hand, production begins at time µ2 with a linear decrease until time component T is reached. At that time, inflationary measures take effect at time n1Tstopping at time (n-1) T + µ5. At that point, Mirzazadeh (42) shows that inventory level decreases to the end of the horizontal time as illustrated in fig 1 below.

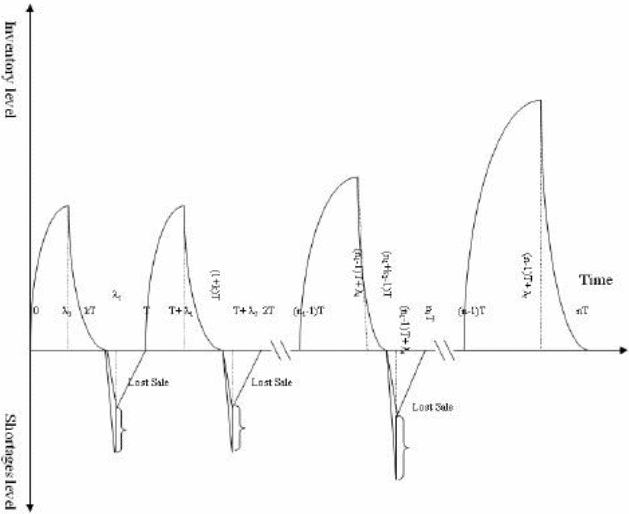
Thus, the equations and inventory are defined by the following differential equations.

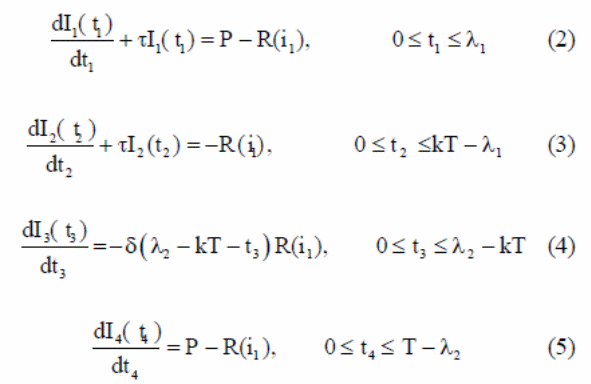
Thus, the above differential equations consider the first inflationary period. On the other hand, the above differential equations can be used to calculate inventory levels. Thus, the above equations can be solved based on the following mathematical equations.

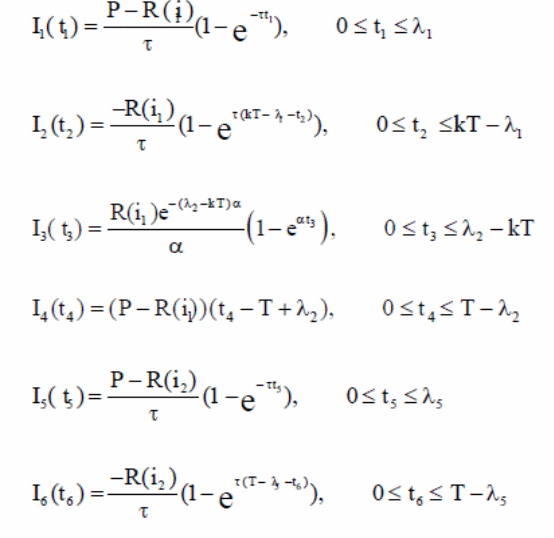
On the other hand, the above relations provide a general method for calculating as follows.

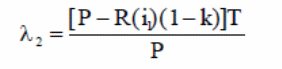
Thus, different models factor different environments for calculating inventory level that are economically viable. Typically, that depends on the environments, some environments allow for stockout while other environments do not allow for stock outs.

The process of formulating am mathematical model also borrows form the concept of inventory control that needs not be a complex task, but a clearly and well-organized process (Robinson, 3). Typically, therefore, that includes inventory planning, order cycles, balancing inventory levels, reviewing of stock levels, and making follow-ups in the inventory control (Moinzadeh & Schmidt, 11)

Inventory Control Procedures

It is a critical requirement that literature on the procedure for carrying out inventory control be studied to provide the basis parameters to consider when formulating the model. Thus, as mentioned above, that includes inventory planning, order cycles, balancing inventory levels, reviewing of stock levels, and making follow-ups in the inventory control systems. Thus, any potential problem associated with inventory control affecting organizations in the food industry can be managed.

It is important as a first step to conduct inventory planning as a prerequisite step in inventory control. In addition to that, inventory planning covers issues associated with the movement of items or raw materials that are used in the food production processes. Thus, typical considerations should also focus on economic order quantities based on environmental and model factors. In addition to that, the amount in units of the raw material should also be considered in the mathematical model (Hou & Lin, 3).

Another step that is if critical importance is establishing the order cycles for the food industry. Order cycles are at times stochastically established and demand and consumption are not always constant factors. Thus, the level of demand, that is, demand might be regular or irregular, it is important to take time and develop a model that specifically meets the specific of the industry in question. In this case, the industry under consideration is the food industry, which faces constant and regular demand for its products (Hou & Lin, 4).

On the other hand, it is important for the food industry to keep itself constantly supplied with raw materials to avoid sense where food runs out of stock in the middle of any season. In addition to that, it is important to factor suppliers when formulating a model, since suppliers of raw materials often face certainty or uncertainty situations (Hou, 7).

It is also important to balance the inventory levels to ensure the firm stays abreast in the market while making good profits with minimal expenditure. Typically, the inventory has to reflect market conditions, reflect current and actual raw material and product turnovers, and remain compatible with the firm’s strategies.

Another component worth integrating into the model is the issue of obsolete inventory. Thus, inventory should be kept up to data and the system should avoid obsolete stock. The following mathematical expression provides the basis upon which a good inventory system works.

In the above case, stock turn is the average rate of items sold annually, and provides the basis for determining predictable levels of stock turnover. On the other hand, carefully measured quantities of stock provide a clear base for determining safe orders. On the other hand, formulating a mathematical model becomes complete when the study considers the concept of economic order quantities (EOQ). Typically, the EOQ minimizes the cost associated with the balance between inventory holding costs and the cost of making new orders.

Economic Order Quantity

Thus, economic order quantity is based on the assumptions that the stock is always constant, known, and the cost of holding stock is also known. In addition to that, the ordering costs is constant and known, the level and rate of demand for the raw materials are known beforehand, and the unit prices of the raw material is known and fixed. On the other hand, the concept works well when the replenishment is done at once without any stocks allowed.

Thus:

• Total costs p.a =ordering costs p.a + carrying costs p.a.
• On the other hand, the ordering cost is calculated as follows.
• Ordering costs p.a = ordering costs p.a × Carrying costs p.a
• On the other hand, the number of orders is calculated as follows.
• No. of orders= Annual Demand/Order Quantity
• On the other hand, carrying costs are obtained as follows.
• Carrying costs p.a= Average stock level × Unit price
• Average stock= order quantity/2

In order to provide a practical application of the concept, the following case study will provide the baseline to comprehend the concept of EOQ.

A food company uses 50,000 items each year costing 10$ each, to buy. After the purchase, the company incurs ordering and handling costs of 150 $ per an order while the carrying costs are 15% of the purchase price per annum. Typically, it costs 1.5 $ to carry each item. Then, the company can use the following mathematical formula to calculate the EOQ for the items or raw materials.

EOQ= ((2*Co.D)/Cc))^1/2

Where Co is the ordering cost per an order, D is the demand of the raw material per annum, and Cc is the carrying cost for each item per annum. Based on the findings, therefore, the EOQ can be calculated as follows.

EOQ = ((2×150×50,000)/1.5)) ^1/2

=3162 items

This method provides accurate figures, considers the level of demand and carrying costs for a similar period, and uses a year as the best period applicable in the model.

On the other hand, when the policy of gradual replenishment is considered, then some adjustments have to be made. Then, the mathematical model is changed as follows.

EOQ= ((2*Co.D)/Cc(1-D/R))^1/2

In the above case, R is the production rate, assuming the production is within the firm under consideration.

Thus, the results based on the above calculation provide the following variation from the other answer.

EOQ = ((2×150×50,000)/1.5((1-(50,000/250,000))) ^½

=3,535 items

One notes that the above value is greater than the previous value. That is because usage occurred during the replenishment period, thus reducing the average stock holding costs.

The Linear Programming Model

Another typical case study example borrows from the liner-programming model to evaluate the best alternative to optimize cost for the inventory control. However, it might be optional to include the model in the model proposed to solve the inventory control. However, the liner-programming model provides one of the best methods for the minimization problem. Typically, minimization is concerned with approaches used to reduce and minimize the costs incurred in executing a task. In the context of the current study, it minimizes costs incurred in inventory control. Thus, it also becomes important in determining minimal costs at some given constraints.

A typical example is a case study of a food-processing firm that requires to a mixture of three basic items, A, B, C to make a certain food. Suppose in the inventory, items in demand and that require replenishment include 100 of item K that requires at least 20 kg of K per day. On the other hand, suppose the firm wants to minimize the inventory cost of item K while ensuring that sufficient amounts of product K are in available. Thus, the following mathematical linear programming model addresses the concerns of the management.

The following statements illustrate the linear programming mathematical model.

Thus, from the above model, it is clear that x1≥0 and X2≥0.

Thus the formula, Minimize 5X1 + 10X2 + 20 X3, fits perfectly well into the model.

Thus, the linear programming model provides a strong basis for considering the issues in formulating an order policy that addresses issues related to the usage and mixing of the ingredients to produce specific foods. That is also because different foods require different ingredient to produce. Thus, the model must factor resources used and resources available as a constraint. On the other hand, ordering raw materials to optimize all costs associated with the raw materials requires that costs be minimized to address the element optimal costs. Thus, the minimization should be sufficient to fulfill the main purpose of producing the food. Thus, a link between the minimization problem and the economic order quantity are complementary.

Methodology

The current study is to formulate a mathematical model of the food industry’s inventory control system to optimize cost. Thus, the research is based on a literature on the concepts related to inventory control, identification the rationale for inventory control, and establish a planned approach for formulating the model. Thus, the current study relies on desk-based literature review and specific procedures for formulating mathematical models that address the above research problem. Typically, the research therefore considers literature on economic order quantities for a firm’s raw materials used in the production of foods in the food industry, and safety stocks, the rationale for safety stocks, and conditions under which raw materials require reordering. In addition to that, the current study considers a mention of other critical factors such as transportation that focused on formulating the firm’s order policy for its raw materials.

Thus, the methodology for the mathematical modeling will borrow from the concept of defining system boundaries for the model, establishing assumptions based on the functionality of the model, and establishing other conditions necessary to formulate the model. In addition to that, the methodology will consider other factors such as inflows into the system under consideration, generated inventory, and outflows. Any inventory system must constitute inputs, inventory, and outputs to create space for more and new inputs and the cycle continues. It is also important to note that the current study is qualitative in nature. On the other hand, it is important to consider the question of economic order quantities as detail din the literature review to obtain the best approach to use to order raw materials economically.

It is important to consider the critical component of the methodology as reflecting on available mathematical models targeting the food industry. In addition to that, the method of research will involve considering the optimization problem by considering a linear programming model that minimizes the inventory costs in the food industry as a minimization problem with parametric limitations. On the other hand, it is important to draw from case study examples to inform the research.

Formulating the Mathematical Model

From the above literature review, it is critical to consider different factors realized during the literature search. Thus, to formulate the model, a number of factors have to be considered. These include annual demand of the raw materials by the firm under consideration, order quantities that are in demand in the firm under consideration, the cost of ordering the raw materials, the carrying costs of the raw materials, the current stock level, and time. Typically, time will lie on the horizontal axis while the current stock level will lie on the vertical axis. It is important to consider the fact that not all the items mentioned above may fit into a single model. That is because different circumstances favor different models. Thus, in the proposed model, some of the factors to consider include integrating the concept of variables such as time, stock levels, and other necessary factors.

Typically, the, model considers the order quantity that the food makes to make appropriate ingredients for the food items to be processed, the cost of ordering the raw materials that are used in the production process, and the carrying costs for each of the raw items. Thus, let the items be specified as follows:

• A=Annual demand for the raw materials
• O =Order quantity
• S= cost of making the order
• C= Carrying cost per an item of quantity O

Suppose the stock at the time of ordering is equivalent to K. On the other hand, a simpler assumption is that, at the ordering time, the average stock is half of the original stock. That implies that:

Average stock= K/2.

Therefore, the cost of holding the annual stock is K × C, while the total number of orders the firm makes in a year are A/ K. therefore, the annual ordering costs are AS/K.

Combining the above equations provides the following mathematical model:

Total cost = KS/2 + (A/K) S

On the other hand, it is important to factor time, which lies on the horizontal axis with respect to inventory. Thus, the order quantity makes the total cost for ordering the items, a differential of the total cost, t_c, at a minimum. Thus,

d t_c/dK=C/2-AS/K²

Considering a situation where the cost is at its minimum, then,

d t_c/dK=0

On the other hand, at minimum cost,

C/2-AS/K²=0.

Thus, the inventory level K, can be obtained from the relations, where K² = 2AS/C

Thus, K= (2AS/C) ^1/2

Thus, the above model is the basic model that can be used generally to factor other variables introduces in the inventory control process. These factors include inventory with gradual replenishment and where stockout is allowed. Thus, the above model is subject to modifications to fit into different inventory environments. Consider a situation where stocks face gradual replenishment. Typically, the profile of a replenish able stock level is shown in graph 1 below.

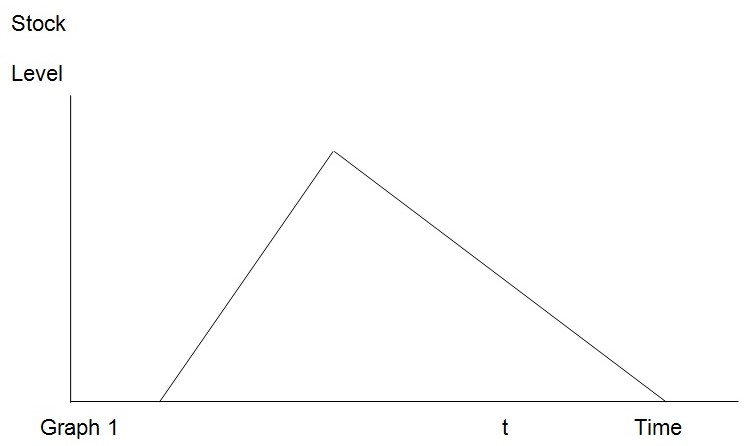
From graph 1 above, time can be calculated based on the following relation. Typically, the rate of replenishment is r occurring over time t. Thus, from the above graph, the average stock is represented by the height of the triangle, which is obtained from the rate of replenishment minus the rate of demand. Thus, demand in this case is a critical component. Therefore, t= K/r.

On the other hand:

• Average stock = t (r-K)/2. When we substitute for t in the equation, then: Average stock = (S/r(r-A))/2
• Therefore, the cost of holding the total annual stock = (S (1-A/r) c))/2

For optimal costs, it is important to create an objective function that allows the firm to identify the most appropriate stock levels. Thus, there is the minimization problem to solve. Typically, in the supply chain of raw materials, the basic limitations to consider are the ingredients and the cost of each of the ingredients. Thus, taking an hypothetical situation of a firm that has with the above inventory, it is critical to express the model mathematically. Suppose the firm produces two food items A and B. suppose A makes a contribution of 3 $ per a food item and B makes 4 $ per a food item. Suppose, also, the firm wishes to establish a daily production plan to maximize the contribution, and that 400 kg of materials of ingredients are available to make the food. In addition to that, suppose 200 food items of A are sold while 100 food items of B are sold in the same period. Then, the problem can be expressed mathematically, to maximize the contributions.

Thus, the model becomes:

Maximize 3A + 4B

In this case, the constraints lead to:

4A + 2B ≤ 1000

4A + 6B ≤1800

A + B ≤400

A ≤40

B ≥10

A≥0

In the above case, A is the number of items of food A and B are items of food B. the constraints are illustrated in the model.

The ingredients constraint for B is 4A + 6B ≤1800 and the constraint for A is 4A + 2B ≤ 1000. Thus, the models can be used calculate the inventory levels for optimal costs, in conjunction with the first model.

Discussions

Order Policy for the Raw Materials

From the above model, and specific application to the food industry, it is important to consider a raw materials order policy that suits the above conditions. Typically, the most appropriate inventory policy is the gradual replenishment policy. The rationale behind this option is demonstrated in the case that preparing foods requires different ingredients and the usage of each ingredient varies. That is to imply that some materials are consumed faster than others, thus, if similar order quantities are made, there is a significant likelihood that loss due to some materials going bad resulting in significant financial losses being experienced.

Factors Affecting Logistics Costs

Combinations of factors help in determining the order policy for the raw materials. These include the buffer stock, which are affected by variations of demand and lead time, and the conditions of certainty and uncertainties. In the case of conditions of certainty, the product between the lead-time and the rate of demand provides the amount of stock to order without the need for buffering the raw materials. That also factors the issue of the length of the lead-time and the rate of demand as holding non-significant impact in influencing the inventory levels.

Other factors include the contributions made by each unit of the raw materials in making the food products. These include contributions per unit of any given item to enable for minimizing the cost incurred in making any mixture, and other redundant constraints that might be required to make the mixtures.

Conclusion and Recommendations

Formulating a mathematical model for the food industry inventory critically borrows from a number of inventory control concepts that play critical roles in the formulation process. However, the critical factors to consider include a number of items such as cost of holding stock, types of inventories and conditions of certainty and uncertainty. In addition to that, the model considers the rate of replenishment, and the time factor in relation to the inventory level. On the other hand, it is important to consider the linear problem associated with minimization problem that enables the producer to select the most appropriate inventory policy based on the ration of the ingredients to use in the production process. However, recommendations have it that it is important to factor sales limitations, the essential characteristics of problems to solve based on different mathematical models in relation to the inventory problem, and the number of constraints and limitations that might exist for the model in the real life environment.

Works Cited

Axsater, Sven. “Continuous review policies for multi-level inventory systems with stochastic demand”. Logistics of Production and Inventory, volume 4 of Handbooks in Operations Research & Management Science. Elsevier, Amsterdam. 1993.

Balkhi, Zaid, T. On the Optimality of Inventory Models with Deteriorating Items for Demand and On-Hand Inventory Dependent Production Rate. IMA Journal Management Mathematics 15 (2004): 67-86

Balkhi, Zaid, T. An optimal solution of a general lot size inventory model with Deteriorated and imperfect products, taking into account inflation and time value of money. International Journal of Systems Science 35 (2004):87-96

Buzacott, John, A. Economic order quantities with inflation. Operational Research Quarterly 26 (1975): 553-558.

Chao, Chang.T. An EOQ model with deteriorating items under inflation when supplier credits linked to order quantity. International Journal of Production Economics 88 (2004): 307-316.

Chen, Jen-Ming. An inventory model for deteriorating items with time-proportional demand and shortages under inflation and time discounting. International Journal of Production Economics 55 (1998): 21-30

Horowitz, Ira. EOQ and inflation uncertainty. International Journal of Production Economics 65 (2000): 217-224.

Hou, Kuo-Lung. & Lin, Li-Chiao. An EOQ model for deteriorating items with price-and stock-dependent selling rates under inflation and time value of money. International Journal of Systems Science 37 (20-6): 1131-1139

Hou, Kuo-Lung. & Lin, Li-Chiao. Optimal Inventory Model with Stock-Dependent Selling Rate under Maximal Total Present Value of Profits. Fourth IASTED International Conference on Modeling, Simulation and Optimization 2004: 7-12.

Hou, Kuo-Lung. An inventory model for deteriorating items with stock-dependent consumption rate and shortages under inflation and time discounting. European Journal of Operational Research 168 (2006): 463-474.

Kawashima, Konosuke. Queueing analysis for input regulation method employing periodic monitoring and control. European Journal of Operational Research Volume 23, 1 (1986):100-107

Lau, Hon-Shiang. Some Extensions Of Ismail-Louderback’s Stochastic Cvp Model Under Optimizing and Satisficing Criteria. Journal of Decision Science Institute. 2007.

Maiti, Ami, K., Maiti, Manas, K. & Maiti, Manoranjan. Two storage inventory model with random planning horizon. Applied Mathematics and Computation 183 (2006): 1084-1097.

Misra, Ram, B. A note on optimal inventory management under inflation. Naval Research Logistics Quarterly 26 (1979): 161-165.

Mirzazadeh, Abolfazl. A Partial Backlogging Mathematical Model under Variable Inflation and Demand with Considering Deterioration Cost. World Applied Sciences Journal 7 (2009): 39-49.

Mirzazadeh, Abolfazl. Effects of uncertain inflationary conditions on inventory models using the average annual cost and the discounted cost. Eighth International Conference on Operations and Quantitative Management (ICOQM-8), Bangkok, (2007):17-20

Mirzazadeh, Abolfazl. Economic order interval under variable inflationary conditions. Hamburg International Conference of Logistics. Hamburg, Germany. 2008.

Moinzadeh, Kamran. & Schmidt, Charles, P. “An (S-1, S) Inventory System With Emergency Orders”. Operations Research 39 (1991): 308–321.

Moon, Ilkyeong, Giri, Bibhas Chandra& Ko, Byungsung. Economic order quantity models for ameliorating/ deteriorating items under inflation and time discounting. European Journal of Operational Research 162 (2005): 773-785

Robinson, Lawrence, W. Optimal and approximate control policies for airline booking with sequential nonmonotonic fare classes in Operations Research 43 (2007): 252-263

Sarker, Bhaba.R. & Pan, Haixu. Effects of inflation and the time value of money on order quantity and allowable shortage. International Journal of Production Economics 34 (1994): 65-72

Shah, Nigam, H. Inventory model for deteriorating items and time value of money for a finite time horizon under the permissible delay in payments. International Journal of Systems Science 37 (2006): 9-15.

Topkis, Donald. M. Optimal Ordering and Rationing Policies in A Non-stationary Dynamic Inventory Model with n Demand Classes[J], Management Science, 1968, 15: 160-176.

Vrat, Prem & Padmanabhan, Govindarajan. An inventory model under inflation for stock-Dependent consumption rate items. Engineering Costs and Production Economics 19 (1990): 379-383.

Wee, Hui, Ming, M. & Law, Sh-Tyan. Economic production lot size for deteriorating items taking account of the time-value of money. Computers and Operations Research 26 (1999): 545-558.

Whitin, Thomson, M. Inventory control and price theory [J]. Management Science 2 (1995): 61-68

Wu, Andy, Chiang, David & Chang, Cheng-Wen. Using Order Admission Control To Maximize Revenue Under Capacity Utilization Requirements In Mto B2b Industries. Journal of the Operations Research Society of Japan. 53 (2010): 4. 270–288

Yang, Hui-Ling, Teng, Jinn-Tsair. & Chern, Maw-Sheng Deterministic inventory lot-size models under inflation with shortages and deterioration for fluctuating demand. Naval Research Logistics 48 (2001): 144-158.

Yang, Hui-Ling, Teng, Jinn-Tsair. & Chern, Maw-Sheng. An inventory model under inflation for deteriorating items with stock-dependent consumption rate and partial backlogging shortages. International Journal of Production Economics.2009.

Yang, Hui-Ling. Two-warehouse partial backlogging inventory models for deteriorating items under inflation. International Journal of Production Economics, 103 (2006): 362-370