Introduction
The great scientific advances witnessed today are based on the contributions made over the centuries by scientists from various parts. One region that has made an enormous contribution to scientific thinking and practice is the Arab world. The greatest contribution to science by this region occurred between the 8th and 13th centuries CE. During this period in history, commonly referred to as the “Islamic Golden Age,” Muslim scientists made significant contributions to the scientific field. One of the scientists who made a remarkable contribution to science through his work in Mathematics and Astronomy was Muhammad ibn Musa al-Khwarizmi (780-850CE). This paper will provide a detailed and simplified historical report on the accomplishments of Al-Khwarizmi.
Brief Background
Abu Abdalla Muhammad Ibn Musa Al-Khwarizmi, simply referred to as “Al-Khwarizmi,” was born in the year 780CE at the town of Khwarizmi in the Persian Empire. His family moved from Persia to a location in South Baghdad while he was a child. Little is known about Al-Khwarizmi’s childhood. While in Baghdad, he was called upon to work as the court astronomer for Caliph Al-Mamun. As the librarian to Al-Mamun, Al-Khwarizmi had the privilege to become a member of the Da’rul Hikma. The Dar-el-Hikma (which translates to House of Wisdom) was an academic institute established by the Fatimid caliphs in Baghdad to advance science in philosophy in the Arab world.
This institution contained knowledge obtained from all over the world, and scholars and scientists visited it to make their contribution to world knowledge or learn from its vast repository. Gaining access to this institute provided Al-Khwarizmi with useful information that helped him in his research into mathematics and astrology. Sayili documents that Al-Khwarizmi’s most prolific years were between 813 and 833 CE, and for some of these years, he was engaged in the House of Wisdom (23). Although a native Persian speaker, Al-Khwarizmi was fluent in Arabic (the language used to communicate Scientific thoughts at the time), making it possible for him to access the numerous academic resources written in Arabic and publish his work to a large audience in the same language.
Al-Khwarizmi’s Contributions
Mathematics
One area where Al-Khwarizmi’s work had tremendous implications was in the mathematical concept of algebra. He engaged in years of research on the subject and, as a result, was able to formulate new knowledge. Al-Khwarizmi was the first mathematician to provide a systematic form of tackling algebraic problems. Hazmy et al. document that he was able to give analytical solutions of linear and quadratic equations, making him the legitimate founder of the concept of Algebra (10). Through his influential work, “Hisab Al-jabr wAl-muqabala,” Al-Khwarizmi was able to decisively differentiate Algebra from other concepts of mathematics such as geometry.
Before his contribution, Algebra was not a unique branch of mathematics since geometry was used to solve problems of an algebraic nature. Shafiq and Al-Roubaie document that Al-Khwarizmi was able to record his original research in published work that constituted his treatises on algebra (165). Al-Khwarizmi’s algebraic concepts were not only theoretical in nature but could be used for practical application. Syed notes that Al-Khwarizmi intended for his work to be used for solving everyday problems (par. 5). His book was intended to provide people with mathematical skills that could be used for activities such as dividing inheritances, measuring lands, and in trade.
Al-Khwarizmi was one of the first scholars to identify the significance of the Hindu number system to mathematics. His influential work, which described these symbols, led to the wide usage of the ten-digit system in the Arab world. Since the Arabs were the first to adopt and fully use this 10 digit system, the system is today called the Arabic number system. Syed confirms that Al-Khwarizmi was among the first mathematicians to “use zero as a place holder in positional base” (par. 30). The future adoption of zero presented significant progress in arithmetic algorithms. It enabled mathematicians to solve previously lengthy mathematical problems in short, efficient ways.
Al-Khwarizmi’s work increased the existing knowledge in trigonometry. By engaging in extensive research into Indian mathematics, Al-Khwarizmi was able to borrow some mathematical concepts from the Indians. He incorporated the Indian sine function into Islamic trigonometry leading to a great advancement in Islamic trigonometry (Berggren 13). Before incorporating the sine function, Muslim mathematicians had based their trigonometric functions in terms of absolute lengths instead of ratios. This method was not efficient, and it could not be used to carry out complicated computations. By introducing the sine function, Al-Khwarizmi enabled mathematicians to refine the methods of calculating tables.
Al-Khwarizmi is credited with developing the algorithmic concept for solving problems. In his work, he emphasized on the use of logical steps to solve mathematical problems. Al-Khwarizmi proposed rules that were to be followed when solving mathematical equations. The Biography Base reports that Al-Khwarizmi made use of logic to solve linear equations (par. 3). He surmised that the person could arrive at the right answer by using the step-by-step procedure stipulated. This step-by-step approach of solving problems has been exploited in the 20th century by computer scientists.
Astronomy
In addition to mathematics, Al-Khwarizmi made significant contributions to the field of astronomy. He compiled elaborate astronomical tables that became standards in the field of astronomy. The astronomical handbook with tables (referred to as an Islamic zij) was of great value to Islamic and Western Astronomers. This compilation was made around 844 AD and it became an important reference resource for later astronomers (Hamid-Reza 504).
These tables incorporated a lot of material from Indian astronomy studies (Berggren 13). Indian astronomy contained mathematical formulae that related angular diameters of the sun and the moon with their angular velocities (Hamid-Reza 503). This critical knowledge was transferred to the astronomy of the Islamic period through Al-Khwarizmi’s work. In addition to the Indian works, Khwarizmi’s tables included numerous methods from the Greek and Iranian pre-Islamic astronomy. Al-Khwarizmi’s astronomical methods, which were mostly based on Indian astronomy, were the first such works to reach the west. Here they gained a wide audience and were translated into Latin even further increasing their audience. Prominent West astronomers such as Maslama of Madrid made use of Al-Khwarizmi’s work to advance astronomy studies.
Impact of Al-Khwarizmi’s Work
Al-Khwarizmi’s treatise on Algebra was translated into Latin in 1140 and it went on to have great influence on European scientific development. His book became a standard mathematical text at European institutes where the discipline of algebra, as introduced by Al-Khwarizmi, was taught (Syed par. 12). The modern word “algebra” comes from his book “Hisab Al-Jabr W Al-Muqabala” which translates as “The Compendious Book on Calculation by Completion and Balancing” (Syed par. 3).
The information contained in the treatises was of a revolutionary nature and it signified a new development in algebraic thought. Even though Al-Khwarizmi’s work did not make use of the modern symbols of algebra, it was highly practical and an obvious advancement in medieval algebra. Ofek states that Al-Khwarizmi’s research in algebra is the foundation on which the modern day algebraic system is based (6). Mathematicians in subsequent decades were able to use Al-Khwarizmi’s work to develop the modern algebraic system.
Discussion and Conclusion
This paper set out to provide a report on one of the most renowned Mathematicians of the Medieval Era, Al-Khwarizmi. The paper started by providing a brief history of his life. It highlighted how he moved to Baghdad and served as an astronomer for Caliph Al-Mamun’s court. Due to his position in the court, he was able to regularly access the House of Wisdom and gain knowledge from various parts of the world. The paper then delved into the significant works done by Al-Khwarizmi’s in mathematics. It noted that Al-Khwarizmi’s work in mathematics was revolutionary and it is considered a cornerstone of science. For this reason, this medieval scientist is regarded as the father of Algebra and the father of computer science.
The paper notes that in addition to synthesizing Greek and Indian knowledge to aid in the advances of Mathematics and Astronomy, Al-Khwarzmi was able to make his own original contributions, which were of great importance to science and mathematics. His work had a great impact on the West and it is credited with having played a part in the Scientific Revolution in Europe. Al-Khwarizmi’s contributions to modern science and mathematics continue to be appreciated many centuries after his death.
Figures and Explanations
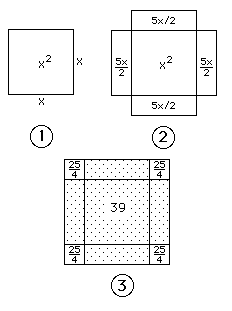
x2 + 10x = 39
Al-Khwarizmi explains
.. Square and 10 roots are equal to 39 units. The question therefore in this type of equation is about as follows: what is the square which combined with ten of its roots will give a sum total of 39? The manner of solving this type of equation is to take one-half of the roots just mentioned. Now the roots in the problem before us are 10. Therefore take 5, which multiplied by itself, gives 25, and an amount which you add to 39 giving 64. Having taken then the square root of this which is 8, subtract from it half the roots, 5 leaving 3. The number three therefore represents one root of this square, which itself, of course is 9. Nine therefore gives the square.
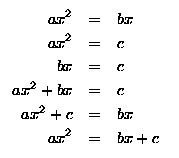
Al-Khwarizmi stated that any linear or quadratic equation could be reduced to one of the above forms. This reductions are done using the processes of completion and balancing. By completion, the negative terms in the equation are removed successively. In balancing, the positive terms on the two sides of the equation are reduced if they are of equal power.
Works Cited
Berggren, John. “The Joint Journey of Mathematics and Astronomy in the Ancient World.” IP Conference Proceedings 1283.1 (2010): 1-17. Web.
Biography Base. Al-Khwarizmi Biography. n.d. Web.
Hamid-Reza, Giahi. “Al-Khwarizmi and Annular Solar Eclipse.” Arch. Hist. Exact Sci. 65.1 (2011): 499-512. Web.
Hazmy, Wan, Zainurashid Zainuddin and Hussaini Mohamad. Muslim Scholars and Scientists. Negeri Sembilan, Islamic Medical Association of Malaysia N. Sembilan, 2005. Print.
Ofek, Hillel. “Why the Arabic World Turned Away from Science.” The New Atlantis 3.1 (2011): 3-23. Web.
Sayili, Aydin. Al-Khwarizmi, Abu’l-Hamid Ibn Turk and the place of Central Asia in the History of Science and Culture. Manchester: Foundation for Science Technology and Civilization, 2006. Print.
Shafiq, Alvi and Al-Roubaie Amer. Globalization of Knowledge: Islam and Its Contributions. Manchester: Trafford Publishing, 2011. Print.
Syed, Ibrahim. Al-Khwarizmi-the Father of Algebra. 2010. Web.