OleT Enzyme Engineering to Improve Biofuel Yield Dissertation

Abstract

The increasing demand for fuel coupled with dwindling fossil fuel reserves has created anxieties regarding a looming global energy crisis. Thus, there is an increased interest in the use of biofuels, which are sustainable fuel sources with minimal environmental concerns. Biofuels such as terminal alkenes can be produced from fatty acids in microbial systems such as OleT_JE, a unique variant of cytochrome P450. However, the reaction machinery results in undesired α- and β-hydroxylation by-products, which reduce the yield of terminal olefins.

The purpose of this project was to use a simplified density functional theory (DFT) model, quantum mechanics (QM), and molecular mechanics (MM) to engineer OleT_JE to overproduce terminal olefins by eliminating these hydroxylation by-products. Starting samples were obtained from the protein databank in PDB format. The geometry of the reactant complex was optimized and scanned to find the lowest energy pathway to bond hydrogen and oxygen atoms of abstraction of the closest hydrogen from the alpha and beta carbons in the triplet and quintet states. The geometry of the transition for the beta carbon was also optimized and scanned to elucidate the decarboxylation pathway.

Energy barriers for each step were recorded. There were minor differences in the geometries and energy differences of the triplet and quintet transition states following hydrogen abstraction from C_α and C_β positions. However, abstraction from the quintet state had higher barrier energy than the triplet state. The decarboxylation transition state via Cpd I was significantly lower notwithstanding the spin state. The findings led to the conclusion that the overall reaction rate to increase olefin yield was faster on the triplet state due to the relatively lower transition state for hydrogen abstraction from the beta carbon_.

Introduction

Global energy demand is reported to have increased significantly over the last year. The Global Energy and CO₂ Status Report (released in March 2018) indicated that energy requirements all over the world have increased by a margin of 2.1% in 2017, which was more than double the amount of the previous year (International Energy Agency 2018). This increase was attributed to a boost in economic growth all over the world. Approximately 70% of the energy demands were met by gas, coal, and oil, whereas renewable energy sources accounted for the rest of the demand. The rapid

increase in global fuel consumption has led to many concerns regarding dwindling fuel reserves. This problem is made worse by volatile geopolitical factors, the inconsistent cost of fossil fuel, and increasing apprehensions about national energy security (Covert et al. 2016). Moreover, the use of fossil fuel causes serious environmental concerns due to the emission of greenhouse gases (Nicoletti et al. 2015). The International Energy Agency (2018) reports that the increase in global energy use was associated with the emission of vast quantities of carbon dioxide gas, which is a known greenhouse gas. Carbon dioxide gas emissions increased by 1.7%, whereas carbon emissions rose to 32.5 gigatonnes, which was the highest level ever recorded.

Thus, these findings show that fossil fuel substitutes should be developed to protect the environment from the adverse effects of large quantities of carbon dioxide gas. Biological materials can be used to generate renewable sources of energy. Additionally, fuels from these sources do not cause adverse environmental consequences. Biofuels have been around for many years. Peanut oil was used to operate diesel engines in the early 20^th century (Guo, Song & Buhain 2015).

However, the discovery of cheaper fossil fuels shifted attention to their use thereby causing biofuels to be forgotten. Bioethanol and biodiesel are the most commonly used biofuels in the current market (Pulidindi & Gedanken 2015). Bioethanol is made by the fermentation of carbohydrates in a process that is similar to that of beer brewing as shown in Figure 1.

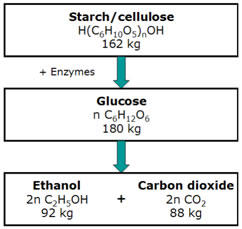
In recent years, bioethanol has been used as an additive to fossil fuels to minimize the production of carbon monoxide and other emissions that lead to the formation of smog (Shahir et al. 2015; Mofijur et al. 2016). For example, in the United States, ethanol from corn is added to gasoline (Chum et al. 2016). Additionally, flexible-fuel vehicles that can operate on mixtures of gasoline and high proportions of ethanol are now available.

Countries such as Brazil have been using ethanol from sugarcane as a biofuel and have cars whose engines can be powered using pure ethanol (Chum et al. 2016; Martins et al. 2018). Similarly, Europe produces biodiesel from palm oil for use in motor vehicle engines (Mathews & Ardiyanto 2015). Biodiesel is produced by mixing alcohol (in most cases methanol) with organic substances such as animal fat, and vegetable oil. The most common use of biodiesel is to decrease vehicle emissions. However, it can still be used as a renewable substitute fuel in its pure form in engines that use diesel.

Other forms of biofuel encompass methanol and reformulated gasoline constituents. Methanol, which is also referred to as wood alcohol, is mainly manufactured from methane or biomass. Examples of reformulated gasoline constituents include methyl tertiary butyl ether and ethyl tertiary butyl ether. These substitutes produce reduced amounts of pollutants as opposed to conventional fuels.

Nevertheless, the best biofuels are bio-hydrocarbons, particularly intermediate to long-chain fatty alkanes or alkenes (Liu et al. 2014). Aliphatic hydrocarbons also serve other purposes such as polymers, detergents, and lubricants in industrial and domestic applications. These biofuels are preferred because of their close semblance to petroleum-based fuels concerning their chemical structures and physical attributes. Therefore, recent research efforts have focused on the biosynthetic pathways of biofuels from different microorganisms as well as their potential in the production of aliphatic hydrocarbons (Liao et al. 2016; Zargar et al. 2017).

One benefit of using microorganisms to synthesize fatty alkanes or alkenes is that microbial systems are can be scaled appropriately based on the quantities of the desired products. Consequently, microbial systems are cost-effective.

The production of biofuels in microbial systems is a biological process that involves biological reactions, which require enzymes. Enzymes are biological catalysts that speed up the rate of biochemical reactions. Living organisms produce enzymes naturally to expedite the conversion of substrates to useful products that play various roles in different physiological functions. A typical enzyme reaction involves the attachment of the substrate to the reaction center of the enzyme, which results in the creation of an enzyme-substrate complex (Cornish-Bowden 2014).

Thereafter, an intricate series of chemical reactions lead to the rearrangement of chemical bonds in the substrate, which leads to the formation of a product. Naturally occurring enzymes are highly efficient in their various roles at biological temperatures and pressures by reducing the rate of reactions substantially. Then again, experimental conditions differ from physiological ones, which interfere with the catalysis of the enzyme outside biological systems. As a result, rigorous research is in progress to elucidate the properties and machinery of biological enzymes to facilitate the exploitation of biocatalysts in the chemical industry.

However, such endeavors have been frustrated by the nature of enzyme-catalyzed reactions, which are too fast for investigators to obtain accurate details that would be beneficial for comprehending the machinery and reaction pathways. Therefore, novel computational techniques have been developed leading to the creation of accurate models that can envisage the reactions of biocatalysts. Thus, it is now possible to examine large biochemical systems.

Investigations concerning the production of biofuel in microbial systems have shown the involvement of a special group of enzymes known as cytochrome P450 alongside heme enzymes. Cytochrome P450 is an important group of enzymes whose main purpose is to metabolize drugs in the human body (Liu et al. 2014). These enzymes are ubiquitous in living organisms, including plants, fungi, bacteria, and eukaryotic organisms (Nelson 2018).

Different subclasses of cytochrome P450 have been characterized based on their involvement in different biological functions. A heme enzyme reacts with fatty acid substrates in a reaction that involves a decarboxylation step mediated by a cytochrome P450 peroxygenase. This scheme can synthesize biofuel (Grant et al. 2015). However, it liberates several by-products that must be removed from the desired product before it can be used. Currently, most investigative efforts report 50% decarboxylation and 50% hydroxylation products in the production of biofuels by cytochrome P450 (Faponle et al. 2016). Therefore, there is a need to engineer the protein to enhance the yield of biofuel.

The use of quantum mechanics or molecular mechanics (QM/MM) techniques has facilitated the characterization of biochemical systems by researchers. Quantum-mechanical (QM) approaches fall into ab initio methods that entail the computation of a system devoid of prior knowledge (de Visser et al. 2014). Overall QM methods work by working out the Schrödinger equation. As much as QM methods can expedite the accurate computation of systems, their requirements increase based on the number of atoms or electrons in the system. Therefore, these methods are unbefitting for investigations involving enzymatic systems (de Visser 2009).

In contrast, alternative methods such as molecular mechanics (MM) that can deal with systems with a higher number of atoms are unable to expound bond-breaking or formation processes. As a result, innovative techniques that amalgamate the rapidity of MM with the exactitude of QM have been developed, leading to computational procedures that can give details of enzymatic systems. One such method is based on the density functional theory (DFT) alongside high computational power, which has led to increased interest in theoretical chemistry processes.

DFT computations are usually executed to provide backing for experimental biochemical and inorganic investigations, facilitate the interpretation of data, and give directions for new experiments. This dissertation aimed at reviewing the use of the OleT enzyme in biofuel production to determine existing gaps, engineering the enzyme to improve its yield, and reporting the findings of the investigation.

Project Objectives

The project aims to engineer the OleT enzyme to improve its biofuel yield.

The objectives include:

• Using computational methods to design and develop mutants that give a higher yield of biofuel products.
• Discussing the outcomes of the computational endeavors and their application in practical settings.
• Discussing the expected personal, academic, industrial, societal, and economic benefits of the project.

Literature Review

Production of Biofuels

To this point, four bacterial biosynthetic pathways that convert free fatty acids into hydrocarbons have been identified and exemplified. The first pathway, which was identified in cyanobacteria, is made up of two enzymes: an acyl-acyl carrier protein (acyl-ACP) reductase and an aldehyde decarbonylase (Choi & Lee 2013; Wang, Liu & Lu 2013). These two enzymes convert fatty acyl-ACPs to alkanes (Liu et al. 2014). The second pathway comprises a cluster of three genes in Micrococcus luteus, which catalyze the head-to-tail linkage of two fatty acyl-coenzyme A (acyl-CoA) molecules to form alkenes with internal double bonds (Chen et al. 2015).

The third reaction path uses a unique P450 decarboxylase OleT_JE, which was isolated from Jeotgalicoccus sp. ATCC 8456 (Grant et al. 2015; Hsieh et al. 2017; Matthews et al. 2017a). OleT_JE catalyzes the direct removal of carbon dioxide molecules (decarboxylation) from long-chain fatty acids to produce α-olefins (Liu et al. 2014). This reaction occurs in the presence of H₂O₂. The fourth reaction uses a type I polyketide synthase isolated from Synechococcus sp. PCC 7002 (Lin et al. 2015). This enzyme uses five consecutive steps to transform fatty acyl-ACPs into α-olefins (Lennen & Pfleger 2013; Mendez-Perez, Herman & Pfleger 2014).

Out of the four methods, the simplest reaction is the one-step decarboxylation of fatty acids by OleT_JE P450. Besides, this enzyme can use different molecules as substrates, for example, free fatty acids as substrates in the place of fatty acid thioesters. The ability of OleT_JE P450 to use free fatty acids as substrates is considered an advantage in metabolic engineering because free fatty acids are abundant in nature (Faponle et al. 2016).

Also, free fatty acids are easily manipulated in microorganisms such as E. coli, which is one of the most highly developed microbial cell industrial units (Chen et al. 2013; Marisch et al. 2013; Rosano & Ceccarelli 2014; Wang & Zhu 2018). Hence, OleT_JE P450 fatty acid decarboxylative mechanism holds immense potential for engineering into a biological α-alkene-producing scheme.

Cytochrome P450 Enzymes

Cytochrome P450 is a superfamily of heme-containing external monooxygenases (Faponle et al. 2016). The name of this group of enzymes is attributed to their categorization as hemoproteins (proteins that contain heme as a cofactor) and an exhibition of distinct spectral features. P stands for pigment, whereas the term 450 signifies the rare absorption peak of the reduced CO-bound compound at a wavelength of 450 nm. Cytochrome P450s play a crucial role in the metabolism of drugs in humans, particularly in phase 1 reactions where drug molecules undergo various reactions to render them water-soluble (Faponle et al. 2016).

The cytochrome P450 enzyme group is very diverse. Molecular investigations indicated that more than 20,000 distinct sequences of the enzyme had been identified as of January 2015 (Belcher et al. 2015). In humans, the site where cytochrome P450s are found predominantly is in the liver where they catalyze the breakdown of toxic substances (Zanger & Schwab 2013; Rendic & Guengerich 2014; Ji et al. 2015).

However, these enzymes also play a role in other physiological processes such as the biosynthesis of hormones, degradation of vitamin D, metabolism of alkaloids, steroids, eicosanoids, and fatty acids, the formation of bile acid, as well as the instigation of procarcinogens (Nebert, Wikvall & Miller 2013). These processes demonstrate the diverse roles of cytochrome P450s in the body and their versatility in the activation of substrates. In plants, cytochrome P450s play a central role in the metabolism of herbicides and secondary metabolites (Renault et al. 2014; Saika et al. 2014; Zhai et al. 2014).

The identification of more than 20,000 forms of cytochrome P450 as well as the diverse physiological functions of the enzyme implies that it has different isoenzymes (isozymes) in organisms that use it (Gricman, Vogel & Pleiss 2014). Isozymes are enzymes that exist in different molecular forms within the same organism. The substrate-binding pocket of P450 differs in shape and size in its various isozymes. The functional group of cytochrome P450 enzymes is made up of an iron (IV)–oxo heme cation radical moiety that is referred to as Compound I (Faponle et al. 2016). The characterization of Compound I (Cpd I) can provide valuable data regarding the mechanism of cytochrome P450.

However, the experimental exploration of Cpd I is convoluted by its transitory nature, which constrains the availability of information about its catalytic machinery. Theoretical and experimental investigations reveal that the most common reaction mechanism executed by the cytochrome P450 enzymes is the aliphatic hydroxylation of substrates. Empirical studies have shown that aliphatic hydroxylation is a stepwise sequel that forms alcohol compounds as the main products.

Furthermore, this mechanism has been substantiated by computational modeling, which has revealed that the oxidation state consists of two spin states (lying close to each other) that yield two-state reactivity configurations, each having its rate constant (de Visser et al. 2014). The two-state reactivity prototype also projects that the lifespan of the radical intermediary could lead to a split of the potential energy. Cytochromes P450 takes part in catalytic reactions, for instance, dehalogenation, peroxidation, hydroxylation, sulfoxidation, S-dealkylation, desulfuration, and epoxidation, among many others (Zhao et al. 2014).

During these reactions, the enzyme needs to interact with its corresponding electron donors. This interaction is crucial because it confers enzyme specificity, which ensures adequate catalysis and acceptable reaction rates while guarding the system against side reactions.

The cytochrome P450 enzyme superfamily is among the most flexible naturally occurring biocatalysts. These enzymes use oxygen to catalyze their reactions. Electron-moving proteins transfer electrons to the enzyme to accelerate the activation of oxygen, whereas the electron carriers NADH or NADPH smooth the progress of substrate hydroxylation. Most cytochrome P450 variants are bound by membranes and have different hydrophobic substrates where they catalyze monooxygenation reactions.

Some of the substrates involved in these reactions include biological compounds such as steroids, fatty acids, and prostaglandins. On the other hand, extraneous compounds that take part in monooxygenation reactions include organic solvents, ethanol, anesthetics, and alkyl aryl hydrocarbon products. In monooxygenase reactions, one or more redox affiliate proteins are used to convey two electrons from NADH or NADPH to the heme iron in the reactive center of the enzyme for dioxygen initiation. Subsequently, one atom of oxygen is inserted into their substrates during catalysis.

This reaction mechanism has led to the naming of the enzymes as P450 monooxygenases. A typical cytochrome P450 catalytic cycle is shown below in Figure 2. The reaction begins with the P450 “latent” state having a ferric (Fe³⁺⁾ heme iron axially coordinated by cysteine thiolate (S) and a weakly bound water molecule (H₂O). The association of OleT_JE with H₂O₂ generates a volatile iron-oxo species that undergoes protonation and dehydration producing compound I. From this point, either fatty acid decarboxylation or hydroxylation can occur.

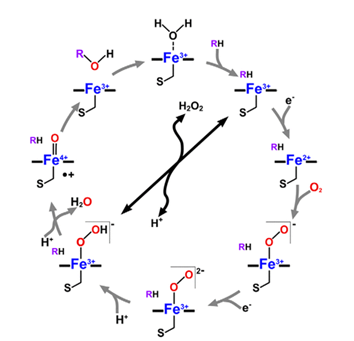
However, an exceptional cytochrome P450 family, the CYP152 family, includes members that rely on H₂O₂ solely as the only electron and oxygen donor. These members are known as P450 peroxygenases and they include P450_SPα, P450_BSβ, and OleT_JE (Matthews et al. 2017a). The peroxygenase activity of P450 enzymes is usually considered an advantage in practical settings due to the cost differences between H₂O₂ and NADPH.

H₂O₂ is significantly cheaper than NADPH and redox proteins. The applications of the peroxygenase activity of cytochrome P450 enzymes include catalytic reactions involved in the biosynthesis of biological molecules as well as enzyme additives in laundry cleansing agents (de Visser 2009). Therefore, there is an increased interest in taking advantage of the oxidative role of cytochromes P450 for industrial purposes.

A significant reaction mechanism in the chemistry of cytochrome P450 enzymes is the desaturation of aliphatic compounds to produce olefins (Munro et al. 2018). Desaturation reactions bear numerous similarities to aliphatic hydroxylation because both processes start with the elimination of a hydrogen atom from the substrate (Ji et al. 2015). Nonetheless, the reaction subsequently divides into two possible product routes the first of which presents OH rebound to form alcohol products, whereas the other path leads to the elimination of a second hydrogen atom to produce an olefin and water (Matthews et al. 2017a).

The first reaction pathway is referred to as aliphatic hydroxylation while the second path is known as desaturation. Desaturation reactions are of immense interest in the production of biofuels from organic substances (Ghosh et al. 2016; Hendry et al. 2016; Carvalho et al. 2017). Even though comprehensive scientific investigations into the chemistry of P450 have been conducted for decades, many gaps exist in the understanding of its reaction mechanism. For example, there is inadequate information regarding the intricate details of its hydroxylation and desaturation mechanisms as well as possible ways of bioengineering these reaction pathways to produce a specific product.

Cytochrome P450 Peroxygenase OleT_JE

Peroxygenases are cytochromes P450 that make use of the peroxide shunt mechanism to catalyze the hydroxylation of long-chain fatty acids to produce alcohol (Beller, Lee & Katz 2015; Wang et al. 2017). Adding hydrogen peroxide or any other organic peroxide to the reaction medium facilitates the production of compound 0 or compound I without the need for expensive redox partners such as NADPH and NADH. The CYP152 family contains the most important cytochrome P450 peroxygenases (Hsieh & Makris 2016; Matthews et al. 2017b). A notable peroxygenase is cytochrome P450 peroxygenase OleT_JE, which was isolated from Jeotgalicoccus sp. ATCC 8456 (Fu et al. 2015; Lee et al. 2015).

OleT_JE catalyzes the unusual decarboxylation of long-chain fatty acids leading to the formation of α-alkenes in a reaction that uses H₂O₂ as the only electron and oxygen donor. An alternative reaction mechanism entails the use of an enzymatic redox cascade in addition to molecular oxygen and the recycling of NAPDH as shown in Figure 3.

Even though the decarboxylase activity of OleT_JE proceeds with relative ease, the industrial manufacture of cheap α-alkene biofuels on a large scale while depending on the H₂O₂-dependent enzymatic system is not feasible. The limitations of this reaction are attributed to the need for large quantities of hydrogen peroxide, which would be costly. Also, long-term exposure of biocatalysts to high concentrations of H₂O₂ is detrimental to their integrity and would lead to the inactivation of the enzymes. For these reasons, the H₂O₂-independent action of OleT_JE is ideal for the commercial production of α-alkenes in microbial systems (Liu et al. 2014).

Aliphatic α-alkenes are valuable because of their potential use as biofuel substitutes for fossil fuels, manufacture of lubricants, detergents, and polymers (Pai et al. 2017). Therefore, studies on fatty acid decarboxylation by OleT_JE are important and findings from such studies can inform the industrial manufacture of biogenic α-alkenes, which are renewable and environmentally friendly fuel sources.

H₂O₂-Independent Activity of OleT_JE

H₂O₂-independent decarboxylation of fatty acids by OleT_JE occurs in vivo in the presence of NADPH and O₂ (Hsieh et al. 2017). Under these conditions, the OleT_JE enzyme efficiently decarboxylates long-chain fatty acids (fatty acids with carbon atoms ranging from 12 to 20) to produce terminal olefins. This process requires OleT_JE to work alongside a fused P450 reductase domain RhFRED from Rhodococcus sp., CamA, CamB, or a separate flavodoxin/flavodoxin reductase from E. coli (Zhou et al. 2018).

The uncovering of the H₂O₂-free activity of OleT_JE queries the monooxygenase-like machinery of the peroxygenase and directs future metabolic engineering efforts to enhance redox partners for efficient production of α-alkenes by OleT_JE. However, the reaction liberates appreciable quantities of α- and β-hydroxylation by-products whose origin is not clear (Faponle et al. 2016). The peroxide independent activity of OleT_JE shows potential in the production of biofuels because it does not pose a threatening environment for microbial systems as opposed to the peroxide-dependent pathway that destroys the integrity of microbial systems.

α- and β-Hydroxylation by-products of OleT_JE

QM/MM inquiries into the bifurcation pathways have facilitated the identification and elucidation of the formation of three by-products of OleT_JE. These studies have also made it possible for researchers to demonstrate how the enzyme can be engineered for peak desaturase activity. QM/MM investigations show that the availability of a substrate as well as the polarity of the solvent that is present in the binding cleft of the enzyme destabilizes the OH-rebound path and permits a thermodynamically disadvantageous decarboxylation reaction through kinetic means as shown in Figure 4 (Faponle et al. 2016).

Substrate Specificity of OleT_JE Systems in Peroxide-Independent Pathways

The enzyme-substrate affinity of different OleT_JE systems indicates the substrate preference of various OleT_JE systems to improve the comprehension of the in vivo mechanism of fatty acid decarboxylases (Grant, Mitchell & Makris 2016; Xu et al. 2017). This information also points out the metabolic engineering of fatty acid biosynthesis on the right track. Several straight-chain saturated fatty acids with even numbers of carbon atoms in the hydrocarbon chain have been used to resolve the substrate specificity of different OleT_JE systems. Liu et al. (2014) used long-chain fatty acids ranging from C₈ to C₂₀ to establish the substrate specificity of OleT_JE and OleT_JE-RhFRED.

The proportion of the substrate that was converted into the expected α-alkene product was used as an indication of the enzyme system’s substrate preference. Liu et al. (2014) noted that OleT_JE had the highest preference for myristic acid (C₁₄) for olefin production with approximately 97% of the fatty acid being transformed into terminal olefins. The proportions of lauric acid (C₁₂) and palmitic acid (C₁₆) that were converted to terminal alkenes were lower than the expected levels. OleT_JE could only transform small quantities of stearic acid (C₁₈) and arachidic acid (C₂₀) to alkenes (Figure 5). However, the enzyme could not catalyze the decarboxylation of capric acid (C₁₀) or caprylic acid (C₈).

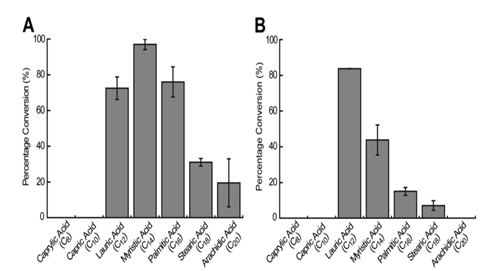
On the other hand, it was demonstrated that the OleT_JE-RhFRED system had a higher affinity for fatty acids with relatively short chain lengths. This finding implied that the presence of a P450-reductase induced a small structural modification in the active site of OleT_JE. The highest activity for OleT_JE-RhFRED was shown for lauric acid at a conversion rate of 83.8%. Nevertheless, no activity was observed for arachidic, capric, and caprylic acids (Li et al. 2014).

Another outstanding observation was that the system consisting of OleT_JE-RhFRED, NADPH, and O₂ demonstrated a lower activity than OleT_JE and H₂O₂ for all fatty acids tested except lauric acid. The observed phenomenon indicates that OleT_JE could have evolved to augment its peroxygenase activity.

On the other hand, Dennig et al. (2015) established the enzymatic oxidative decarboxylation of short-chain fatty acids ranging from C₄ to C₉ using OleT, O₂ as the oxidant, and NAD(P)H as the electron donor to produce the corresponding terminal C₃ to C₈ alkenes. Product titers of up to 0.93 gL^-1 and total turnover numbers exceeding 2000 were given off. The development of a well-organized electron-transfer series using putidaredoxin CamAB together with the reutilisation of NAD(P)H without regard for the formate, glucose, or phosphite made it possible for these yields to be attained (Dennig et al. 2015).

Even though CamAB could oxidize NAD(P)H without an appropriate electron acceptor, no H₂O₂ was detected after the full oxidation of 1 mm NADH, which indicated the likelihood of a direct electron displacement from CamAB to OleT. This observation also ruled out the possibility of inactivation by hydrogen peroxide. Consequently, the absence of catalase did not affect the throughput of the system. Astoundingly, fatty acids with short chains (fatty acids with carbon atoms ranging from C₄ to C₁₁) were decarboxylated, which resulted in the production of 0.04 to 2.45 mm of terminal alkenes.

The existing temperatures and the number of carbon atoms in the fatty acid chains affected the overall yield of the terminal alkenes. The highest activity of the enzyme was recorded for a C₁₈ fatty acid at room temperature, whereas C₁₂ yielded the best outcome at 48°C (3.26 mm of 1-undecane).

On the whole, high conversion rates were recorded for fatty acids ranging from C₁₀ to C₁₆ at temperatures of 48°C. The CamAB-OleT_JE system facilitated the production of propene from butyric acid in only one step. This observation disproved the previous hypothesis that OleT had a preference for long-chain fatty acids compared to short-chain fatty acids (Dennig et al. 2015).

It was presumed that long-chain fatty acids interacted with the substrate pocket, whereas smaller substrates were held in the binding compartment as evident in correlated enzymes, for example, CYP_BSß. The low conversion rates of fatty acids with intermediate chain lengths (C₁₀ and C₁₁) were attributed to poor binding of the substrate on the active site of the enzyme (Dennig et al. 2015; Hammerer, Winkler & Kroutil 2018). Decarboxylation was the principal reaction, with approximately 86 to 99% selectivity in fatty acids C₁₈ to C₂₂.

The formation of α- and β-hydroxylated products was influenced by chain length and reaction temperature (Faponle et al. 2016). There was 62% α-/β-hydroxylation when fatty acids with 9 carbon atoms reacted at temperatures of 48°C. The observed harmony between CamAB and OleT was associated with similarities in the synchronization of the adjacent cysteine thiolate moieties in the ferrous states of OleT and P450Cam, which allowed the attachment of oxygen to the heme iron.

Most P450 enzymes of bacterial origin depend on class I electron-transfer schemes (Dennig et al. 2015; Liang et al. 2018), which explains the enhanced catalytic performance of OleT together with CamAB, as opposed to systems illustrated in the past such as OleT–RhFRed and Fdr/Fdx. These findings indicate that metabolic engineering efforts directed at the peroxide independent activity of OleT_JE should consider pairing the enzyme with CamAB to take advantage of different lengths of fatty acid substrates.

Product Distribution in OleT_JE Catalysis

Environmental effects may influence the branching and regioselectivity inclinations of enzymes. Therefore, Faponle et al. (2016) used QM/MM to study the full OleT_JE enzyme and investigate its bifurcation pathway and product distribution. The main objectives of the study were to identify the source of P450 OleT_JE product formation and predict the features that break up the decarboxylation from hydroxylation pathways.

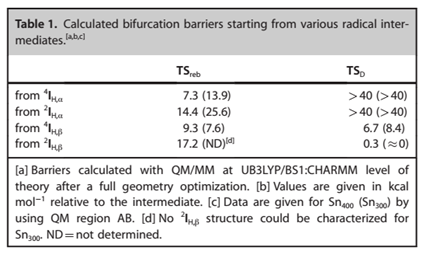
The findings revealed that were no significant changes in geometry, spin state collation, and comparative energies. Geometry studies showed that there were no substantial disparities between hydrogen-atom extraction impediments. In all instances, the hydrogen atom was nearly equidistant from the donor and acceptor atoms, notwithstanding the type of the QM region studied. It was evident that hydrogen atom removal impediments by Cpd I from the C_α and C_β loci of the substrate were close in energy on the doublet or quartet spin states. All four impediments fell within a range of 3.2 (BS1) or 4.0 (BS2) kilocalories per mole for Sn₄₀₀ (Faponle et al. 2016).

The observed hydrogen atom extraction impediments corroborate empirical findings of a combination of reaction outcomes from C_α and C_β hydrogen atom removal. The minor disparity in the entropies of the two reaction courses suggests that the chemical reactions that lead to the elimination of a hydrogen atom between C_α and C_β are competitive. However, the ratio of the C_α and C_β pathways as depicted by the comparative energies of the transitional state moieties ^4,2TS_HA,α, and ^4,2TS_HA,b were strongly influenced by environmental factors, for example, the associations between hydrogen bonds (Faponle et al. 2016).

The experiment by Faponle et al. (2016) showed that hydrogen atom extraction was the rate-limiting stage in the reaction mechanism. Therefore, the authors approximated a large kinetic isotope effect and computed an estimate for the substitution of hydrogen atoms by deuterium (molecular mass of 11). Geometry shots were also taken to determine possible hydrogen atom removal from the C_γ locus of the substrate (Sn₄₀₀). It was noted that the reaction energy exceeded the reactant complex by more than 30 kcal mol^-1 hence this mechanism was overlooked (Faponle et al. 2016).

The system slowed down following the removal of hydrogen atoms to form a radical intermediate (I_H,α or I_H,β) with an iron(IV)–hydroxo group and a reactive substrate on either the C_α or C_β locus of the substrate. The transitional species ^4,2I_H,α only reacted through radical rebound past the rebound transition state ^4,2TS_reb,α thereby leading to the formation of α-hydroxo arachidonic acid upshots (^4,2 P _OH,α). The rebound barriers recorded during the investigation were larger and higher in energy than is the norm for P450 hydroxylation reactions. Under normal circumstances, the low-spin pathway does not have any impediments. A decarboxylation reaction cannot take place following the removal of C_α hydrogen; it requires the additional removal of a hydrogen atom from C_β to C_α, which requires high energy.

The competitive pathways that resulted in decarboxylation and hydroxylation products (P_D,β and P_OH,β, correspondingly) via transition state TS_D,β, and TS_reb,β came from the radical intermediate ^4,2I_H,β, as estimated by snapshots Sn₃₀₀ and Sn₄₀₀. The high-spin pathway through ⁴ I_H,β gave rebound and decarboxylation hindrances that were almost similar in energy hence could be regarded as competitive. On the other hand, the low-spin path produced quality decarboxylation products from ²TS_H,β directly without stable radical intermediates.

These findings indicated that the rebound barriers were bigger than conventionally found in ideal complexes, which was attributed to numerous hydrogen-bonding connections to the iron–hydroxo group. These restrictions increased the obstacles to the rotation and rebound pathways. Besides, the hydroxylation process was dominant following C_α-H removal while decarboxylation was favored following the extraction of the C_β-H atom on the doublet spin state.

On the other hand, the surface of the quartet spin state was expected to liberate a mixture of products. This observation implies that the reaction should be modified to promote C_β-H extraction and impede C_α-H removal to promote decarboxylation. The elevated rebound barrier was linked to hydrogen-bonding interactions because of the water channel in P450 OleT_JE in addition to the polarity of the nearby carboxylate-Arg₂₄₅ salt bridge (Faponle et al. 2016). The importance of water channels in P450 OleT_JE was also demonstrated.

Bifurcation Pathways of OleT_JE

Faponle et al. (2016) used a valence-bond (VB) diagram to elucidate the bifurcation pathways of P450 OleT_JE (Figure 6). The illustration in Figure 6 shows that the wave function of the reactant (YI) merges with an energized state in the geometry of the yields, which is Y_reb* for the alcohol products and Y_D* for the decarboxylation output. The wave function of the product joins the energized excited state in the reactant geometry (^4,2I_H,β) in the same way.

The extent of the reaction inhibition is a function of the excitation energy needed to transform reactant to the product in the reactant geometry. Thus, the bifurcation machinery is determined by the comparative magnitude of the excitation energies G_reb or G_decarb (Faponle et al. 2016). Therefore, the microelectronic discrepancies between the wave functions in the ground and excited states regulate the barrier inhibitions and rate constants for the rebound and decarboxylation reactions.

Evaluating the VB structures in the geometry of ^4,2I_H,β with emphasis on the ground and excited states clarify the parameters that govern the bifurcation variables. For OH rebound and the development of hydroxylation outcomes, the π_yz/π*_yz set of orbitals was divided into two atomic orbitals, 3d _{yz, Fe} and 2p_{y, O}. The division of orbitals process expended an estimated E_π/π*yz in energy from the system, which was estimated at 37.2 kcal mol^-1.

The 2p_{y, O} orbital coupled with Φ_Sub, a substrate radical, to create the C-O bond orbital (σ_C-O) in a process that consumed a bond severance energy BDE_CO of 87.2 kcal mol^-1. On the other hand, since the 2p_{y, O} had a double occupancy in ^4,2I_H,β, it was imperative to upgrade one electron to a free low-lying orbital. The two available orbitals were 3d_xz in the doublet spin state and the σ*_z2 orbital in the foursome spin state, E_exc. The excitation energy was approximated at 75.3 kcal mol^-1. Thus the value of G_reb was predicted as 25.3 kcal mol^-1. As a rule, the height of the barricade is usually 33.33% of the promotion gap, which implied that a rebound barrier of approximately 8 kcal mol^-1 was applicable.

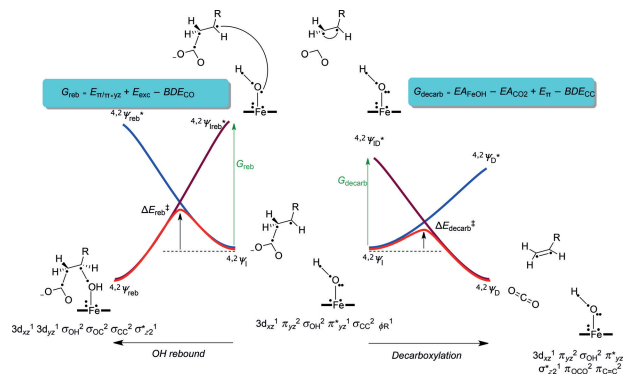
However, a different scenario was witnessed in the decarboxylation reaction where two processes occurred simultaneously. The C-C_α bond of the substrate disintegrated (BDE_CC) while the leaving CO₂^– group was oxidized to CO₂. The second process denoted the electron affinity of CO₂ (EA_CO2). As a result, the electron duo in the C-C_α orbital (σ_CCα) was split, after which the electron on C_α coupled up with the reactive group on C_β to create a π bond (π _CαCβ) possessing energy E_π.

The additional electron was taken up by the iron–hydroxo compound, which was reduced by an amount of energy that corresponded to its electron affinity (EA_FeOH). The electron affinity of the iron complex was estimated at 56.5 kcal mol^-1, whereas the strength of the C-C bond in the substrate, BDE_CC, was found to be 7.8 kcal mol^-1 (Faponle et al. 2016). Conversely, the singlet to triplet energy gap was used to compute the energy of the π bond, which yielded a value of 73.7 kcal mol^-1.

A promotion gap for decarboxylation (G_decarb) of 3.4 kcal mol^-1 was computed using the standard electron affinity of CO₂ (‑0.60 eV). The findings pointed towards a minor reaction barrier that was estimated to be less than 1 kcal mol^-1. Figure 7 indicates the calculated bifurcation impediments of different radical intermediates.

Factors Affecting Decarboxylation Reactions of OleT_JE

It is necessary to ascertain the factors that influence a reaction path that leads to the formation of the desired product before designing an enzyme to overproduce a given product. Investigations indicate that the decarboxylation pathway of OleT_JE is mainly influenced by substrate factors (Xu et al. 2017). These aspects include the intensity of the C-C_α bond, the energy required to create the π bond between C_α-C_β, and the electron affinity of CO₂ (Faponle et al. 2016; Fang et al. 2017).

The effect of the oxidant on the decarboxylation reaction is only felt through the electron affinity of the iron (IV)–hydroxo moiety. Consequently, boosting the regioselectivity of decarboxylation as over the hydroxylation activity should focus on weakening the hydroxylation path by engineering the substrate-binding compartment or using alternate substrates. The computations presented by Faponle et al. (2016) show that the substrate-binding compartment of P450 OleT_JE is highly polar and has numerous hydrogen-bonding interactions, which are crucial to the disruption of the radical rebound reactions that lead to the formation of α- and β-hydroxo fatty acids.

Also, electron-extracting moieties attached to the C_α or C_β locus would elevate the energy required to form the C-O bond, which would increase the radical rebound barriers. In contrast, the decarboxylation reactions would be boosted further by using substrates with an alkene bond between C_γ and C_δ. Such substrates would promote the π conjugation with the C_α-C_β π bond, thereby leading to increased E_π energy and stabilization of the decarboxylation process.

Theoretical Background of QM Simulations

Quantum mechanics proposes that the wave function can provide all attributes of a molecular system, which in turn solves the Schrödinger equation (McMahon 2013; Mohebbi, Abbaszadeh & Dehghan 2013; Edmonds 2016). The overall energy of a molecule is depicted as an eigenfunction of the Hamilton operator (H) as shown in equation 1 below.

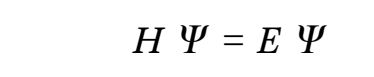
The Hamilton operator encompasses the kinetic and potential energy influences of all the electrons and nuclei within a molecule (Omnes 2018). This relationship is summarized by equations 2 and 3 where h denotes Planck’s constant, m_e is the mass of the electron, e is the charge of an element, ε₀ symbolizes the permittivity in a vacuum, and r_ij depict the expanse between. On the other hand, the spaces between two electrons and two nuclei are portrayed by r_ij and R_IJ, correspondingly. Consequently, the Hamiltonian in the second equation is divided into four constituents that exemplify critical components the first of which is the electrons’ kinetic energy. The other components include the attraction force between the electron and nucleus, the repulsive forces between electrons, and the repulsion force between two nuclei.

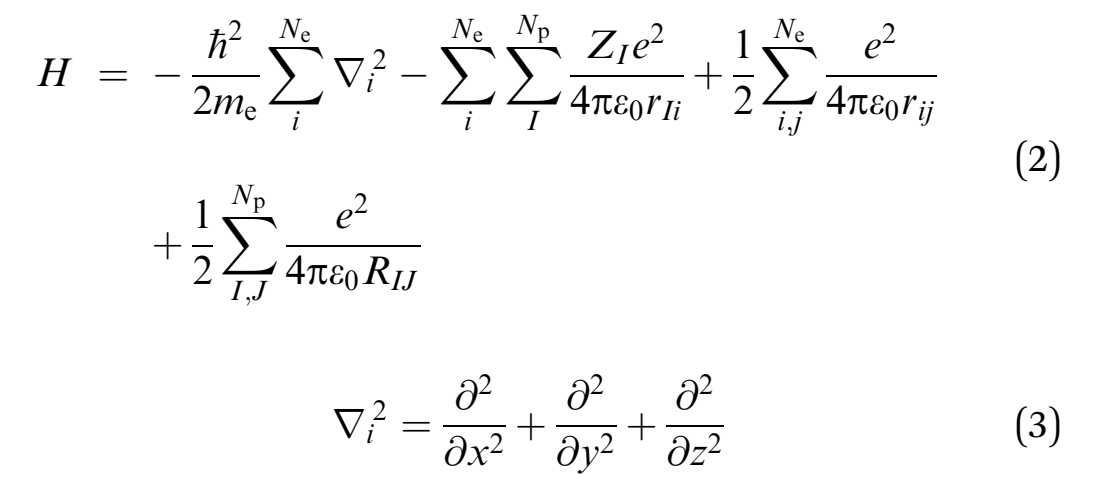
Therefore, elucidations of the Schrödinger equation are influenced by the total number of electrons and nuclei in a chemical system (Jensen 2017). These solutions increase in complexity as the size of the system increases (Harrison & Valavanis 2016; Le Roy 2017). The complexity of the Schrödinger equation implies that the equation can only be solved precisely for the hydrogen atom and ion. Estimations may be needed for larger chemical systems, which has led to the development of numerous computational chemistry approaches that encompass varying features and levels of precision (Alolyan & Simos 2015; Ning & Simos 2015; Grimme & Schreiner 2018).

On the whole, meticulous benchmarking and calibration are needed to produce accurate results, particularly for systems involving transition metals (Genheden et al. 2017; Mardirossian & Head-Gordon 2017). In such systems, the stability and reproducibility of techniques are ascertained by comparing findings to experimental data or advanced techniques.

Hartree–Fock (HF) theory provides the simplest solution to the Schrödinger equation (Koch & Holthausen 2015; Yanai et al. 2015). The assumption made is that every electron moves in the mean-field of other electrons. Therefore, one-electron wave functions are expanded into a group of known orbitals referred to as the basis set. Nonetheless, solving the Schrödinger equation does not imply that the computation is over but only provides the energy of the starting structure (de Visser et al. 2014). The geometry undergoes modifications followed by new computations. Subsequently, the energy is minimized about all geometric coordinates until the first derivatives of the energy reach a specific value. At this point, an optimized geometry is attained.

The HF technique provides reasonable geometries. However, its energies are insufficient to replicate chemical reaction machinery and experimental barrier heights. Coupled-cluster calculations using singles, doubles, and perturbatively treated triples (CCSD(T)) techniques are regarded as the gold-standard in QM (Sparta & Neese 2014; Calbo et al. 2015; Liakos & Neese 2015). The main disadvantage of these methods is that their computational demands make them relevant for simple systems with 50 atoms or less. Biomimetic complexes with 100 or more atoms require simpler computational methods (de Visser et al. 2014).

The density functional theory (DFT) was advanced in the 1960s as a substitute for the wave function approaches such as the B3LYP method (Obot, Macdonald & Gasem 2015). The electronic energy is computed as an unknown function of the electron density. The creation of functionals that rely on the electron density gradient led to major leaps in the DFT methodology and the development of semi-empirical methods. However, recent studies have highlighted the weaknesses of the B3LYP method, particularly with systems that include transition metals, thereby leading to the use of alternative DFT methods (Maxwell, Pendás & Popelier 2016; Medvedev et al. 2017).

However, no general and reliable method has been recommended. Therefore, researchers use different methods. Furthermore, HF and conventional DFT methods cannot explain dispersion interactions. A recent study has shown that correcting a simple empirical dispersion leads to a significant improvement in the energies computed using the B3LYP method. Therefore, it is necessary to validate DFT computations using experimental data.

QM computations provide the electronic energy of the system under investigation. However, these energies can be likened to experimental values by taking into account the effects of solvents, vibrations, and entropy. The extent of occupation of each vibrational energy level is determined by a Boltzmann distribution at a specific temperature. The specific partition functions for the translational, gyratory, and vibrational entropy constituents can be used to compute the overall entropy of the energy levels. Usually, the partial derivative of the free energy to the temperature at an invariable pressure is used to compute the entropy of a molecule. Quantum chemical software packages have these entropy derivations to estimate the free activation energy of a molecule, which can then be equated with experimentally derived values.

Computational chemistry approaches liberate energies that denote gas-phase data. Therefore, computational outcomes can only be compared with experiential findings following the incorporation of solvents into the computations. Therefore, it is necessary to add specific solvent molecules to the chemical model and re-optimize the structures. Nonetheless, introducing many atoms into the system complicates it and calls for complex computations that may not be feasible because solvent molecules exist in different conformations. Therefore, the most commonly used method entails the addition of solvent adjustments to the energetics with the aid of an implicit solvent model (Jensen 2017).

The QM/MM approach also makes it possible to incorporate the effects of the surrounding into QM computations. The guiding principle of QM/MM techniques is to split the chemical system into two or more distinct shells, which are referred to as the outer and inner cores as shown in Figure 8.

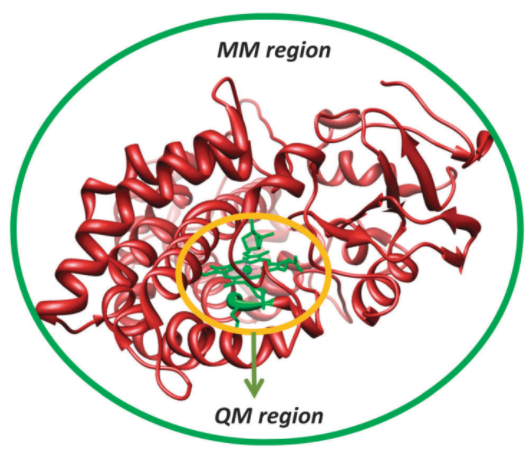
The computations of the inner core are implemented using precise QM or DFT techniques, whereas the calculations of the outer core that holds the rest of the protein and solvent are done using computationally inexpensive methods such as molecular mechanics. The inner core is of utmost importance because it holds the essential features of the substrate and the enzyme active site. The interactions of the inner core with other proteins hold it in position. These interactions maintain the conformation of the enzyme active site. Consequently, it is possible to blend the precision of QM methods with the rapidity of MM methods.

The literature review has provided useful insights that guide the engineering of OleT_JE to enhance its production of biofuels. The following insights have revealed that the enhancement of olefin product distributions requires site-directed mutations that impede α- and β-hydroxylation as well as altering the substrate-binding compartment to limit hydroxylation rebound reactions (Li et al. 2015). It is also evident that the choice of substrate, reaction temperature, and OleT_JE systems or combination of systems (Dennig et al. 2015) is critical in obtaining optimal terminal olefin yields from fatty acids. These pointers informed the computational methods in the methodology section of the project.

Methodology

Computational modeling of biosystems lays a basis for investigators to set up experimental inquiries because it excludes redundant variables that would otherwise be a waste of resources. The fact that quantum mechanics/molecular mechanics (QM/MM) techniques use computed reaction machinery and energy settings to provide details regarding the starting point of biological and chemical reactions, as well as their by-products, has increased the popularity of these methods over the years (de Visser et al. 2014).

As a result, researchers can collect data regarding factors that affect enzyme reactions, rates, and specificities by examining the different states of the molecules involved in enzymatic reactions. On the other hand, cluster replicas, for example, the Density Functional Theory (DFT) facilitate voluminous computations in a short span by probing precise features of a single protein (de Visser 2009; Jones 2015; Melander et al. 2016). Despite cluster models providing information about the intrinsic activity of enzymes’ active sites, there is inadequate information concerning intricate details such as key bonding patterns and lengths.

This section of the project provides a detailed procedure on the use of general QM/MM optimization protocols to promote the decarboxylation mechanisms of cytochrome P450 OleT_JE in the production of terminal olefins. The proposed elements of improvement as highlighted in the literature review were incorporated into the general QM procedure (Figure 8) to determine the most effective manipulations that would yield favorable outcomes.

QM/MM Methodology

The QM/MM method was initiated by finding heavy-atom coordinates of the protein (OleT_JE enzyme) from the protein databank library. These coordinates were available in a PDB format. As a result, the entire structure required editing as well as further adjustments before any simulations could be run. Examples of relevant modifications that were done to the initial PDB structure entailed the addition of hydrogen atoms, missing chains, substrates, and amino acid residues.

Another crucial modification was the removal of crystal additive buffers to leave the protein structure in its native state. The active site of the structure was also considered during the modifications. The resultant molecule was then solvated. These procedures made it possible to stabilize the system to encourage the correct folding of proteins. Snapshots that were required to execute the QM/MM simulation were then produced through a molecular dynamics (MD) simulation.

This process led to the split-up of the biochemical system into inner and outer cores. The computations of the inner core were completed using ab initio or DFT techniques that are reported to have high levels of accuracy (Lewars 2016). On the other hand, outer core calculations were achieved using MM approaches. These procedures have been validated using comparisons of experimental and theoretical data in various studies such as those conducted by Zeida et al. (2014), Wang et al. (2014), and Quesne et al. (2016). A sequential illustration of the specific steps of the QM/MM methodology is indicated in Figure 9.

Selection of Starting Structure in PDB Format

The accuracy and precision of QM/MM studies are dependent on the suitability of the starting materials. Therefore, researchers ought to be cautious when choosing the initial crystal structure from the protein databank. The ideal starting structure was not readily available from the protein databank. Most PDB files in the PDB database contained information indicating whether the structure was incomplete and whether any residues were missing.

As a result, modifications were unavoidable. However, the most comprehensive structure that contained many of the atoms in their correct positions was chosen to cut down the time required for modifications. Thus, the student ascertained the nature of the missing attributes (determined whether they were protein side-chains, loop areas, substrates, binding proteins, co-factors, or reducing partners) and selected the file with the closest semblance to the preferred structure.

This procedure also minimized the likelihood of errors during the modification of the structure. Another useful factor that was considered during the selection of the starting crystal structures was the resolution of the PDB files. Files with high resolution were preferred to those of low resolution because it was easier to identify distinct atoms as well as their location in the crystal structure. Therefore, PDB files with a minimum resolution of 2 Å were selected for the subsequent analyses. Besides, the investigator chose files with Rfree values of 0.3 or lower to ensure that only reliable structures were selected.

Modification of the Starting Structure

QM/MM computations of fast reactions provide the most informative data on enzymatic reactions. However, the pace of these reactions and their corresponding short-lived intermediates complicate the process of finding their crystal coordinates. This problem is usually circumvented by modifying a structure that is closely related to the target reaction. Therefore, a previous structure in a resting state was taken and modified appropriately.

Pertinent modifications of the starting structure were informed by the findings and recommendations of Quesne et al. (2016). These changes included involved substrate modification and alteration of the enzyme’s active site. Faponle et al. (2016) recommended that to augment the regioselectivity of decarboxylation reactions of OleT_JE as opposed to hydroxylation reactions, it was necessary to emphasize destabilizing the hydroxylation path by engineering the substrate-binding compartment. Another viable option was to use alternate substrates, which would bind the active site without leading to product formation thus inhibiting the formation of hydroxylation products.

The computations presented by Faponle et al. (2016) presented adequate calculations demonstrating the high polarity of the substrate-binding compartment of P450 OleT_JE, which was capable of forming numerous hydrogen bonds. These bonds were instrumental in the interruption of the radical rebound reactions leading to the formation of α- and β-hydroxo fatty acids. Therefore, it was conjectured that an additional increase in the polarity of P450 OleT_JE’s active site would hold back the reactions that form hydroxylation products. Another amendment was appending electron-extracting moieties to the C_α or C_β locus to elevate the energy needed to form the C-O bond and increase the radical rebound barriers.

Substrate Docking Protocols

In conventional enzymatic reactions, the binding of a substrate to an enzyme prompts a conformational modification in the three-dimensional organization of the resultant enzyme-substrate complex. However, this reaction proceeds at a pace that is too fast to allow the crystallization of the analogous structure. Advances in technology, particularly molecular and computational docking procedures have made it possible to predict the orientations and loci of binding substrates. Docking procedures exploit basic data about the substrate and protein surface, for example, the types and configurations of atoms, atomic modifications, and polarity.

An online server, SwissDock, which is available at www.swissdock.ch, was used for this step. These data were likened to find the most appropriate lock-and-key pairs. The enzyme and substrates were tested in each probable orientation after which the energies for each alignment were worked out via MM methods. The possible enzyme-substrate complex was pinpointed by picking out the arrangement with the least energy. The Autodock software package was used in this process (Quesne et al. 2016).

The Addition of Hydrogen Atoms and Protein Groups to the Structure

The execution of geometrical optimizations was followed by the addition of hydrogen atoms to the protein structure in the PDB file. Several online programs and packages were beneficial in enhancing the detectability of the correct positions of hydrogen atoms. The addition of hydrogen atoms was determined by the oxidation states, pKa systems, and hybridization of the atoms.

Selection of Molecular Modelling Replicas

The energy bonds were minimized using the right field force before the conducting of QM/MM calculations. Energy minimization made it possible to achieve correct bond lengths and hybridization structures. Several field forces were available. However, since this project involved an enzyme, e-biochemical field force such as GROMOS, CHARMM, or AMBER was ideal for the process. The force field calculations were directed by the following equations.

………………………… 4

………………….5

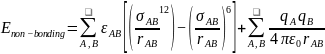…………….6

The first equation shows that MM energy (E_MM) is the aggregate of bonded and non-bonded interactions. In the above equations, d expresses the bond length, ϴ designates the angles of valence bonding and x symbolizes torsional dihedral angles. The dihedral attribute is a cosine function that considers the torsional multiplicity (n) and phase (δ) concerning a binding constant (k_x). The non-bonding energy between two atoms A and B is distributed between two interactions: a Lennard-Jones expression and a Coulomb interaction as shown in equation 6.

The Lennard-Jones expression consists of the r_AB term that identifies interatomic expanse, whereas ϵ_AB and σ_AB portray the depth, breadth, and size of the inactive well. On the other hand, the (q_Aq_B) term symbolizes the operational atomic charge of the two atoms A and B, whereas ϵ₀ designates permittivity in a vacuum. The value of q_Aq_B increases as the distance between the two atoms and ϵ₀ decreases.

Solvation of the Protein Structure

One inadequacy noted in the crystallized protein structures in PDB format was the lack of some of the water molecules that should normally be available. This insufficiency was attributed to the fact that the removal of water from protein suspensions was a pre-requisite to the crystallization of protein structures (Jindal & Warshel 2016). Therefore, it was mandatory to add water to the initial starting structure to re-solvate it and make a replica of a realistic enzyme model at room temperature (Liu et al. 2015; Piana et al. 2015).

Re-solvation also made better the in vivo and in vitro representation of polarity (Bellissent-Funel et al. 2015). The major limitation of available resolving methods was that it was difficult to add water molecules to the innermost regions of the protein. Besides, water molecules tend to leave behind pits in the boundary of the protein, which gets in the way with the calculations (Jindal & Warshel 2016). Therefore, it was necessary to conduct several re-solvation attempts of the system until the protein structure could not hold any more water molecules. Molecular, dynamic equilibration methods were used to transfer water molecules into the pits.

One method required conducting a long MD simulation while exerting pressure from the perimeters of the system to compel the conveyance of water into the center of the protein. The solvation process was followed by a confirmation of the positions of the additional water molecules to ascertain that no hydrogen bonds had been formed using atoms that were expected to play a role in the subsequent reaction pathway.

Heating, Equilibrating, and Conducting Molecular Dynamics Simulation on the Solvated Structure

MD simulations can only be conducted on a system whose temperatures have been raised to the expected reaction temperatures to equilibrate the complex. Consequently, the temperature of the system was elevated in stages at small intervals ranging from 0°K to 298°K. During this process, the applied force field was used to minimize the hydrogen atoms and solvent molecules. When the desired temperature was achieved, the protein backbone became flexible, which equilibrated the system.

At that point, MD simulations were run for 500 to 1000 picoseconds to generate snapshots of the protein structure, reaction intermediates, and products for the required QM/MM computations. Different temperatures were investigated to determine the impact of temperature on the decarboxylation mechanism of OleT_JE. An average of 6 simulations was done for each parameter.

Selection of Snapshots from the MD Simulation

It was necessary to choose several snapshots from the MD simulation because each snapshot was responsible for different computations in connection with the reaction rate, barrier height, and product formation. Furthermore, alterations in the patterns of hydrogen bonds within a single water molecule were likely to change the overall energy by approximately 4 kcal mol^-1 (Hayashi et al. 2017).

Therefore, taking some snapshots made it possible to examine different conformations of the protein. Numerous MD snapshots were taken from various points down the MD path graph. Each recreation was taken as the starting point for the creation of reaction profiles. Also, snapshots from diverse protein milieus had varying parameters, for example, local minima of comparative energies, spin-state gaps, and order. Therefore, the mean of the findings was obtained when assessing reaction schemes from more than one snapshot.

Selection of the QM Region, QM Methods, and Basis Set

The choice and size of the QM region affect the energetics of a reaction path and the electronic configuration of the active enzyme (Kulik et al. 2016; Karelina & Kulik 2017). Selecting a small QM region can lead to wrong descriptions of the polarisation of the system (Jindal & Warshel 2016). On the contrary, extremely large QM regions can result in excessive polarisation. Incongruences in bond lengths when relating QM regions of varying sizes are responsible for these observations. Therefore, it was necessary to examine several QM regions of assorted sizes to find out consistencies and select the correct regions.

Electrostatic and Mechanical Embedding Methods

Calculations of energies in the QM region should take into account the charges in the MM zone. Consequently, electrostatic or mechanical-embedding systems were helpful in this endeavor. The mechanical-embedding procedures determined van der Waals forces and electrostatic influences of the MM atoms in the QM zone (Jindal & Warshel 2016). The QM and MM energies were separated using geometric parameters such as the expanse of van der Waals interactions. Thereafter, the QM/MM expressions were assimilated directly into the force field estimations.

Calculation of QM/MM Energies

QM/MM energies were calculated by completing geometrical optimizations on the QM and MM zones. Two methods of optimization were possible: adiabatic and diabatic (Barbatti et al. 2014; Duarte et al. 2015; Cabeza de Vaca, Acebes & Guallar 2016).

The adiabatic geometry optimization approach entailed relaxing the macro element exchanges inside the QM core as well as the micro-component interactions brought about by the neighboring MM environment. In contrast, the diabatic style included the freezing of the QM core region in the course of optimization of the MM environment and vice versa. Nevertheless, linker atoms interacted in the boundary of the two regions, which meant that the total QM/MM energy was not contributed by the QM and MM energies only. Hence, it was necessary to consider the impact of these interactions during the computations. These coupling terms are described by the following equation.

E_QM/MM= E_QM +E_MM+ E _border …….……………7

QM/MM computations can be achieved by assimilating an MM into a QM software package. In this project, the ORCA software was used for the computations. ORCA is a contemporary ab initio and DFT package that can execute geometry optimizations and to forecast many spectroscopic structures at various stages of theory. ORCA integrates advanced ab initio quantum chemical techniques that apply the configuration interaction and coupled-cluster techniques into its functionalities (Metz et al. 2014; Dohm, Spohr & Korth 2017). These calculations can be executed using additive and subtractive procedures as shown in equations 8 and 9.

E ^Whole_QM/MM = E ^Whole_MM + E _QM (I+L) – E_MM (I+L) …..8

E ^Whole_QM/MM = E ^Environment_MM + E _QM (I+L) + E ^Coupling_QM/MM ………9

The subtractive approach, which was used in the project, involved taking advantage of linker atoms (L) to conceal the inner subsystems. The E_QM (I + L) term represented the sum of the QM region (I) and linker atoms (L) at the QM level. Conversely, the E_MM (I + L) term denoted a similar calculation at the MM level. However, it was important to subtract the MM energy of the inner subsystem from the energy of the entire system (E ^whole _MM) to preclude the double tallying of energies. The main benefit of the subtractive method was that it did not need a QM/MM joining term (Duarte et al. 2015; Řezáč 2016; Roßbach & Ochsenfeld 2017; Cao & Ryde 2018). The findings of the QM/MM processes are presented and explained in the next chapter.

Soundness, Rigour, and Limitations of the Methods

To ensure the reliability of the entire procedure and the outcomes, the starting structure was obtained from the protein databank library available at www.rcsb.org. This resource is recognized among the best sources for published crystal structure data where published enzymatic crystal structure coordinates are kept and systematized. The accuracy of the subsequent procedures was ensured by scrutinizing the initial starting structure to ensure that no errors were present.

Additional modifications were also done to this structure as described in the methods section. The rationale or these modifications was to ensure that all essential components were in place before cutting down restrictions on the protein’s backbone to forestall improper folding (Quesne et al. 2016). Another precaution that was taken to ensure the rigor and soundness of the method was taking into account the energy changes of the QM and MM regions separately before considering the energy of the inclusive QM/MM. This procedure made it possible to identify any changes in the overall system that were not reflected in the individual QM and MM energies.

The only limitation associated with the method is the estimation of approximation of the Hamiltonian, which hampers DFT optimizations from getting precise energies such as those obtained by ab initio techniques. Moreover, DFT methods do not factor delocalization and static correlation errors, which may affect the accuracy of the energies. However, the impact of this limitation was minimized by performing combined QM/MM modeling.

The procedure used in the entire experiment followed the schematic representation indicated in Figure 7. This procedure has been validated in various QM/MM experiments conducted by Zeida et al. (2014) and Wang et al. (2014). Zeida et al. (2014) used experimental means to show demonstrate the oxidative reaction mechanism of the enzyme peroxiredoxin from Mycobacterium tuberculosis AlphE. Through QM/MM techniques, it was established that the enzyme reduced hydrogen peroxide at a rate constant of 8.2×10^-4 m^-1 s^-1, which was consistent with a rate-determining activation barrier of 5.7 kcal mol^-1 (Zeida et al. 2014).

Nonetheless, it was observed that this reaction was too fast to permit the implementation of accurate kinetic studies using flow methodology. Therefore, QM/MM methods obtained theoretical activation energy of 4.8 kcal mol^–1. This difference was attributed to the impact of the environment on the energy profile. However, the experimental value had a close resemblance to the theoretical value, which validated the protocol.

On the other hand, Wang et al. (2014) used a similar approach to look into the enzyme machinery in the repair of exocyclic etheno bridge damage in adenine DNA

bases. The authors used QM/MM computations to investigate the repair machinery involved in the mending of the etheno-bridged adenine. This repair process was conducted by AlkB enzymes, particularly iron(IV)-oxo species. The theoretical energy barrier for the rate-determining step as 18.6 kcal mol^–1, whereas the experimental rate-limiting barrier, was shown to be 21 kcal mol^–1. These findings also indicate the dependability of the QM/MM technique.

Results and Discussion

This section gives a brief description and insight into how the DFT model optimization was used to prove the probability of a specific reaction pathway that uses the OleT enzyme to optimize the yield of terminal olefins over side products. Important information shows the potential energy of the system concerning effective parameters such as electronegativity interactions, length, and angle of bonds was methodically gathered using Orca. The utilization of Orca combined with the Chemcraft software provided a good visualization of the result files, representing optimization of transition state scans and potential energy in graphical illustrations.

There was no relevant experimental data to benchmark the study’s DFT model against. The choice of the coordinates of the starting crystal structure that corresponded with the structural homology of the OleT was very important to achieve reliable geometry optimization using the DFT technique in Orca software. Usually, these are taken from the protein data bank library (Blaszczyk et al. 2016). The heme model was simplified by removing the protonates and other side chains where the iron-coordinating cysteine was replaced with simplified SH and hexanoic acid, which was used as a substrate. One amino acid was included as a salt-bridge within the substrate. This simplification was used because it gave a good representation of the reaction and hastened the rate of the reaction.

Initially, the study focused on the change in geometry and configuration of the electrons of Cpd II in different spin states including quintet and triplet. Subsequently, an investigation was done on the abstraction of the hydrogen atom barrier energy from alpha carbon and beta carbon from the substrate to produce a hydrocarbon where Cpd II was in different spin states (quintet and triplet).

The abstraction of a Hydrogen Atom from the Alpha Carbon

The geometry of the reactant complex (RC) in the triplet and quintet spin states as well as their transition state was done when abstracting a hydrogen atom from the alpha carbon. The first optimization of the RC geometry was done in the quintet spin state, whereas the second optimization was done in the triplet spin state. Both optimizations were done at the UB3LYP level of theory.

This set basis was chosen based on the findings of previous extensive studies done on different basis sets via DFT to reveal the best set basis. The studies compared the findings with experimental data as references to reproduce experimental activation energy. It was noted that the B3LYP and PBE0 were the best to reproduce reliable experimental values (Coskun, Jerome & Friesner 2016; Costa et al. 2018; Friesner & Jerome 2017; Reinhard, Faponle & de Visser, 2016).

After the optimization of the RC, the geometry scan was made followed by the optimization of the transition state for the abstracting closet hydrogen from the alpha-carbon and beta-carbon positions. Another scan was made for the decarboxylation stage, once on the triplet and quintet states while putting a constraint on carbons 17, 18, 19, and 20 to keep them in the right orientation concerning the protein.

The outcomes from the optimization of the RC in the different states are illustrated in Tables 1 and 2 as well as Figures 10 to 12.

Table 1: Optimised r-bond length and angle for the RC in the triplet and (quintet) spin states. Alpha carbon optimized RC in the triplet state (total charge= 0).

To find the transition state (using the triplet spin state as an example and doing the same for quintet spin state), the first geometry scan for bond formation (H_α(52)-O₄₆) was done when one coordinate was fixed, and all the rest allowed to move freely. The resultant geometry shown in Figure 10 was produced. In the energy profile in Figure 11, the starting point of the scan indicates the reactants, whereas the endpoint is the reaction intermediates. The maximum point was subjected to a transition state and used as a starting point for the optimization of the transition state. Figure 12 represents the optimized transition state.

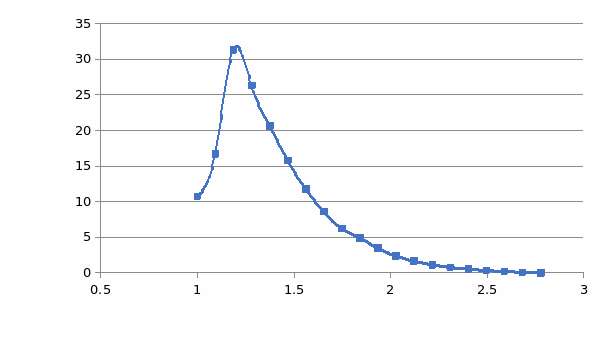
Table 2: Optimised geometry of the transition state (triplet spin state) following the abstraction of hydrogen from Cα.

Tables 1 and 2 indicate that there are minor differences in geometry optimization between ³RC and ⁵RC as well as between optimized ³TS and ⁵TS in the case of H-atom abstraction from the C_α position. Therefore, more attention was paid to the change of geometry between ³RC and ³TS. There were geometry differences between optimized ^TRC (reactant complex in the triplet spin state) and its optimized transition state to give an intermediate as shown in Tables 1 and 2. It was noted that some bond lengths increased while others decreased. The bond length between iron and oxygen in Cpd II (r_{Fe17 – O46}) in optimized ³RC was 1.76399 A.

However, this bond length was increased to 2.01426 A. The increase was due to the formation of another bond with the alpha hydrogen (H_α(52)-O₄₆) whose bond length was 3.34047 A. In the optimized RC case, it dropped significantly to 1.18046 A to produce the transition state, which also influenced the bond length of (r H₇₆ – O₄₈) that increased from 1.63252 A to 1.78520 A. Besides, the bond length of H₅₅ – O₄₆ decreased sharply from 5.10307A to 3.75557 A because of the presence of beta and alpha bonds that usually become stronger and shorter.

However, the rC₅₀ – C₅₃ bond increased slightly to 1.51590 A because of free electrons in the alpha carbon, which increased the strength of the bond between alpha carbon C50 and C49 thereby resulting in a decrease in bond length by about 0.02 A. Consequently, the bond between C49 and O48 became weaker and increased slightly from 1.30451 A to 1.30602 A. this increase was also because of the double bond between C49 and O47.

The bond length between beta carbon and H55 becomes longer by 0.00007 A due to a stronger attraction between alpha carbon and beta carbon. In the case of ^TRC, the angle between O₄₆ –C₅₃ –H₅₅ was 123.467°. This angle was reduced in the optimized transition state in the same spin state by about 33° due to a drop in the repulsion force between hydrogen atoms, which was attributed to the abstraction of the alpha hydrogen atom.

The differences in bond angles and lengths following the abstraction of a hydrogen atom is attributed to the effect of electron configurations. An electron configuration is the dispersion of electrons in an atom. Covalent bond formation entails the sharing of electrons between two or more atoms, which is an energy-requiring process. H-atom abstraction entails the breaking of bonds, which is also an energy-requiring process. The degree of the enthalpy barriers in H-atom removal differs from the outline and size of the cyclical transition state as well as the extent of substitution at the carbon and nitrogen atoms involved (Parab et al. 2018).

It has been shown that abstraction of hydrogen from tertiary carbons, ionized primary amines, transition states with chair-like shapes, and 1,5- or 1,6-abstraction have lower energy barriers, which explains why there were differences in hydrogen abstraction from the beta carbon differed in the triplet and quintet states (Jeffrey, Terrett & MacMillan 2015).

Validation of the Optimised Transition State of the Alpha Hydrogen Abstraction

Faponle, Quesne, and de Visser (2016) conducted studies on OleT_JE enzyme by abstracting hydrogen atoms from the alpha and beta carbons to produce olefins using QM/MM and DFT technique. This dissertation provides the optimized TS for abstracting H-atom from the alpha carbon position, which is relevant to the above work. Therefore, the findings of this study can be compared with the findings of de Visser et al. (2014).

The bond lengths of r _O-H, r _Fe-O and r _C-H were 1.297 (1.297), 1.780(1.767), and 1.320(1.314) respectively where the values in brackets represent abstracting hydrogen transition states by OleT_JE Cpd I from the alpha position of the substrate in the duplet spin state (²TS). On the other hand, the values without brackets show abstracting hydrogen transition states by OleT_JE Cpd I from the alpha position of the substrate in the quartet spin state (⁴TS) as described by de Visser et al. (2014).

In this study, the bond lengths of r _O-H (H_52(α) – O₄₆), r _Fe-O (Fe₁₇ – O₄₆), and r _C-H(C_50(α) – H₅₂) were 1.18046 (1.18254), 2.01426 (2.01527), and 1.41210 (14220) respectively. The bond distance values in brackets show the optimized geometry of the transition state in the quintet state, whereas values outside brackets represent the optimized geometry of the transition state in the triplet spin state. The differences between the findings of this project and those reported in the literature are 0.2 A or less except the bond length of r _Fe-O, which is slightly longer in this project by about 0.23 A. This difference is attributed to the oxygen atom (O46), which is linked to an iron atom bonded with two hydrogen atoms (one hydrogen atom is bonded with oxygen while the other is alpha hydrogen).

However, in the reviewed literature (de Visser et al. 2014), the oxygen was bonded with alpha hydrogen only because the starting compound was Cpd I. Therefore, the starting material contributed to the shorter and stronger bond between iron and hydrogen as reported. Additionally, the system used was protonated and the substrate was longer (C21), whereas the system in this project was deprotonated and the DFT model was simpler to enable the scanning and optimization within the limited duration of the project (2 months). Nonetheless, the findings of this project corroborated those presented by de Visser et al. (2014) in all other aspects except the length of the r _Fe-O bond.

Table 3: IR in the triplet spin state (total charge= 0).

Validation of the Optimised Transition State of the Beta Hydrogen Abstraction

This section discusses the steps followed and the ensuing change in geometry when a hydrogen atom was abstracted from the beta carbon position in the substrate to produce a hydrocarbon product. The energy barrier for transition states with different spin states (triplet and quintet) was also determined. The first transition state was determined by running two sets of geometry scans on (H55-O46) for the triplet and quintet spin states (because the beta hydrogen was far from O46) as shown in Figures 13 and 14. Figure 13 is the first scan while Figure 14 is the second scan for the triplet spin state.

Figure 15 shows that the energy profile was not perfect. However, the profile improved and smoothened in Figure 16. After that, the maximum point from the second scan was used as the starting point for optimizing the transition state with alpha hydrogen abstraction as shown in Figure 12 in the previous sub-section.

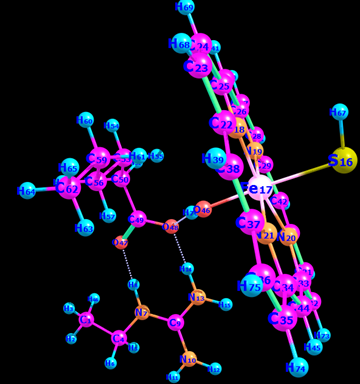
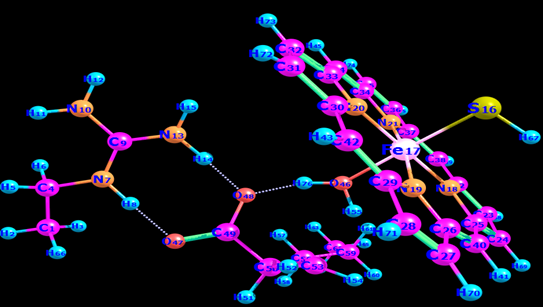
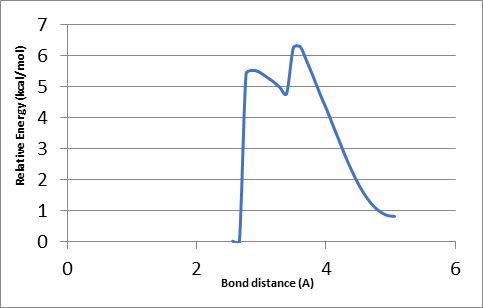
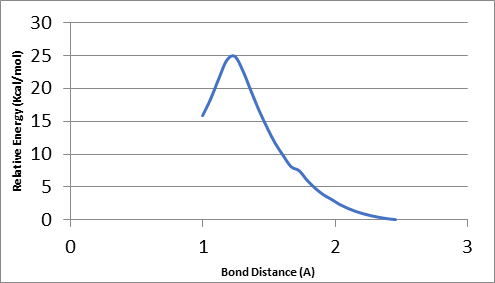
Optimized RC and First Transition State (Beta Hydrogen Abstraction)

Table 3 shows that there was no major difference in the geometry of the first transition state when abstracting hydrogen from the beta-carbon position when the spin state was triple or quintet. Additionally, there was no significant change in the geometry of optimized ³RC or ⁵RC. Consequently, the discussion here focused on comparing the change in geometry between the optimized ³RC and the initially optimized ³TS. The bond length of (Fe₁₇ – O₄₆) in ³TS (Tables 1 and 2) became weaker and longer by approximately 0.2 A.

This change was attributed to O46, which was bonded with two hydrogen atoms instead of one hydrogen atom as before in ⁵RC. The distance between the beta carbon C53 and its hydrogen H55 increased to 1.31656 A as a result of breaking the bond between them. Conversely, the distance between (H₇₆ – O₄₈) dropped slightly from 1.63252 A to 1.57364 A due to repulsion forces from beta hydrogen, which pushed the H76 towards O48. Furthermore, there was an increase in repulsion forces from the beta hydrogen (H55) that was expected to bond with O46 and push H52 (which was near O46) away from O46.

These repulsion forces resulted in an increase in the bond distance between O46 and H52 by 0.1 A. On the other hand, the bond length of (C₄₉ – O₄₈) increased slightly to 1.30637 A because of an increase in attraction forces between (H₇₆ – O₄₈). The beta carbon lost its hydrogen atoms leading to the presence of unpaired electrons hence an increase in repulsion forces, which caused the bond length between beta and alpha carbons (C₅₀ – C₅₃) to become shorter and tougher (1.52303A). Conversely, the bond length between alpha carbon and carbon 49 became weaker and longer by 0.01 A in the transition state. The angle of (O₄₆ –C₅₃ –H₅₅) reduced significantly by more than 100°, which confirmed that the transition state occurred at that point (Gudmundsson et al. 2014).

The optimized geometry of ³TS and (⁵TS) could be compared with Faponle, Quesne, and de Visser’s (2016) work where the bond length of r _O-H, r _Fe-O, and r _C-H were 1.272(1.404), 1.779(1.756), and 1.303(1.238) respectively.

The values in brackets represent the abstracting hydrogen transition states from the beta position of the substrate (Cpd I) by OleT_JE in the duplet spin state (²TS). On the other hand, the values outside brackets show the outcomes of the quartet spin state (⁴TS). The bond length values obtained in this project for (H_55(β) – O₄₆), (Fe₁₇ – O₄₆), and (C_53(β) – H₅₅) were 1.22057 A (1.22340), 1.89765 A(1.89766A), and 1.31656A (1.31766A) in the same order. These findings showed that there were no major differences between the geometry results obtained experimentally for r _O-H, r _C-H in this project, and those reported by Faponle, Quesne, and de Visser (2016).

In this project, there was a 4% decrease in the bond distance between the beta carbon and its abstracted hydrogen. However, the bond length between the alpha hydrogen and oxygen was approximately 1% more than that reported in the literature (Faponle, Quesne & de Visser (2016). The beta case in this project showed that the bond length was slightly higher than that reported in the literature by roughly 6.3%.

This observation was similar to the H-atom abstraction from the alpha carbon concerning the bond length (Fe-O). This discrepancy was attributed to the same reason mentioned in alpha hydrogen abstraction. Therefore, these comparisons point out the reliability of the results in this project even though non-protonated structures, a simplified model, and a shorter substrate (C6) were used, which indicated that these parameters do not have a significant effect on the overall outcomes.

Table 4: The first transition state in the triplet and (quintet) states (total charge= 0).

Intermediate (IR) and Second Transition State

After finishing the first transition state (³TS and ⁵TS), the geometries of ³IR and ⁵IR were optimized to prepare them for the decarboxylation transition state, which was done by running scan geometry on bond (C50-C49) in optimized ³IR and ⁵IR as shown in Figures 18 and 19. The maximum point from the energy profile in Figures 18 and 19 for these scans was used as the starting point for optimizing the ³TS and ⁵TS decarboxylation.

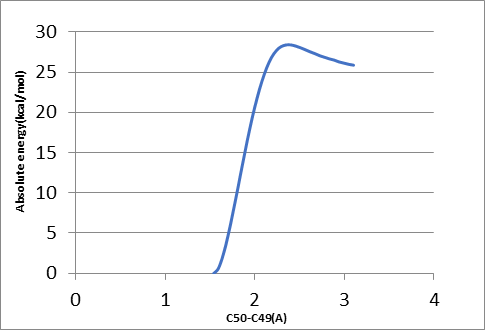
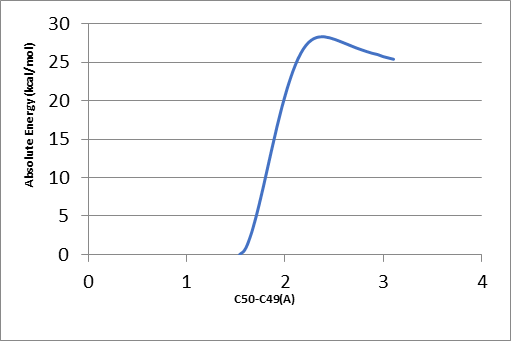
It was evident from Tables 5 and 6 that there were minimal differences in the optimized geometry of ³IR and ⁵IR, which were generated from the abstraction of a hydrogen atom from C_β and between optimized decarboxylation transition states on the triplet and quintet spin states (³TS_DE–_β and ⁵TS_DE–_β). As a result, this discussion concentrated on the change of geometry between ³IR and ³TS_DE–_β as examples.

First, the decarboxylation transition state had no notable effect on the bond length and angle of (O₄₆ –C₅₃ –H₅₅) in the intermediate product, particularly the bond length of (Fe₁₇ – O₄₆), (H₅₂ – O₄₆), (H₅₅ – O₄₆) and the average distance between iron atom and nitrogen atoms (Fe₁₇ – N). The formation of a double bond between C_β (C53) and C_α(C50) due to the decarboxylation process reduced the bond distance between them by about 9.1% and led to a slight reduction in the bond length between C49 and O48 by about 1.3%.

Table 5: Optimised transition state 2 (decarboxylation) for the triplet and (quintet) spin states.

Table 6: ³IR and (⁵IR).

Comparison Between Hydrogen Atom Abstraction from the Alpha Carbon and Beta Carbon Positions

This section investigated the differences between the reaction mechanism and energy barriers between the abstraction of a hydrogen atom from C_α and C_β pathways by Cpd II in the triplet and quintet spin states. To facilitate the comparisons, the ³RC was used as the reference state of relative energy for all phases ⁵RC, ³TS-_α,³IR-_α, ⁵TS-_α, ⁵IR-_α, ³TS1-_β, ³IR1-_β, ⁵TS1-_β, ⁵IR1-_β, ³TS_DE–_β ,³IR_DE–_β, ⁵TS_DE–_β, and ⁵IR_DE–_β as shown in below in Table 7.

Environmental factors exerted strong effects on the relative energy of ^3,5TS-_α, particularly interactional forces of H-bonding (de Visser 2016). After abstracting a hydrogen atom from either the alpha or beta carbon, a radical intermediate IR-_α or IR-_β was formed, which included Fe(3)-H₂O elements and a radical substrate on either the alpha or beta carbon positions. ^3,5IR-_α couldn’t proceed to the decarboxylation reaction after abstracting a hydrogen atom from C_α because the reaction required a high energy (ΔG>40 kcal/mol, which could not happen at room temperature) to move an additional hydrogen atom from beta carbon to the alpha carbon.

Consequently, ^3,5 IR-_α returned to the original reactants or stayed in the middle. Table 7 and the landscape in Figure 26 show that the beta carbon pathway leads to carboxylation products via two transition state TS1-_β and TS_DE–_β, which are generated from two radical intermediate IR1-_β and IR_DE respectively. On the contrary, the alpha carbon pathway leads to either the formation of the original reactants through transition states TS-_α produced from IR-_α (radical intermediate) or a compound that is in the middle of the reactants and intermediate.

However, the energy barrier of abstracting a hydrogen atom from C_α for the spin state 3 route reaction via IR-_α was slightly lower (by 4.7 Kcal/mol) than that on spin state 5. In contrast, the abstraction of a hydrogen atom from the C_β pathway reaction required an energy barrier for the spin state 3 paths through IR1-_β, which was significantly lower than the energy on spin state 5 by 13.5 Kcal/mol.

Nevertheless, there was no major difference in the H-atom transfer energy barrier between triplet and quintet states in the case of the C_β reaction mechanism because the activation barriers of the decarboxylation stages for both were nearly similar with values of 26.6 and 26.4 Kcal/mol respectively. Therefore, it was noted that the overall reaction to produce olefins via Cpd II and C_β pathway on the triplet spin state was limited and slowed down by the decarboxylation transition state, which had a higher energy barrier with a value of 26.6 kcal/mol compared to the first transition state that was used for the abstraction of a hydrogen atom, which had an energy barrier of 20.9 Kcal/mol (for its IR as a reference).

On the other hand, in the case of the quintet state, the rate-determining step for the overall reaction was the abstraction of a hydrogen-atom from C_β, which required activation energy of 34.4 Kcal/mol (concerning its IR). Therefore, the overall reaction needed to produce hydrocarbons via the C_β pathway on the triplet spin state would be slower than that on the quintet state due to a higher energy barrier required to transfer a hydrogen atom from the substrate to Cpd II in the triplet spin state (34.4 Kcal/mol).

The decarboxylation transition state, which can occur just after the abstraction of a hydrogen atom from beta carbon either on spin state 3 or 5 (³TS_DE–_β or ⁵TS_DE–_β) could be validated by a previous study done by Faponle et al. (2016) who used a DFT model to calculate the decarboxylation transition state via Cpd I on spin states 4 and 2. The values recorded by Faponle et al. (2016) were 6.7 (8.4) and 0.3(≈0) for where the values in bracket indicate S_n300 and those outside brackets indicate S_n400 (all values in Kcal/mol). However, in this project, these values were much higher in spin states 3 or 5 with a value of about 26 Kcal/mol.

However, even though different substrates were used in the literature and this project, the overall findings corroborate the observation that the lowest barriers of reaction were found in Cpd I as opposed to Cpd II. Nevertheless, those obtained via Cpd II were possible at room temperature considering the method and model (Postils et al. 2018). Consequently, this was a good indicator of the validity of the results.

Table 7: Relative energies in Kcal/mol of various reactants and transition states.

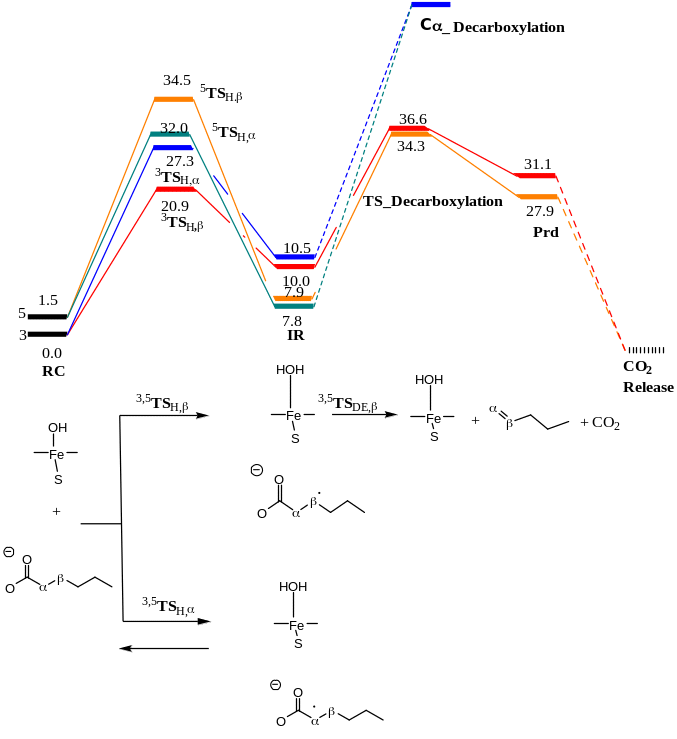
Conclusion

Overall, this study investigated and gave a deep insight into the reaction mechanism to increase the yield of olefins via the engineering OleT enzyme via Cpd II in the catalytic cycle of the enzyme using a simplified DFT model and QM/MM methodologies. This investigation started with the abstraction of a hydrogen atom from C_α and C_β positions via Cpd II on the triplet and quintet spin states. It was found that there were no major differences in the geometries of ³TS and ⁵TS when a hydrogen atom was abstracted from C_α or C_β positions.

However, comparing the energy differences between the abstraction of a hydrogen atom from C_α and C_β to produce their intermediates revealed minor differences in the transition state barrier energy between ³TS and ⁵TS. The abstraction from ⁵TS had higher barrier energy than ³TS. This study reported that the production of olefins from the alpha carbon either via Cpd II or Cpd I was unreasonable due to the high decarboxylation energy barrier. On the other hand, the production of hydrocarbon from the beta carbon either by Cpd I or Cpd II was feasible because the energy barrier of decarboxylation was reasonable. Moreover, the decarboxylation transition state via Cpd I was significantly lower notwithstanding the spin state.

The decarboxylation transition state through the abstraction of a hydrogen atom via the C_β route showed that the decarboxylation activation barrier for the triplet or quintet spin states were almost equal. Interestingly, the rate of the overall reaction mechanism on the quintet spin state was limited by the hydrogen atom abstraction energy barrier, which was attributed to the bond between hydrogen and C_β that was shorter and stronger. In the triplet spin state, the overall reaction rate was governed by the decarboxylation activation energy barrier. Considering that the triplet and quintet spin states had roughly similar decarboxylation transition barriers, it was concluded that the overall reaction rate to increase olefin yield was faster on the triplet state due to the relatively lower transition state for hydrogen abstraction from C_β.

Shortcomings and Future Recommendations

Addressing the Limitations to DFT models

The estimation of the Hamiltonian gets in the way of obtaining precise energies through DFT optimizations as opposed to using ab initio methods. Besides, DFT methods do not account for delocalization and static correlation inaccuracies, which leads to inaccurate energies. Therefore, it would be necessary to carry out combined QM/MM modeling and compare the outcomes with DFT optimizations to enhance the insight into reaction pathways. Future studies could consider using various larger basis sets, including G3Large and cc-pVTZ for DFT calculations to enhance precision.

Addressing the Effect of Substrate on Decarboxylation Reactions

In this project, a C6 substrate was used, whereas previous studies had used longer substrates. It has been shown that OleT enzyme has varying affinities for different fatty acid substrates, thereby leading to diverse conversion rates of the substrates to terminal olefins. Future studies could consider replicating the steps conducted in this project using different fatty acid substrates to determine the substrate with the best conversion rate using the proposed reaction machinery.

Reference List

Alolyan, I & Simos, TE 2015, ‘A high algebraic order multistage explicit four-step method with vanished phase-lag and its first, second, third, fourth and fifth derivatives for the numerical solution of the Schrödinger equation’, Journal of Mathematical Chemistry, vol. 53, no. 8, pp. 1915-1942.

Barbatti, M, Ruckenbauer, M, Plasser, F, Pittner, J, Granucci, G, Persico, M & Lischka, H 2014, ‘Newton‐X: a surface‐hopping program for nonadiabatic molecular dynamics’, Wiley Interdisciplinary Reviews: Computational Molecular Science, vol. 4, no. 1, pp. 26-33.

Belcher, J, McLean, KJ, Matthews, S, Woodward, LS, Fisher, K, Rigby, SE, Nelson, DR, Potts, D, Baynham, MT, Parker, DA & Leys, D 2014, ‘Structure and biochemical properties of the alkene producing cytochrome P450 OleTJE (CYP152L1) from the Jeotgalicoccus sp. 8456 bacterium’, Journal of Biological Chemistry, vol. 289, no. 10, pp. 6535-6550.

Beller, HR, Lee, TS & Katz, L 2015, ‘Natural products as biofuels and bio-based chemicals: fatty acids and isoprenoids’, Natural Product Reports, vol. 32, no. 10, pp. 1508-1526.

Bellissent-Funel, MC. Hassanali, A, Havenith, M, Henchman, R, Pohl, P, Sterpone, F, van der Spoel, D, Xu, Y & Garcia, AE 2016, ‘Water determines the structure and dynamics of proteins’, Chemical Reviews, vol. 116, no. 13, pp. 7673-7697.

Blaszczyk, M, Kurcinski, M, Kouza, M, Wieteska, L, Debinski, A, Kolinski, A & Kmiecik, S 2016, ‘Modeling of protein–peptide interactions using the CABS-dock web server for binding site search and flexible docking’, Methods, vol. 93, pp. 72-83.

Cabeza de Vaca, I, Acebes, S & Guallar, V 2016, ‘Ecoupling server: a tool to compute and analyze electronic couplings’, Journal of Computational Chemistry, vol. 37, no. 18, pp. 1740-1745.

Calbo, J, Orti, E, Sancho-García, JC & Arago, J 2015, ‘Accurate treatment of large supramolecular complexes by double-hybrid density functionals coupled with nonlocal van der Waals corrections’, Journal of Chemical Theory and Computation, vol. 11, no. 3, pp. 932-939.

Cao, L & Ryde, U 2018, ‘On the difference between additive and subtractive QM/MM calculations’, Frontiers in Chemistry, vol. 6, pp. 1-15.

Carvalho, AKF, da Conceição, LRV, Silva, JPV, Perez, VH & de Castro, HF 2017, ‘Biodiesel production from Mucor circinelloides using ethanol and heteropolyacid in one and two-step transesterification’, Fuel, vol. 202, pp. 503-511.

Chen, B, Lee, DY & Chang, MW 2015, ‘Combinatorial metabolic engineering of Saccharomyces cerevisiae for terminal alkene production’, Metabolic Engineering, vol. 31, pp. 53-61.

Chen, X, Zhou, L, Tian, K, Kumar, A, Singh, S, Prior, BA & Wang, Z 2013, ‘Metabolic engineering of Escherichia coli: a sustainable industrial platform for bio-based chemical production’, Biotechnology Advances, vol. 31, no. 8, pp. 1200-1223.

Choi, YJ & Lee, SY 2013, ‘Microbial production of short-chain alkanes, Nature, vol. 502, no. 7472, pp. 571-574.

Chum, HL, Warner, E, Seabra, JE & Macedo, IC 2014, ‘A comparison of commercial ethanol production systems from Brazilian sugarcane and US corn’, Biofuels, Bioproducts and Biorefining, vol. 8, no. 2, pp. 205-223.

Cornish-Bowden, A 2014, Principles of enzyme kinetics, Elsevier, New York, NY.

Coskun, D, Jerome, SV & Friesner, RA 2016, ‘Evaluation of the performance of the B3LYP, PBE0, and M06 DFT functionals, and DBLOC-corrected versions, in the calculation of redox potentials and spin splittings for transition metal containing systems,’ Journal of Chemical Theory and Computation, vol. 12, no. 3, pp. 1121-1128.

Costa, R, Reta, D, Moreira, IDP & Illas, F 2018, ‘Post-B3LYP functionals do not improve the description of magnetic coupling in Cu (II) dinuclear complexes’, The Journal of Physical Chemistry A, vol. 122, no. 13, pp. 3423-3432.

Covert, T, Greenstone, M & Knittel, CR 2016, ‘Will we ever stop using fossil fuels?’ Journal of Economic Perspectives, vol. 30, no. 1, pp. 117-138.

de Visser, SP 2009, ‘Introduction to quantum behaviour – a primer,’ in RK Allemann & NS Scrutton (eds), Quantum tunnelling in enzyme-catalysed reactions, Royal Society of Chemistry, Cambridge, UK, pp. 18-35.

de Visser, SP, Quesne, MG, Martin, B, Comba, P & Ryde, U 2014, ‘Computational modelling of oxygenation processes in enzymes and biomimetic model complexes’, Chemical Communications, vol. 50, no. 3, pp. 262-282.

Dennig, A, Kuhn, M, Tassoti, S, Thiessenhusen, A, Gilch, S, Bülter, T, Haas, T, Hall, M & Faber, K 2015, ‘Oxidative decarboxylation of short‐chain fatty acids to 1‐alkenes’, Angewandte Chemie International Edition, vol. 54, no. 30, pp. 8819-8822.

Dohm, S, Spohr, E & Korth, M 2017, ‘Developing adaptive QM/MM computer simulations for electrochemistry’, Journal of Computational Chemistry, vol. 38, no. 1, pp. 51-58.

Duarte, F, Amrein, BA, Blaha-Nelson, D & Kamerlin, SC 2015, ‘Recent advances in QM/MM free energy calculations using reference potentials’, Biochimica et Biophysica Acta (BBA)-General Subjects, vol. 1850, no. 5, pp. 954-965.

Edmonds, AR 2016, Angular momentum in quantum mechanics, Princeton University Press, Princeton.

European Biomass Industry Association 2018, Bioethanol. Web.

Fang, B, Xu, H, Liu, Y, Qi, F, Zhang, W, Chen, H, Wang, C, Wang, Y, Yang, W & Li, S 2017, ‘Mutagenesis and redox partners analysis of the P450 fatty acid decarboxylase OleT JE’, Scientific Reports, vol. 7, p. 44258.

Faponle, AS, Quesne, MG & de Visser, SP 2016, ‘Origin of the regioselective fatty‐acid hydroxylation versus decarboxylation by a cytochrome P450 Peroxygenase: what drives the reaction to biofuel production?’ Chemistry-A European Journal, vol. 22, no. 16, pp. 5478-5483.

Friesner, RA & Jerome, SV, 2017, ‘Localized orbital corrections for density functional calculations on transition metal containing systems’, Coordination Chemistry Reviews, vol. 344, pp. 205-213.

Fu, WJ, Chi, Z, Ma, ZC, Zhou, HX, Liu, GL, Lee, CF & Chi, ZM 2015, ‘Hydrocarbons, the advanced biofuels produced by different organisms, the evidence that alkanes in petroleum can be renewable’, Applied Microbiology and Biotechnology, vol. 99, no. 18, pp. 7481-7494.

Genheden, S, Reymer, A, Saenz-Méndez, P & Eriksson, LA 2017, ‘Computational chemistry and molecular modelling basics’, Computational Tools for Chemical Biology, vol. 3, pp. 1-38.

Ghosh, A, Khanra, S, Mondal, M, Halder, G, Tiwari, ON, Saini, S, Bhowmick, TK & Gayen, K 2016, ‘Progress toward isolation of strains and genetically engineered strains of microalgae for production of biofuel and other value added chemicals: a review’, Energy Conversion and Management, vol. 113, pp. 104-118.

Grant, JL, Hsieh, CH & Makris, TM 2015, ‘Decarboxylation of fatty acids to terminal alkenes by cytochrome P450 compound I’, Journal of the American Chemical Society, vol. 137, no. 15, pp. 4940-4943.

Grant, JL, Mitchell, ME & Makris, TM 2016, ‘Catalytic strategy for carbon− carbon bond scission by the cytochrome P450 OleT’, Proceedings of the National Academy of Sciences, vol. 113, no. 36, pp. 10049-10054.

Gricman, L, Vogel, C & Pleiss, J 2014, ‘Conservation analysis of class‐specific positions in cytochrome P450 monooxygenases: functional and structural relevance’, Proteins: Structure, Function, and Bioinformatics, vol. 82, no. 3, pp. 491-504.

Grimme, S & Schreiner, PR 2018, ‘Computational chemistry: the fate of current methods and future challenges’, Angewandte Chemie International Edition, vol. 57, no. 16, pp. 4170-4176.

Gudmundsson, M, Kim, S, Wu, M, Ishida, T, Momeni, MH., Vaaje-Kolstad, G, Lundberg, D, Royant, A, Ståhlberg, J, Eijsink, VG & Beckham, GT 2014, ‘Structural and electronic snapshots during the transition from a Cu (II) to Cu (I) metal center of a lytic polysaccharide monooxygenase by X-ray photo-reduction’, Journal of Biological Chemistry, pp. 1-8.

Guo, M, Song, W & Buhain, J 2015, ‘Bioenergy and biofuels: history, status, and perspective,’ Renewable and Sustainable Energy Reviews, vol. 42, pp. 712-725.

Hammerer, L, Winkler, CK & Kroutil, W 2018, ‘Regioselective biocatalytic hydroxylation of fatty acids by cytochrome P450s’, Catalysis Letters, vol. 148, no. 3, pp. 787-812.

Harrison, P & Valavanis, A 2016, Quantum wells, wires and dots: theoretical and computational physics of semiconductor nanostructures, John Wiley & Sons, Hoboken, NJ.

Hayashi, S, Uchida, Y, Hasegawa, T, Higashi, M, Kosugi, T & Kamiya, M 2017, ‘QM/MM geometry optimization on extensive free-energy surfaces for examination of enzymatic reactions and design of novel functional properties of proteins’, Annual Review of Physical Chemistry, vol. 68, pp. 135-154.

Hendry, JI, Prasannan, CB, Joshi, A, Dasgupta, S & Wangikar, PP 2016, ‘Metabolic model of Synechococcus sp. PCC 7002: prediction of flux distribution and network modification for enhanced biofuel production’, Bioresource Technology, vol. 213, pp. 190-197.

Hsieh, CH & Makris, TM 2016, ‘Expanding the substrate scope and reactivity of cytochrome P450 OleT’, Biochemical and Biophysical Research Communications, vol. 476, no. 4, pp. 462-466.

Hsieh, CH, Huang, X, Amaya, JA, Rutland, CD, Keys, CL, Groves, JT, Austin, RN & Makris, TM 2017, ‘The enigmatic P450 decarboxylase OleT is capable of, but evolved to frustrate, oxygen rebound chemistry’, Biochemistry, vol. 56, no. 26, pp. 3347-3357.

International Energy Agency 2018, Global energy demand grew by 2.1% in 2017, and carbon emissions rose for the first time since 2014. Web.

Jeffrey, JL, Terrett, JA & MacMillan, DW 2015, ‘O–H hydrogen bonding promotes H-atom transfer from α C–H bonds for C-alkylation of alcohols’, Science, vol. 349, no. 6255, pp. 1532-1536.

Jensen, F 2017, Introduction to computational chemistry, John Wiley & Sons, Hoboken, NJ.

Ji, L, Faponle, AS, Quesne, MG, Sainna, MA, Zhang, J, Franke, A, Kumar, D, van Eldik, R, Liu, W & de Visser, SP 2015, ‘Drug metabolism by cytochrome P450 enzymes: what distinguishes the pathways leading to substrate hydroxylation over desaturation?’ Chemistry-A European Journal, vol. 21, no. 25, pp. 9083-9092.

Jindal, G & Warshel, A 2016, ‘Exploring the dependence of QM/MM calculations of enzyme catalysis on the size of the QM region’, The Journal of Physical Chemistry B, vol. 120, no. 37, pp. 9913-9921.

Jones, RO 2015, ‘Density functional theory: its origins, rise to prominence, and future’, Reviews of Modern Physics, vol. 87, no. 3, pp. 897-923.

Karelina, M & Kulik, HJ 2017, ‘Systematic quantum mechanical region determination in QM/MM simulation’, Journal of Chemical Theory and Computation, vol. 13, no. 2, pp. 563-576.

Koch, W & Holthausen, MC 2015, A chemist’s guide to density functional theory, John Wiley & Sons, Hoboken, NJ.

Kulik, HJ, Zhang, J, Klinman, JP & Martinez, TJ 2016, ‘How large should the QM region be in QM/MM calculations? The case of catechol O-methyltransferase’, The Journal of Physical Chemistry B, vol. 120, no. 44, pp. 11381-11394.

Le Roy, RJ 2017, ‘LEVEL: A computer program for solving the radial Schrödinger equation for bound and quasibound levels’, Journal of Quantitative Spectroscopy and Radiative Transfer, vol. 186, pp. 167-178.

Lennen, RM & Pfleger, BF 2013, Microbial production of fatty acid-derived fuels and chemicals, Current Opinion in Biotechnology, vol.24, no. 6, pp. 1044-1053.

Lewars, EG 2016, Computational chemistry: introduction to the theory and applications of molecular and quantum mechanics, Springer, New York.

Li, X & Frisch, MJ 2006, ‘Energy-represented direct inversion in the iterative subspace within a hybrid geometry optimization method’, Journal of Chemical Theory and Computation, vol. 2, no. 3, pp. 835-839.

Liakos, DG & Neese, F 2015, ‘Domain based pair natural orbital coupled cluster studies on linear and folded alkane chains’, Journal of Chemical Theory and Computation, vol. 11, no. 5, pp. 2137-2143.

Liang, Y, Wei, J, Qiu, X & Jiao, N 2018, ‘Homogeneous oxygenase catalysis’, Chemical Reviews, vol. 118, no. 10, pp. 4912-4945.

Liao, JC, Mi, L, Pontrelli, S & Luo, S 2016, ‘Fuelling the future: microbial engineering for the production of sustainable biofuels’, Nature Reviews Microbiology, vol. 14, no. 5, pp. 288-304.

Lin, FM, Marsh, ENG & Lin, XN 2015, ‘Recent progress in hydrocarbon biofuel synthesis: pathways and enzymes’, Chinese Chemical Letters, vol. 26, no. 4, pp. 431-434.

Liu, F, Luehr, N, Kulik, HJ & Martínez, TJ 2015, ‘Quantum chemistry for solvated molecules on graphical processing units using polarizable continuum models, Journal of Chemical Theory and Computation, vol. 11, no. 7, pp. 3131-3144.

Liu, Y, Wang, C, Yan, J, Zhang, W, Guan, W, Lu, X & Li, S 2014, ‘Hydrogen peroxide-independent production of α-alkenes by OleT JE P450 fatty acid decarboxylase’, Biotechnology for Biofuels, vol. 7, no. 1, p. 28.

Mardirossian, N & Head-Gordon, M 2017, ‘Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals’, Molecular Physics, vol. 115, no. 19, pp. 2315-2372.

Marisch, K, Bayer, K, Scharl, T, Mairhofer, J, Krempl, PM, Hummel, K, Razzazi-Fazeli, E & Striedner, G 2013, ‘A comparative analysis of industrial Escherichia coli K–12 and B strains in high-glucose batch cultivations on process-, transcriptome-and proteome level’, PloS One, vol. 8, no. 8, pp. 1-16.

Martins, AL, Wanke, P, Chen, Z & Zhang, N 2018, ‘Ethanol production in Brazil: an assessment of main drivers with MCMC generalized linear mixed models’, Resources Conservation and Recycling, vol. 132, pp. 16-27.

Mathews, J & Ardiyanto, A 2015, ‘Estimation of greenhouse gas emissions for palm oil biodiesel production: a review and case study within the Council Directives 2009/28/EC of the European Parliament’, Journal of Oil Palm Environment & Health, vol. 6, pp. 25-41.

Matthews, S, Belcher, JD, Tee, KL, Girvan, HM, McLean, KJ, Rigby, SE, Levy, CW, Leys, D, Parker, DA, Blankley, RT & Munro, AW 2017a, ‘Catalytic determinants of alkene production by the cytochrome P450 peroxygenase OleTJE’, Journal of Biological Chemistry, vol. 292, no. 12, pp. 5128-5143.

Matthews, S, Tee, KL, Rattray, NJ, McLean, KJ, Leys, D, Parker, DA, Blankley, RT & Munro, AW 2017b, ‘Production of alkenes and novel secondary products by P450 OleTJE using novel H₂O₂‐generating fusion protein systems’, FEBS Letters, vol. 591, no. 5, pp. 737-750.

Maxwell, P, Pendás, ÁM & Popelier, PL 2016, ‘Extension of the interacting quantum atoms (IQA) approach to B3LYP level density functional theory (DFT)’, Physical Chemistry Chemical Physics, vol. 18, no. 31, pp. 20986-21000.

McMahon, D 2013, Quantum mechanics demystified (2nd ed.), McGraw-Hill, New York, NY.

Medvedev, MG, Bushmarinov, IS, Sun, J, Perdew, JP & Lyssenko, KA 2017, ‘Density functional theory is straying from the path toward the exact functional’, Science, vol. 355, no. 6320, pp. 49-52.

Melander, M, Jónsson, EO, Mortensen, JJ, Vegge, T & García Lastra, JM 2016, ‘Implementation of constrained DFT for computing charge transfer rates within the projector augmented wave method’, Journal of Chemical Theory and Computation, vol. 12, no. 11, pp. 5367-5378.

Mendez-Perez, D, Herman, NA & Pfleger, BF 2014, ‘A desaturase gene involved in formation of 1, 14-nonadecadiene in Synechococcus sp. strain PCC 7002’, Applied and Environmental Microbiology, vol. 80, no. 19, pp. 6073-6079.

Metz, S, Kästner, J, Sokol, AA, Keal, TW & Sherwood, P 2014, ‘C hem S hell—a modular software package for QM/MM simulations’, Wiley Interdisciplinary Reviews: Computational Molecular Science, vol. 4, no. 2, pp. 101-110.

Mofijur, M, Rasul, MG, Hyde, J, Azad, AK, Mamat, R & Bhuiya, MMK 2016, ‘Role of biofuel and their binary (diesel–biodiesel) and ternary (ethanol–biodiesel–diesel) blends on internal combustion engines emission reduction’, Renewable and Sustainable Energy Reviews, vol. 53, pp. 65-278.

Mohebbi, A, Abbaszadeh, M & Dehghan, M 2013, ‘The use of a meshless technique based on collocation and radial basis functions for solving the time fractional nonlinear Schrödinger equation arising in quantum mechanics’, Engineering Analysis with Boundary Elements, vol. 37, no. 2, pp.475-485.

Munro, AW, McLean, KJ, Grant, JL & Makris, TM 2018, ‘Structure and function of the cytochrome P450 peroxygenase enzymes’, Biochemical Society Transactions, vol. 46, no. 1, pp. 183-196.

Nebert, DW, Wikvall, K & Miller, WL 2013, ‘Human cytochromes P450 in health and disease’, Philosophical Transactions of the Royal Society B, vol. 368, no. 1612, pp. 1-21.

Nelson, DR 2018, ‘Cytochrome P450 diversity in the tree of life’, Biochimica et Biophysica Acta (BBA)-Proteins and Proteomics, vol. 1866, no. 1, pp. 141-154.

Nicoletti, G, Arcuri, N, Nicoletti, G & Bruno, R 2015, ‘A technical and environmental comparison between hydrogen and some fossil fuels’, Energy Conversion and Management, vol. 89, pp. 205-213.

Ning, H & Simos, TE 2015, ‘A low computational cost eight algebraic order hybrid method with vanished phase-lag and its first, second, third and fourth derivatives for the approximate solution of the Schrödinger equation’, Journal of Mathematical Chemistry, vol. 53, no. 6, pp. 1295-1312.

Obot, IB, Macdonald, DD & Gasem, ZM 2015, ‘Density functional theory (DFT) as a powerful tool for designing new organic corrosion inhibitors. Part 1: an overview’, Corrosion Science, vol. 99, pp. 1-30.

Omnes, R 2018, The interpretation of quantum mechanics, Princeton University Press, Princeton.

Pai, ZP, Selivanova, NV, Oleneva, PV, Berdnikova, PV & Beskopyl’nyi, AM 2017, ‘Catalytic oxidation of α-alkenes with hydrogen peroxide to carboxylic acids in the presence of peroxopolyoxotungstate complexes’, Catalysis Communications, vol. 88, pp. 45-49.

Parab, PR, Heufer, KA & Fernandes, RX 2018, ‘Reaction kinetics of hydrogen atom abstraction from isopentanol by the H atom and HO 2˙ radical’, Physical Chemistry Chemical Physics, vol. 20, no. 16, pp. 10895-10905.

Piana, S, Donchev, AG, Robustelli, P & Shaw, DE 2015, ‘Water dispersion interactions strongly influence simulated structural properties of disordered protein states’, The Journal of Physical Chemistry B, vol. 119, no. 16, pp. 5113-5123.

Postils, V, Saint-André, M, Timmins, A, Li, XX, Wang, Y, Luis, J, Solà, M & de Visser, S 2018, ‘Quantum mechanics/molecular mechanics studies on the relative reactivities of compound I and II in cytochrome P450 enzymes’, International Journal of Molecular Sciences, vol. 19, no. 7, pp. 1-20.

Pulidindi, IN & Gedanken, A 2015, ‘Employing novel techniques (microwave and sonochemistry) in the synthesis of biodiesel and bioethanol’, in Z Fang, RL Smith & Qi, X (eds), Production of biofuels and chemicals with ultrasound, Springer, Dordrecht, pp. 159-185.

Quesne, MG, Borowski, T & de Visser, SP 2016, ‘Quantum mechanics/molecular mechanics modelling of enzymatic processes: caveats and breakthroughs,’ Chemistry–A European Journal, vol. 22, no. 8, pp. 2562-2581.

Reinhard, CFG, Faponle, AS & de Visser, SP 2016, ‘Substrate sulfoxidation by an iron (IV)-oxo complex: benchmarking computationally calculated barrier heights to experiment’, The Journal of Physical Chemistry A, vol. 120, no. 49, pp. 9805-9814.

Renault, H, Bassard, JE, Hamberger, B & Werck-Reichhart, D 2014, ‘Cytochrome P450-mediated metabolic engineering: current progress and future challenges’, Current Opinion in Plant Biology, vol. 19, pp. 27-34.

Rendic, S & Guengerich, FP 2014, ‘Survey of human oxidoreductases and cytochrome P450 enzymes involved in the metabolism of xenobiotic and natural chemicals’, Chemical Research in Toxicology, vol. 28, no. 1, pp. 38-42.

Řezáč, J 2016, ‘Cuby: an integrative framework for computational chemistry’, Journal of Computational Chemistry, vol. 37, no. 13, pp. 1230-1237.

Rosano, GL & Ceccarelli, EA 2014, ‘Recombinant protein expression in Escherichia coli: advances and challenges’, Frontiers in Microbiology, vol. 5, pp. 1-17.

Roßbach, S & Ochsenfeld, C 2017, ‘Influence of coupling and embedding schemes on QM size convergence in QM/MM approaches for the example of a proton transfer in DNA’, Journal of Chemical Theory and Computation, vol. 13, no. 3, pp. 1102-1107.

Saika, H, Horita, J, Taguchi-Shiobara, F, Nonaka, S, Ayako, NY, Iwakami, S, Hori, K, Matsumoto, T, Tanaka, T, Itoh, T & Yano, M 2014, ‘A novel rice cytochrome P450 gene, CYP72A31, confers tolerance to acetolactate synthase-inhibiting herbicides in rice and Arabidopsis’, Plant Physiology, vol. 16, no. 33, pp. 1232-1240.

Shahir, SA, Masjuki, HH, Kalam, MA, Imran, A & Ashraful, AM 2015, ‘Performance and emission assessment of diesel–biodiesel–ethanol/bioethanol blend as a fuel in diesel engines: a review’, Renewable and Sustainable Energy Reviews, vol. 48, pp. 62-78.

Sparta, M & Neese, F 2014, ‘Chemical applications carried out by local pair natural orbital based coupled-cluster methods’, Chemical Society Reviews, vol. 43, no. 14, pp. 5032-5041.

Wang, B, Usharani, D, Li, C & Shaik, S 2014, ‘Theory uncovers an unusual mechanism of DNA repair of a lesioned adenine by AlkB enzymes,’ Journal of the American Chemical Society, vol. 136, no. 39, pp. 13895-13901.

Wang, J & Zhu, K 2018, ‘Microbial production of alka (e) ne biofuels’, Current Opinion in Biotechnology, vol. 50, pp. 11-18.

Wang, W, Liu, X & Lu, X 2013, ‘Engineering cyanobacteria to improve photosynthetic production of alka(e)nes’, Biotechnology for Biofuels, vol. 6, no. 1, pp. 1-9.

Wang, Y, Lan, D, Durrani, R & Hollmann, F 2017, ‘Peroxygenases en route to becoming dream catalysts. What are the opportunities and challenges?’ Current Opinion in Chemical Biology, vol. 37, pp. 1-9.

Xu, H, Ning, L, Yang, W, Fang, B, Wang, C, Wang, Y, Xu, J, Collin, S, Laeuffer, F, Fourage, L & Li, S 2017, ‘In vitro oxidative decarboxylation of free fatty acids to terminal alkenes by two new P450 peroxygenases’, Biotechnology for Biofuels, vol. 10, no. 1.

Yanai, T, Fann, GI, Beylkin, G & Harrison, RJ 2015, ‘Multiresolution quantum chemistry in multiwavelet bases: excited states from time-dependent Hartree–Fock and density functional theory via linear response’, Physical Chemistry Chemical Physics, vol. 17, no. 47, pp. 31405-31416.

Zanger, UM & Schwab, M 2013, ‘Cytochrome P450 enzymes in drug metabolism: regulation of gene expression, enzyme activities, and impact of genetic variation’, Pharmacology & Therapeutics, vol. 138, no. 1, pp. 103-141.

Zargar, A, Bailey, CB, Haushalter, RW, Eiben, CB, Katz, L & Keasling, JD 2017, ‘Leveraging microbial biosynthetic pathways for the generation of ‘drop-in’ biofuels’, Current Opinion in Biotechnology, vol. 45, pp. 156-163.

Zeida, A, Reyes, AM, Lebrero, MC, Radi, R, Trujillo, M & Estrin, DA 2014, ‘The extraordinary catalytic ability of peroxiredoxins: a combined experimental and QM/MM study on the fast thiol oxidation step,’ Chemical Communications, vol. 50, no. 70, pp. 10070-10073.

Zhao, YJ, Cheng, QQ, Su, P, Chen, X, Wang, XJ, Gao, W & Huang, LQ 2014, ‘Research progress relating to the role of cytochrome P450 in the biosynthesis of terpenoids in medicinal plants’, Applied Microbiology and Biotechnology, vol. 98, no. 6, pp. 2371-2383.

Zhou, YJ, Hu, Y, Zhu, Z, Siewers, V & Nielsen, J 2018, ‘Engineering 1-alkene biosynthesis and secretion by dynamic regulation in yeast’, ACS Synthetic Biology, vol. 7, no. 2, pp. 584-590.