Introduction
In the next 20 years, fossil fuels will account for 75% of all new electric power generating capacity, and 60% of this is assumed to come in the form of gas-fired power plants. Thus, many companies in the electricity and natural gas industries are considering investments in such plants. At the same time, the restructuring of electricity and gas markets has brought price transparency in the form of easily available spot- and forward prices. This article offers an approach to analyze gas-fired power plant investments, using the information available on electricity and gas futures and forward markets.
A gas-fired power plant may be interesting not only from the point of view of meeting increased power demand. Consider a company owning an undeveloped gas field at a distance to major gas demand hubs. Most of the world’s gas reserves are in such a category of “stranded gas”. Building natural gas pipelines is very costly, and the unit costs of gas transportation decrease rapidly with the capacity of the pipeline. Thus, locating a gas-fired power plant at the end of a new pipeline, near electricity demand, improves the economy of scale in the transmission of natural gas.
The research question addressed here is that of an energy manager having an opportunity to build a gas-fired power plant. How high should electricity prices be compared to gas prices, before I start building the plant? Does it matter whether the plant is baseload, running whatever the level of electricity and gas prices, or peak load, running only when the electricity price is above the fuel cost? How does the opportunity to abandon the plant influence the decision to invest? How do greenhouse gas emission costs affect profitability?
Whether a new power plant will be run as a baseload plant or ramped up and down according to current energy prices, depends more on the state of the local natural gas market than the technical design of the plant itself. New gas plants will often be of combined cycle gas turbine (CCGT) type, which can be operated both as baseload and peak load plants. The operating flexibility is often constrained by the flexibility of the gas inflow. If there is little local storage and/or alternative uses of the natural gas, the plant operator will seldom find it profitable to ramp down the plant.
The energy price process
Seasonality in the supply and demand of electricity and natural gas, combined with limited storage opportunities, causes cycles and peaks in electricity and gas prices. Spark spread measures the contribution margin of a gas-fired power plant, thus it is defined as the difference between the price of electricity Se and the cost of gas used for the generation of electricity.
(1) S = Se – Kh Sg
Where Sg is the price of gas and heat rate Kh is the amount of gas required to generate one MWh of electricity. Heat rate measures the efficiency of the plant: the lower the heart rate, the more efficient the facility. The efficiency of a gas-fired power plant varies slightly over time and with the output level. Still, the use of a constant heat rate is considered plausible for long-term analyses Note that the value of the spark spread can be negative as well as positive.
Electricity and gas are often used for to same purposes, such as cooling and heating, and thus the seasonality in electricity and gas prices have similar characteristics.
Due to the similar characteristics, the seasonality in electricity and gas forward prices decays from the spark spread and thus the spark spread process does not have seasonality. The following assumption describes our dynamics for the spark spread process. Schwartz and Smith (2000) use similar price dynamics to evaluate oil-linked assets.
Assumption 1
The spark spread is a sum of short-term deviations and equilibrium price
(2) S(t) = χ(t) + ξ(t)
Where the short-term deviations χ(t) are assumed to revert toward zero following an Ornstein-Uhlenbeck process
(3) dχ(t) = -κ χ(t)d(t) + αx dBx(t)
The equilibrium price ξ(t) is assumed to follow an arithmetic Brownian motion process
(4) dξ(t) = µz d(t) + αzdBz(t)
where, κ, αz, and µz are constants. Bκ (t) and Bξ(t) are standard Brownian motions, with correlation þdt = dBx(t) d Bξ(t) and information Ft.
An increase in the spark spread attracts high-cost producers to the market putting downward pressure on prices. Conversely, when prices decrease some high-cost producers will withdraw capacity temporarily, putting upward pressure on prices. As these entries and exits are not instantaneous, prices may be temporarily high or low but will revert toward the equilibrium price ξ. The mean-reversion parameter κ describes the rate at which the short-term deviations χ are expected to decay. The uncertainty in the equilibrium price is caused by the uncertainty in fundamental changes that are expected to persist.
For example, advances in gas exploration and production technology, changes in the discovery of natural gas, improved gas-fired power plant technology, and political and regulatory effects can cause changes in the equilibrium price. Other studies where the two factors are interpreted as short- and long-term factors include, for example, Schwartz and Smith (2000), Ross (1997), and Pilipović (1998). Note that the decreasing forward volatility structure, typical for commodities, can be seen as a consequence of the mean-reversion in the spot prices (see, e.g., Schwartz, 1997).
Traditionally, log-normal distributions are used to model non-negative prices. Instead of modeling electricity and gas prices independently, we model their difference. Our spark spread dynamics do not follow from the difference of two log-normally distributed price processes, however, it has similar characteristics, namely, it can have negative and positive values. The following corollary expresses the distribution of the future spark spread values.
Corollary
When spark spread has dynamics given in (2)-(4), prices are normally distributed, and the expected value and variance are given by
(5) E[S(T)|Ft ] = e–κ(T-t) χ(t) + ξ(t) + µξ (T-t)
(6) Var(S(T)) = (α2/2κ) (1 – e-2κ(T-t) ) + α2ξ (T-t) + 2(1 – e–κ(T-t) ) þαxαξ/κ
Corollary states that the spark spread is a sum of two normally distributed variables: equilibrium price and short-term variations. The expected value of short-term variations converges to zero as the maturity T increases and thus the expected value of the spark spread converges to the expected value of the equilibrium price. The mean-reversion parameter describes the rate of this convergence. The maturity in which short-term deviations are expected to halve is given by
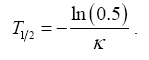
The spark spread variance caused by the uncertainty in the equilibrium price increases linearly as a function of maturity, whereas the spark spread variance due to the short-term variations converges towards α2/2κ.
Gas plant valuation
In this section, we calculate upper and lower bounds for the value of the gas-fired power plant. The following assumption gives the operational characteristics of the plant.
Assumption 2
The plant can be ramped up and down according to changes in the spark spread. The costs associated with starting up and shutting down the plant can be amortized into fixed costs.
In a gas-fired power plant, the operation and maintenance costs do not vary much over time, thus it is realistic to assume that the fixed costs are constant. The ramping policy of a particular plant depends on local conditions associated with plant design and gas inflow arrangement. Instead of giving an exact definition for the ramping policy, we use upper and lower bounds for the gains associated with ramping. The lower bound V can be calculated by assuming that the plant cannot exploit unexpected changes in the spark spread, i.e. by assuming that the plant produces electricity at the rated capacity independent of the spark spread. Such a plant is often called a baseload plant. The following lemma gives the value of a baseload plant.
An owner of a gas-fired power plant can react to adverse changes in the spark spread by temporarily shutting down the plant. Such a plant is often called a peak load plant. The value of a peak load plant is the discounted sum of expected spark spread values less emission and fixed costs plus the option value of being able to ramp up and down. The value of the up and down ramping is dependent on the response times of the plant and is maximized when ramping up and down can be done without delay. In other words, the upper bound V for the plant value can be calculated by assuming that the up and down ramping can be done without delay, i.e. by assuming that the plant produces electricity only when the spark spread exceeds emission costs.
Investment analysis
The following assumption characterizes the variables affecting the investment decisions.
Assumption 3
The investment decisions are made as a function of equilibrium price. In investment decisions, the lifetime of the plant is assumed to be infinite.
Assumption 3 states that when the gas plant investments, i.e. building and abandonment, are considered the decisions are made as a function of the equilibrium price ξ, i.e. the current short-term realization is omitted in investment decisions. The short-term dynamics, i.e. short-term volatility σχ and mean-reversion κ, still affect the value of the plant, and thus they also affect the investment decision. Thus, the short-term dynamics are important in the investment decision, even though the particular realization is assumed to be zero when investment decisions are made.
The omission of the short-term realization is motivated by the fact that gas-fired power plants are long-term investments, and a gas plant investment is never commenced due to a non-persistent spike in the price process. The assumption that investment decisions are made as a function of equilibrium price is a realistic approximation of the investment decision process if the expected lifetime of the short-term deviations is considerably smaller than the expected lifetime of the plant.
In Section 5 we use mean-reversion = 2.6, which gives, with, that the short-term variations are expected to halve in about three months. Usually, the lifetime of a gas-fired power plant is assumed to be around 30 years, and building a gas-fired power plant takes usually about two years. Thus, the approximation obtained by omitting the short-term realization in the investment decision is realistic. Note that in reality there can be exceptional peak periods when the mean-reversion towards equilibrium price is lower than usual.
Application
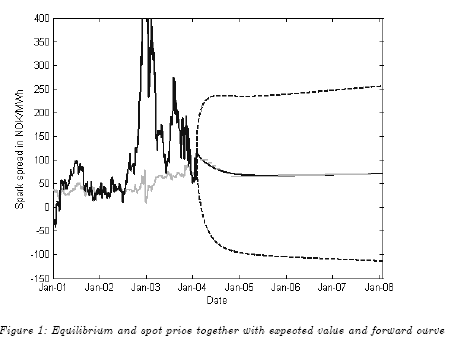
It is estimated that over the period 2001-2030 about 2000 GW of new natural gas-fired power plant capacity will be built (see, e.g., IEA, 2003). Our method can be used to analyze all these investments. In this example, we concentrate on the possibility to build a natural gas-fired power plant in Norway. The main reason to concentrate on this particular case is the availability of good spark spread and investment cost data. Norwegian energy and environmental authorities have given four licenses to build a gas-fired power plant and we take the view of an investor having one of these licenses.
The costs of building and running a natural gas-fired power plant in Norway are estimated by Undrum et al. (2000). With an exchange rate of 7 NOK/USD, a combined cycle gas turbine (CCGT) plant costs approximately 1620 MNOK, and the maintenance costs G are approximately 50 MNOK/year. We estimate that the costs of holding the license W are 5% of the fixed costs of running a plant. In Undrum et al. (2000) approximately 35% of the investment costs are used for capital equipment.
We assume that if the plant is abandoned all the capital equipment can be realized on the second-hand market, i.e. the salvage value of plant D is 567 MNOK. The estimated parameters are for a gas plant whose maximum capacity is 415 MW. We assume that the capacity factor of the plant is 90%, thus we use a production capacity of 3.27 TWh/year. Table 1 contains a summary of the gas plant parameters.

Conclusions
We use real options theory to analyze gas-fired power plant investments. Our valuation is based on electricity and gas forward prices. We have derived a method to compute upper and lower bounds for the plant value and investment thresholds when the spark spread follows a two-factor model, capturing both the short-term mean-reversion and long-term uncertainty.
In our case study, we take the view of an investor having a license to build a gas-fired power plant. Our results indicate that the abandonment option and the operating flexibility interact so that their joint value is less than their separate values because an option to permanently shut down compensates the option to temporarily shut down and vice versa. However, the case study indicates that the addition of the abandonment option does not dramatically change the bounds of the building threshold.
On the other hand, the difference in upper and lower bound of the investment thresholds is considerable and thus the operating flexibility has a significant effect on the building decision. Thus, when investments in gas-fired power plants are considered a good overall view of the investment problem can be made by ignoring the abandonment option, whereas the operating flexibility and time-to-build option should not be disregarded.
As a peak load plant operates only when the spark spread exceeds emission costs, the peak load plant, at time s, can be replicated with C European call options on the spark spread with a strike price equal to the emission costs E. At time t, the value of such an option, maturing at time s, is
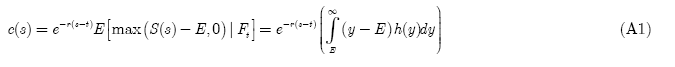
where is a normally distributed variable with mean and variance v. is the density function of a normally distributed variable y? The integration gives,
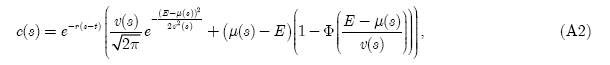
where is the normal cumulative distribution function? The value of a plant with lifetime ()Φ⋅T is given by,

which gives,
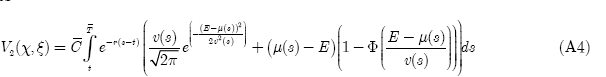
References
Deng, S.J., 2003, Valuation of Investment and Opportunity to Invest in Power Generation Assets with Spikes in Power Prices, Working paper, Georgia Institute of Technology.
Deng, S.J., B. Johnson, A. Sogomonian, 2001, Exotic electricity options and the valuation of electricity generation and transmission assets, Decision Support Systems, (30) 3, pp. 383-392.
Deng, S.J., S.S. Oren, 2003, Valuation of Electricity Generation Assets with Operational Characteristics, Probability in the Engineering and Informational Sciences, forthcoming.
Dixit, A.K., R.S. Pindyck, 1994, Investment under Uncertainty, Princeton University Press.
Ellerman, D., 1998, Note on the Seemingly Indefinite Extension of Power Plant Lives, A Panel Contribution, The Energy Journal 19 (2), pp. 129-132.
Fama, E.F., K. French, 1987, Commodity futures prices: Some evidence on forecast power, premiums, and the theory of storage, Journal of Business 60 (1), pp. 55-73.
Harvey, A. C., 1989, Forecasting, Structural Time Series Models and the Kalman Filter, Cambridge University Press, Cambridge, U.K.