Relationship between the variables
The dependent variable in the model will be the rate of growth of GDP while the independent variable is the amount of investment expressed as a percentage of GDP. A sample data for ten countries will be used to estimate the regression equation.
The regression line will take the form g = b0 + b1 (1/Yi) + ui when the ordinary least squares method is used. The regression line can be simplified to Y = b0 + b1X
Y = rate of growth of GDP
X = Investment
The theoretical expectations are b0 can take any value and b1 > 0.
Regression Results
From the above table, the regression equation can be written as Y = 0.3319 + 0.1863X. The intercept value of 0.3319 shows the proportion of growth in GDP that is not dependent on investment.
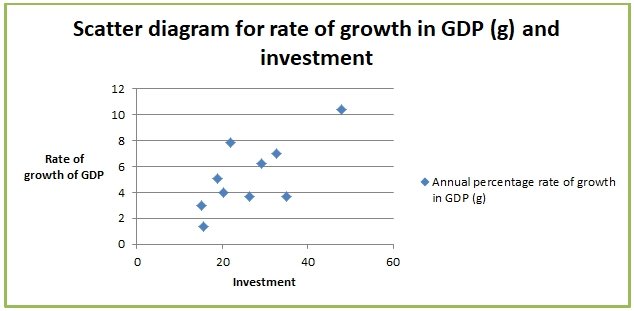
The value captures the variables that were not included in the regression analysis. The coefficient value is 0.1863. The sign is positive which implies that there is a positive linear relationship between growth in GDP and investment. An increase in investment by one unit leads to the growth in GDP by 0.1863 units. This can be shown by the scatter diagram shown below (Bazen, 96).
Evaluation of regression model
Evaluation of the regression model can be done by testing the statistical significance of the variables. Testing statistical significance shows whether the amount of investment is a significant determinant of the rate of change of GDP. A t – test will be used since the sample size is small. A two tailed t- test is carried out at 95% level of confidence.
Null hypothesis: Ho: bi = 0
Alternative hypothesis: Ho: bi ≠ 0
The null hypothesis implies that the variables are not significant determinants of demand. The alternative hypothesis implies that variables are significant determinant of demand. The table below summarizes the results of the t – tests.
From the table above, the t – value of the y – intercept (0.1858) is less than the computed value of t (1.9432). Thus, the null hypothesis will not be rejected. This implies that the intercept is not a significant determinant of the rate of growth of GDP a 95% significance level and thus can be dropped. On the other hand, the t – value of the coefficient of the slope (2.9244) is greater than the values of t – tabulated (1.9432).
Therefore, the null hypothesis will be rejected and this implies that the investment a significant explanatory variable. Thus, investment is statistically significant at the 95% level of significance. The value of the intercept is not relevant when testing the significance of the regression variables. Since the explanatory variable is statistically significant, it implies that the regression line can be used for prediction.
R-square value
Coefficient of determination shows the amount of changes in the dependent variable that are explained by the independent variables. A high coefficient of determination implies that the explanatory variables adequately explain the variations in the rate of growth of GDP.
A low value of coefficient of determination implies that the explanatory variables do not explain the variations in the rate of growth of GDP adequately. For this regression, the value of R2 is 51.67%. This implies that the amount of investment explains only 51.67% of the variation in rate of growth of GDP. It is an indication of a weak explanatory variable.
The value of adjusted R2 is superior to the value of the R2 since it eliminates the effects of the number of variables used in the regression model. It is because the number of variables has an effect of increasing the value of R2. Also, the value of adjusted R2 is low at 46.63%.
The value is quite low and it indicates that the regression model is weak. It is worth mentioning that the value of adjusted R2 is not always superior in all cases. The value is of significance only when dealing with a sample not a whole population as in the case above. Besides, it is also relevant in model building (Verbeek 87).
Testing the overall significance of the regression model
The overall significance of the regression model can be analyzed using an F – test at the 95% level of confidence.
Null hypothesis H0: β0 = β1 =, = βp
Alternative hypothesis H1: βj ≠ 0, for at least one value of j
The table below summarizes he results of F – test for the regression equation.
From the table above, the value of F – computed is greater than the value of F – tabulated. Thus, the null hypothesis will be rejected and conclude that the overall regression line is significant.
How to improve the model and results
First, the manager can remove the variables that are found not to be statistically significant. Also, the manager can improve the regression equation by more adding variables which are considered that can affect the regression equation. This is often done at the formulation stage. Finally, the manager can increase the power of the explanatory variables. Thus, the management can either use cubic or quadratic functions.
Theoretical Framework Justification
Human Capital Theory
Fringe benefits and wage earnings are identified as the main components of compensation summation. However, fringe benefits are apportioned a larger share in the total compensation matrix due to the fact that their influence was experiencing a consistent growth over the last decade in the labor market.
These fringe benefits are classified as social security, unemployment compensation and employee’s compensation for every unit of labor given as indicated in the human capital theory. In classification, these fringe benefits assume the form of insurance benefits, paid leave, and legally acquired benefits to a worker for every unit of labor delivered against the revenue realized (Allen 10).
Labor Market Discrimination Theory
Type and form of fringe benefits are never universal. Rather, they are influenced by the type of industry in which labor operates, ration and occupational groups as indicated in the labor market discrimination theory. This is due to the fact that governments and other agencies have introduced laws and regulations aimed at pushing for higher and reliable compensation. In most instances, the blue collar employees have a larger share of the legalities, construed benefits than their counterparts in white collar jobs (Verbeek 77).
Job Characteristics Theory
In a bid to extrapolate this relationship, the Job Characteristics/Compensating Wage Differentials theory is a certain reason for the experienced growth over the sample space. Reflectively, the variables interacting within the parameters of this theory are leisure and income within the normal indifference curve.
Consequently, the resulting interaction becomes flexible to different bundles of budget constraints that might be present at each level of computation. Further, this theory asserts that indifference curve is a product of various fringe benefits and wage rates that interact simultaneously to yield same utility level for each worker. When all other factors are held constant, higher swing of the indifference curve indicates higher levels of utility (Kanbur 87).
Incentive pay theory
The requirement for intrinsic substitution as a component of the decision science aimed at managing the fringe benefits are peculiar in labor economics. In such case, the foregone alternative would be forfeiting leisure related savings for health and pension needs which are characterized as basic for every worker.
The adoption of this thought is influenced by the fact that basic needs are more critical than the secondary wants in the matrix of fringe benefits. Besides, the long term effects of purchasing the basic needs are greater than those opting to acquire secondary needs upfront. Tax advantages to employers, scale of economies, and efficiency are major factors that led to the growth of fringe benefits (Koning 137). Therefore, as fringe benefits increase, the workers’ utility increased in the same ratio.
Labor Union
When implanting compensation plans, it is important for the firm to consider the efficiency of each labor unit against the wage payments. These units should be quantified in line with performance targets and revenue accrued. In order to achieve this, introduction of regulatory agents, such as supervisors who work alongside the employees may be beneficial.
As explained in the labor union theory, this agent often influences wage prices to be very sticky downwards. In the sample, the unionized employees reported stable income and structured employment contracts as pull factors into their respective fields.
Regression analysis
The regression line can be simplified to take the form Y = b0 + b1X + b2X + …+ bnX for n variables.
Y = rate of growth of GDP
Xi = All explanatory variables
Evaluation of regression model
A two tailed t- test is carried out at 95% level of confidence.
Null hypothesis: Ho: bi = 0
Alternative hypothesis: Ho: bi ≠ 0
The table below summarizes the results of the regression and a determination a test on whether they are significant or not.
From the table above, only three variables are statistically significant. All the others are not at the 95% level of confidence and thus can be dropped from the regression model.
R-square value
The value of R2 is 27.8%. This implies that the amount of investment explains only 51.67% of the variation in rate of growth of GDP. It is an indication of a weak explanatory variable. Also, the value of adjusted R2 is low at 26.1%. The value is quite low and it indicates that the regression model is weak. More variable statistically significant variables should be added to the regression model at the formulation stage (Allen 97).
Testing the overall significance of the regression model
The overall significance of the regression model can be analyzed using an F – test at the 95% level of confidence.
Null hypothesis H0: β0 = β1 =, = βp
Alternative hypothesis H1: βj ≠ 0, for at least one value of j
The table below summarizes he results of F – test for the regression equation.
From the table above, the value of F – computed is greater than the value of F – tabulated. Thus, the null hypothesis will be rejected and conclude that the overall regression line is significant.
Test for autocorrelation
Autocorrelation is a scenario where the error terms of different periods are related. It is often tested either graphically or by use of the Durbin Watson test. The Durbin Watson lies between 0 and 4. A value of 2 implies that there is no correlation between the variables. A value of 0 and 4 indicates a strong correlation. The values are summarized below (Kanbur 77).
The information in the table below shows that there is no serial correlation in the data.
Heteroscedasticity
Heteroscedasticity is a scenario where the error term violates the assumption of constant variance. The standard error of the regression equation is 6920.717929. In the regression above, the robust standard errors are 8859.92728. It is an indication of the possible existence of heteroscedasticity (Koning 98).
Works Cited
Allen, Michael. Understanding Regression Analysis, Alabama: Springer, 2004. Print.
Bazen, Stephen. Econometric Methods for Labour Economics, Oxford: Oxford University Press, 2011. Print.
Kanbur, Ravi. Labour Markets and Economic Development, Alabama: Routledge, 2012. Print.
Koning, Jaap. Evaluation of Active Labour Market Policies: Measures, Public Private Partnerships And Benchmarking, New York: Edward Elgar Publishing, 2007. Print.
Verbeek, Marno. A Guide to Modern Econometrics, New York: John Wiley & Sons, 2008. Print.