Introduction
Sampling may be defined as the process of selecting an appropriate representation of a population for the purpose of attaining information regarding the overall population. A sampling distribution may be defined as a probability distribution of all possible means of a given size selected from a population. A sample must be unbiased and representative for accurate results.
Sampling
Sampling methods may be broadly categorized into probability and non-probability methods. Probability sampling supports the idea that elements to be included in the sample have a non-zero (and known) chance.
They include random, systematic and stratified sampling. In non-probability sampling, population elements are selected in a non-random way such that elements do not have a known chance of being selected. They include judgemental, convenience, quota and snowball sampling.
Probability Sampling methods
Random sampling occurs when each element in the population has an equal chance of being selected to form part of the sample and selection relies on chance. Stratified sampling occurs where the population is divided into groups ensuring that elements within each group are as similar as possible.
This process is called stratification and the groups formed are called strata. Systematic sampling is used for quality control sampling. In this case, a sample element is enlisted as a member of the sample if it falls under the kth element. For example, for a population of 500, every tenth, twentieth or fiftieth element will be included.
Non-probability sampling
In judgemental sampling the researcher selects whom to include as the sample element with the belief that their views are fundamental for the study. For convenience sampling, selection of elements is done on the basis of convenience which may be time, cost or location.
In quota sampling the researcher initially identifies the strata within the population. After defining the strata, the researcher uses convenience or judgmental sampling to include elements in the sample. Snowball sampling uses referrals made by respondents which may be used by the researcher as part of the sample.
Sampling distributions
Sampling distributions consider the laws of probability. For example, a nanny has 5 children under her supervision.
These five children form the entire population i.e. n=5. Therefore the population mean is calculated by:
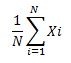
Hence,
µ= (2+4+6+8+10) /5= 6 years.
The standard deviation of the population is given by: (X- µ)2
∑ (X – µ)2= 40
Therefore σ = ![]() =2.83 Years
=2.83 Years
Taking all the possible random samples of size 2, we will get 10 possible such samples.
The grand mean of these samples is given by:
(3+4+5+6+….+8+9) ÷10= 6 years
The sampling distribution of the means of the ages is tabulated below and has two predictable patterns.
The sampling distribution gives a mean that is similar to the population mean.
E(ẋ)= ![]()
3(0.1)+4(0.1)+5(0.2)+6(0.2)+7(0.2)+8(0.1)+9(0.1)= 6 years
The shape of the sampling distribution is bell shaped even when the population is not normally distributed provided the sample is reasonably sufficient. This property leads to the central limit theorem which states that regardless of the shape of the distribution of the population, the distribution of the sample mean approaches the normal probability distribution as the sample size increases.
Standard error of the mean
This is a measure of dispersion of the distribution of the sample means and is similar in concept to the standard deviation in a frequency distribution. It measures the likely deviation of a sample mean from the grand mean of the sampling distribution. From the example of the five children, taking the sample means, we can calculate σ ẋ as:
σ ẋ = ![]()
where N is the number of sample means.
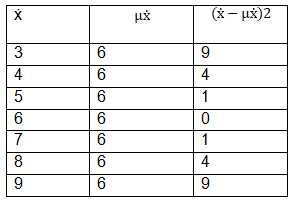
Hence
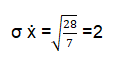
2 is the standard error of mean. This value will always be less than σ. The relationship between σ and σ ẋ is indicated below.
σ ẋ = ![]()
Standard normal distribution
Taking students with a mean µ of 120 and a standard deviation σ of 10, we can calculate the probability of any student chosen at random with scores between 120 and 125.
z= (ẋ – µ)/ σ
(125-120)÷10=0.5
The area of z = 0.5 from z tables is 0.1915 meaning there is a 19.15% chance that a student picked at random will have scores between 120 and 125.
Supposing that a random sample of 25 students is chosen, to find the probability that the mean sample will be between 120 and 125:
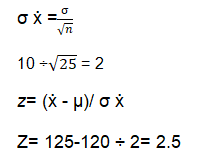
This indicates the standardized normal distribution of the means. The area for z= 2.5 is 0.4938 indicating that this is the probability that the sample mean will fall between 120 and 125.
Conclusion
In conclusion, sampling is used to provide a general feel of the population from which the researcher can make statistical inferences. Sampling distributions indicate the properties of the population in terms of how the data elements relate to each other. Accurate estimation depends on representativeness of the sample as well as extent of variability in the population.